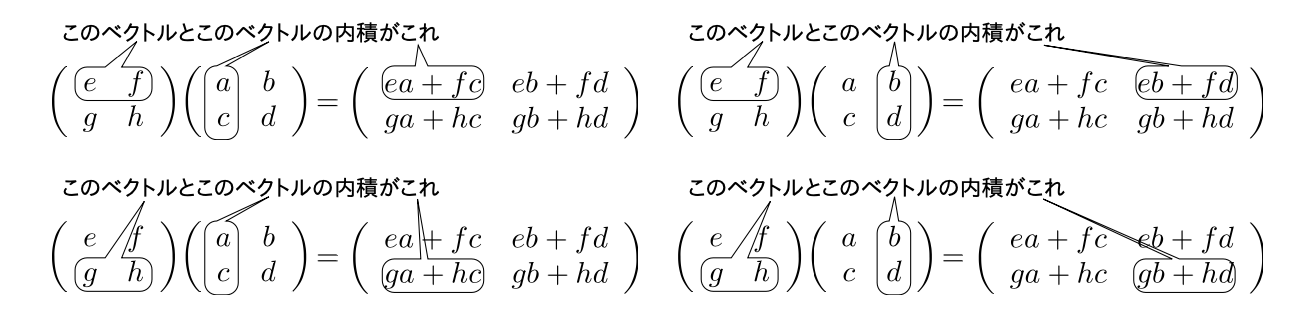行列の成分と演算
行列とその成分
行列の成分は
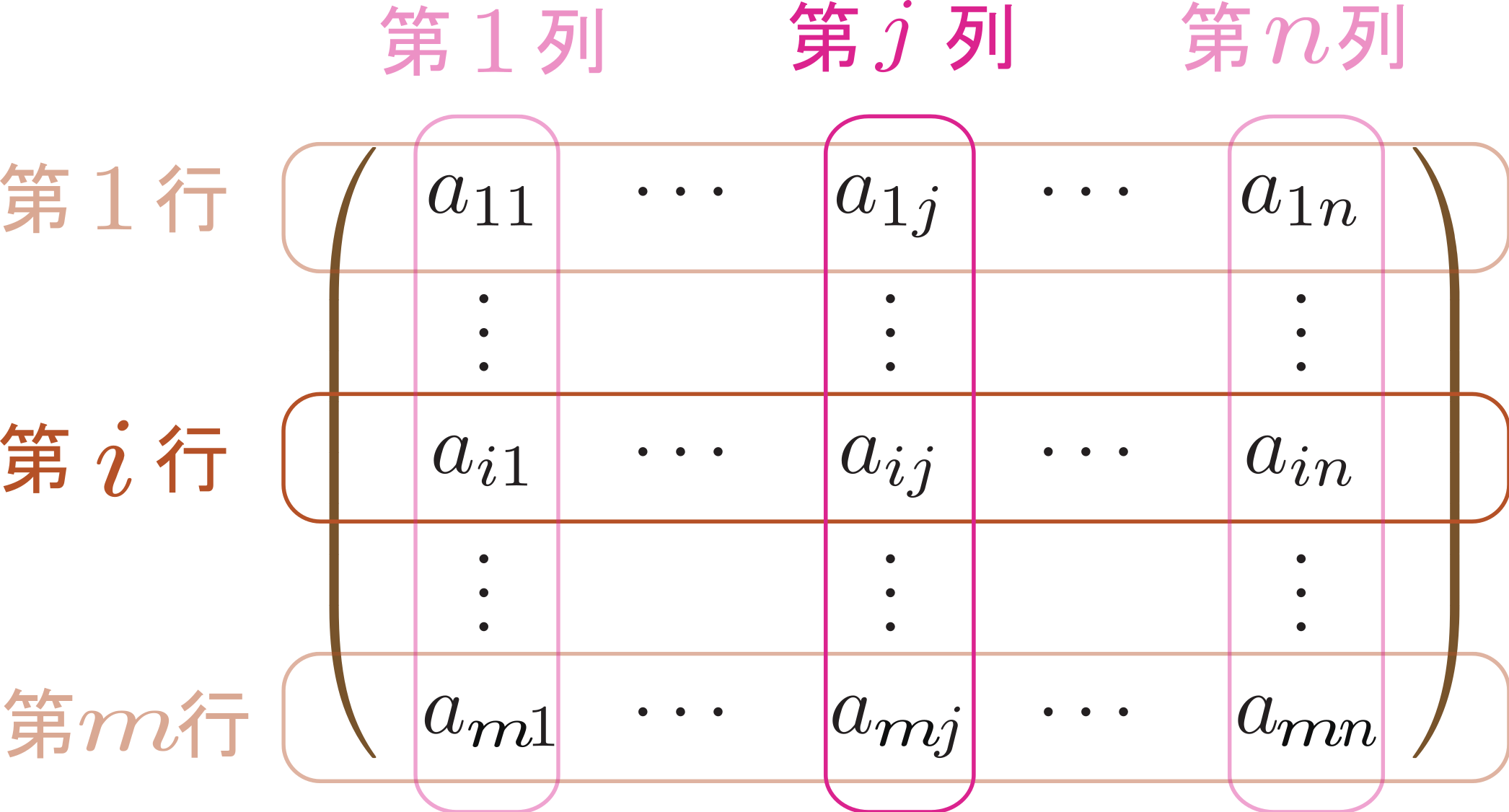
のように二つの添字をつけて「$i$行$j$列の成分」を$a_{ij}$と表すことにする。
縦に$n$行、横に$m$列の数字が並んでいる行列を「$n$行$m$列の行列」と呼ぶ。この行列は \begin{align} \mtx[c]{ \yokovectnashi{\begin{array}{cccc}a_{11}&a_{12}&\cdots&a_{1m}\end{array}}\\[2mm] \yokovectnashi{\begin{array}{cccc}a_{21}&a_{22}&\cdots&a_{2m}\end{array}}\\[2mm] \vdots\\ \yokovectnashi{\begin{array}{cccc}a_{n1}&a_{n2}&\cdots&a_{nm}\end{array}} } = \mtx[c]{ \nagayokovec{\vec W_1}\\ \nagayokovec{\vec W_2}\\ \vdots\\ \nagayokovec{\vec W_n} } \end{align} のように、「$m$成分の横ベクトルが$n$行並んでいる」と解釈することも、 \begin{align} \mtx[cccc]{ \tatevec{\begin{array}{c}a_{11}\\a_{21}\\\vdots\\a_{n1} \end{array}}& \tatevec{\begin{array}{c}a_{12}\\a_{22}\\\vdots\\a_{n1} \end{array}}& \cdots& \tatevec{\begin{array}{c}a_{1n}\\a_{22}\\\vdots\\a_{n1} \end{array}} }= \mtx[cccc]{\nagatatevec{\vec V_1}&\nagatatevec{\vec V_2}&\cdots&\nagatatevec{\vec V_m}} \label{tatevecnarabi} \end{align} のように、「$n$成分の縦ベクトルが$m$列並んでいる」と解釈することもできる。
上では、ベクトル$\mtx[cccc]{a_{i1}&a_{i2}&\cdots&a_{im}}$を$(\vec W_i)^t$と略記し、ベクトル$ \mtx[c]{a_{1j}\\a_{2j}\\\vdots\\a_{nj}}$を$\vec V_j$と略記した。つまり、$\vec W_i$は$\mtx[c]{a_{i1}\\a_{i2}\\\vdots\\a_{in}}$である($\vec V_i$と$\vec W_i$では足の付き方が違うことに注意。$\vec W$の方は上の式では転置した形で登場している)。こうして分割して考ると、行列の掛け算は \begin{align} \mtx[c]{\ycol{y_1}\\\ycol{y_2}\\\vdots\\\ycol{y_n}}= \mtx[cccc]{\nagatatevec{\vec V_1}&\nagatatevec{\vec V_2}&\cdots&\nagatatevec{\vec V_m}} \mtx[c]{\xcol{x_1}\\\xcol{x_2}\\\vdots\\\xcol{x_m}} = \vec V_1\xcol{x_1} +\vec V_2\xcol{x_2}+\cdots \vec V_m\xcol{x_m} \end{align} のように「$\allc{\vec V_*}$の線形結合」と考えることもできるし、 \begin{align} \mtx[c]{\ycol{y_1}\\\ycol{y_2}\\\vdots\\\ycol{y_n}} = \mtx[c]{ \nagayokovec{\vec W_1}\\ \nagayokovec{\vec W_2}\\ \vdots\\ \nagayokovec{\vec W_n} } \mtx[c]{\xcol{x_1}\\\xcol{x_2}\\\vdots\\\xcol{x_m}} = \mtx[c]{{\vec W_1}\cdot\xcol{\vec x}\\ {\vec W_2}\cdot\xcol{\vec x}\\ \vdots\\ {\vec W_n}\cdot\xcol{\vec x}\\ } \end{align} のように「それぞれの$\allc{\vec W_*}$との内積」と考えることもできる(どちらの見方も重要である)。
行列の演算:$2\times2$行列
連立1次方程式を解く
「連立1次方程式を解く」という計算を、一般の行列$\mtx{a&b\\c&d}$の場合で行ってみよう。すなわち、 \begin{eqnarray} \mtx[cc]{a&b\\c&d}\mtx[c]{\xcol{x}\\\ycol{y}}=&\mtx[c]{X\\Y} \end{eqnarray} を解く。まずは先に考えたように、行列を列ベクトルが並んでいるものと考えて、 \begin{align} \mtx[c]{a\\c}\xcol{x}+\mtx[c]{b\\d}\ycol{y}=\mtx[c]{X\\Y} \end{align} と書き直す。まず、「$\xcol{x}$を求めたいから$\ycol{y}$を消したい」と考える。そのためには、$\mtx{d&-b}$との内積を取ればよい(あるいは、$\mtx[c]{b\\d}$との外積を取ればよい)。結果は内積を使う計算なら \begin{align} \mtx{d&-b}\mtx[c]{a\\c}\xcol{x}+\gunderbrace{\mtx{d&-b}\mtx[c]{b\\d}}_{=0}\ycol{y}=\mtx{d&-b}\mtx[c]{X\\Y} \end{align} で、外積を使う計算なら \begin{align} \mtx[c]{b\\d}\times\mtx[c]{a\\c}\xcol{x}+\gunderbrace{\mtx[c]{b\\d}\times\mtx[c]{b\\d}}_{=0}\ycol{y}=\mtx[c]{b\\d}\times\mtx[c]{X\\Y} \end{align} であり、どちらにしても \begin{align} (ad-bc)\xcol{x}= dX-bY \end{align} である。同様に「$\ycol{y}$を求めたいから$\xcol{x}$を消したい」という動機のもと、$\mtx{-c&a}$との内積を取って(あるいは$\mtx[c]{a\\c}$との外積を取って)、 \begin{align} \gunderbrace{\mtx{-c&a}\mtx[c]{a\\c}}_{=0}\xcol{x}+\mtx{-c&a}\mtx[c]{b\\d}\ycol{y}=\mtx{-c&a}\mtx[c]{X\\Y} \end{align} または \begin{align} \gunderbrace{\mtx[c]{a\\c}\times\mtx[c]{a\\c}}_{=0}\xcol{x}+\mtx[c]{a\\c}\times\mtx[c]{b\\d}\ycol{y}=\mtx[c]{a\\c}\times\mtx[c]{X\\Y} \end{align} を得る。今出した二つの式は(まとめやすいので内積の方を使う) \begin{align} (ad-bc)\xcol{x}=&\mtx{d&-b}\mtx[c]{X\\Y}\\ (ad-bc)\ycol{y}=&\mtx{-c&a}\mtx[c]{X\\Y} \end{align} だからまとめて書くと \begin{align} \gunderbrace{(ad-bc)}_{=D}\mtx[c]{\xcol{x}\\\ycol{y}}=&\mtx{d&-b\\-c&a}\mtx[c]{X\\Y} \end{align} となる。
以上をベクトルの記号を使って$\vec v_1=\mtx[c]{a\\c},\vec v_2=\mtx[c]{b\\d},\vec X=\mtx[c]{X\\Y}$として書くと \begin{align} &元の式& \vec v_1\xcol{x}+\vec v_2\ycol{y}=&\vec X\\ &\vec v_2と外積&\vec v_2\times \vec v_1\xcol{x}+\gunderbrace{\vec v_2\times\vec v_2}_{=\vec 0}\ycol{y}=&\vec v_2\times \vec X\\ &\vec v_1と外積&\gunderbrace{\vec v_1\times \vec v_1}_{=\vec 0}\xcol{x}+\vec v_1\times \vec v_2\ycol{y}=&\vec v_1\times\vec X\\ &まとめて&\vec v_2\times \vec v_1\mtx[c]{\xcol{x}\\ \ycol{y}}=&\mtx[c]{\vec v_2\times \vec X\\\vec v_1\times\vec X} \end{align} と考えてもよい(今2次元なので外積の結果はスカラーであることに注意)。