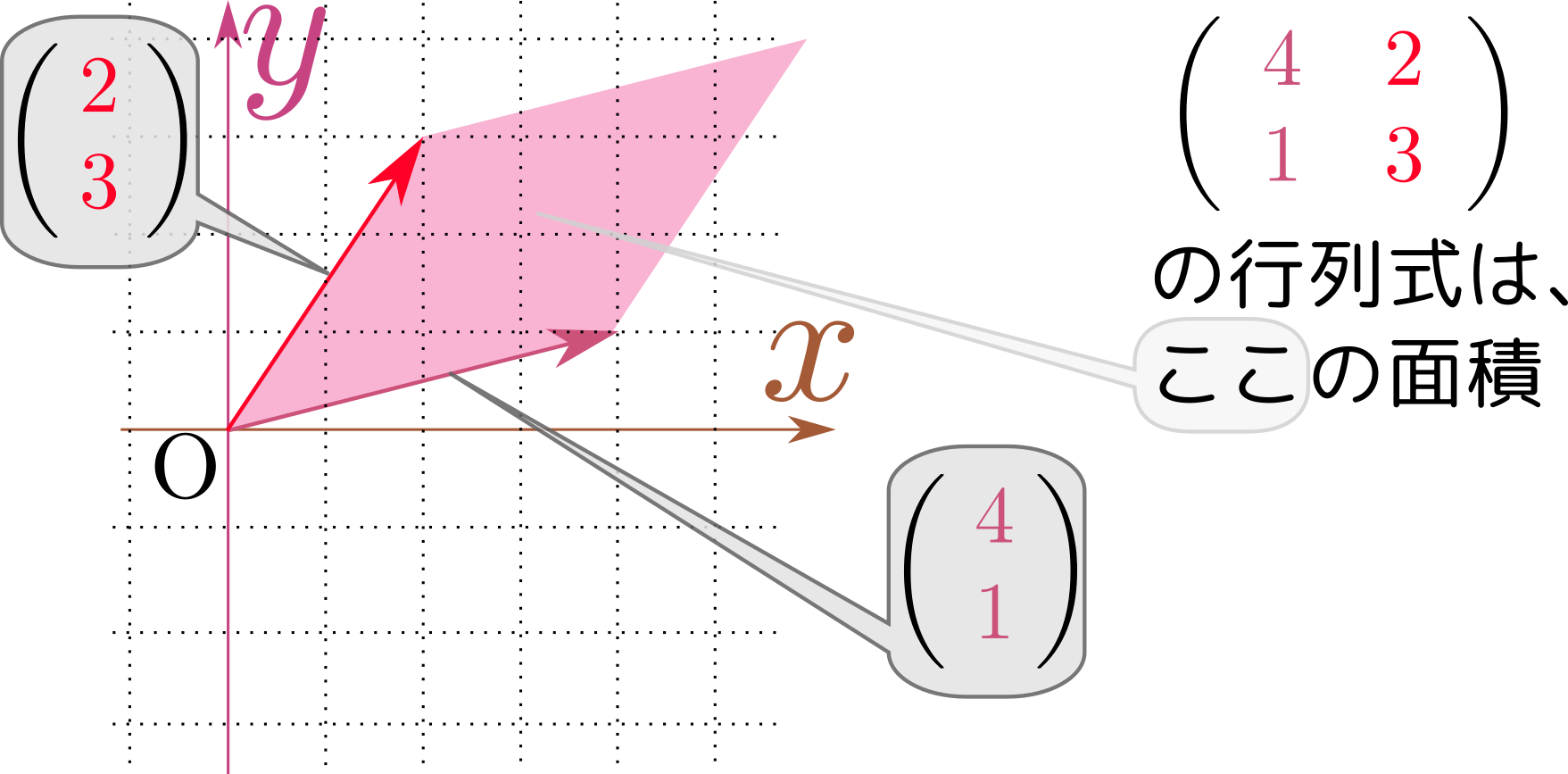
以下の説明ビデオは↓
ビデオと文章による説明を両方見て読んで、理解しておいてください。
$2\times2$行列の行列式には双線形性があったが、$3\times3$行列の行列式には「3重線形性」がある。すなわち、行列式を3本の列ベクトルの関数とみたとき、
\begin{align}
\det\mt{A}\kakko{\lambda_1\vec v_1^{(1)}+\lambda_2\vec v_1^{(2)},\vec v_2,\vec v_3}
=&
\lambda_1\det\mt{A}\kakko{\vec v_1^{(1)},\vec v_2,\vec v_3}
+\lambda_2\det\mt{A}\kakko{\vec v_1^{(2)},\vec v_2,\vec v_3}\\
\det\mt{A}\kakko{\vec v_1,\lambda_1\vec v_2^{(1)}+\lambda_2\vec v_2^{(2)},\vec v_3}
=&
\lambda_1\det\mt{A}\kakko{\vec v_1,\vec v_2^{(1)},\vec v_3}
+\lambda_2\det\mt{A}\kakko{\vec v_1,\vec v_2^{(2)},\vec v_3}\\
\det\mt{A}\kakko{\vec v_1,\vec v_2,\lambda_1\vec v_3^{(1)}+\lambda_2\vec v_3^{(2)}}
=&
\lambda_1\det\mt{A}\kakko{\vec v_1,\vec v_2,\vec v_3^{(1)}}
+\lambda_2\det\mt{A}\kakko{\vec v_1,\vec v_2,\vec v_3^{(2)}}
\end{align}
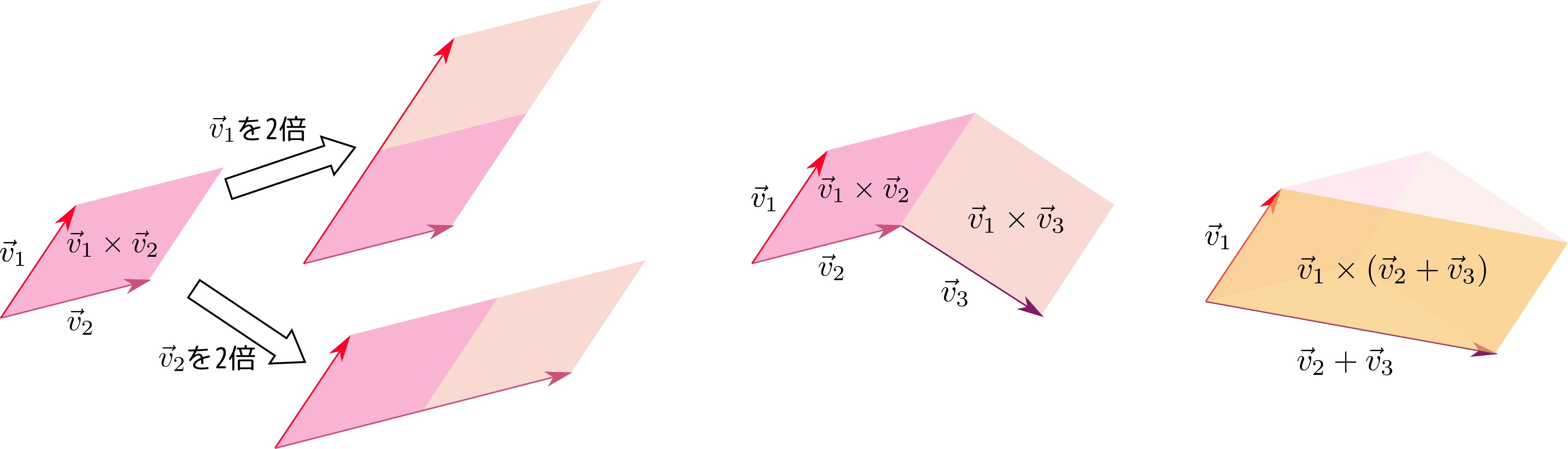
のように、どの引数に対しても線形性がある。また、$2\times2$同様に成り立つ式として、
\begin{align}
\det\mt{A}\kakko{\vec v_1,\vec v_2,\vec v_3+\lambda_1\vec v_1+\lambda_2\vec v_2}
= \det\mt{A}\kakko{\vec v_1,\vec v_2,\vec v_3}
\end{align}
という式、すなわち$\vec v_3$に他の2本のベクトルの線形結合を足しても、行列式の値は不変であるという式も成り立つ(上では3番目の引数つまり第3列について書いたが、第1列、第2列にも同様の式が成り立つ)。証明はレヴィ・チビタ記号を使うなら、
\begin{align}
\sum_{\dum[xcolor]{i},\dum[ycolor]{j},\dum[zcolor]{k}}\epsilon_{\dml[xcolor]{i}\dml[ycolor]{j}\dml[zcolor]{k}}A_{\dmr[xcolor]{i}1}A_{\dmr[ycolor]{j}2}\left(
A_{\dmr[zcolor]{k}3}
+\lambda_1A_{\dmr[zcolor]{k}1}
+\lambda_2A_{\dmr[zcolor]{k}2}
\right)
=\sum_{\dum[xcolor]{i},\dum[ycolor]{j},\dum[zcolor]{k}}\epsilon_{\dml[xcolor]{i}\dml[ycolor]{j}\dml[zcolor]{k}}A_{\dmr[xcolor]{i}1}A_{\dmr[ycolor]{j}2}A_{\dmr[zcolor]{k}3}
\end{align}
を示せばよい。
行列式が平行六面体の体積であるということを思い出すと、

のように「天井を平行移動させる」操作では体積が変わらないことに対応している。
$3\times3$の場合で、行列式を変えない行列の変形を見せるアプリがあるのでやってみて欲しい。
アプリの説明ビデオが↓
もう一つよく使われる性質は、列ベクトルの交換に関する反対称性
\begin{align}
\det\mt{A}\kakko{\vec v_1,\vec v_2,\vec v_3}
=- \det\mt{A}\kakko{\vec v_2,\vec v_1,\vec v_3}
=- \det\mt{A}\kakko{\vec v_1,\vec v_3,\vec v_2}
=- \det\mt{A}\kakko{\vec v_3,\vec v_2,\vec v_1}
\end{align}
とサイクリック置換で不変であること
\begin{align}
\det\mt{A}\kakko{\vec v_1,\vec v_2,\vec v_3}
= \det\mt{A}\kakko{\vec v_2,\vec v_3,\vec v_1}
= \det\mt{A}\kakko{\vec v_3,\vec v_1,\vec v_2}
\end{align}
である。これも証明は優しい(レヴィ・チビタ記号の性質からくる)。
行列式を行ベクトルの関数とみた場合も、上と同様の性質がある。それは、
\begin{align}
\sum_{\dum[xcolor]{i},\dum[ycolor]{j},\dum[zcolor]{k}}\epsilon_{\dml[xcolor]{i}\dml[ycolor]{j}\dml[zcolor]{k}}A_{\dmr[xcolor]{i}1}A_{\dmr[ycolor]{j}2}A_{\dmr[zcolor]{k}3}
=\sum_{\dum[xcolor]{i},\dum[ycolor]{j},\dum[zcolor]{k}}\epsilon_{\dml[xcolor]{i}\dml[ycolor]{j}\dml[zcolor]{k}}A_{1\dmr[xcolor]{i}}A_{2\dmr[ycolor]{j}}A_{3\dmr[zcolor]{k}}
\end{align}
が成り立つからである(二つの式で$A$の添字の付き方が逆であることに注意)。
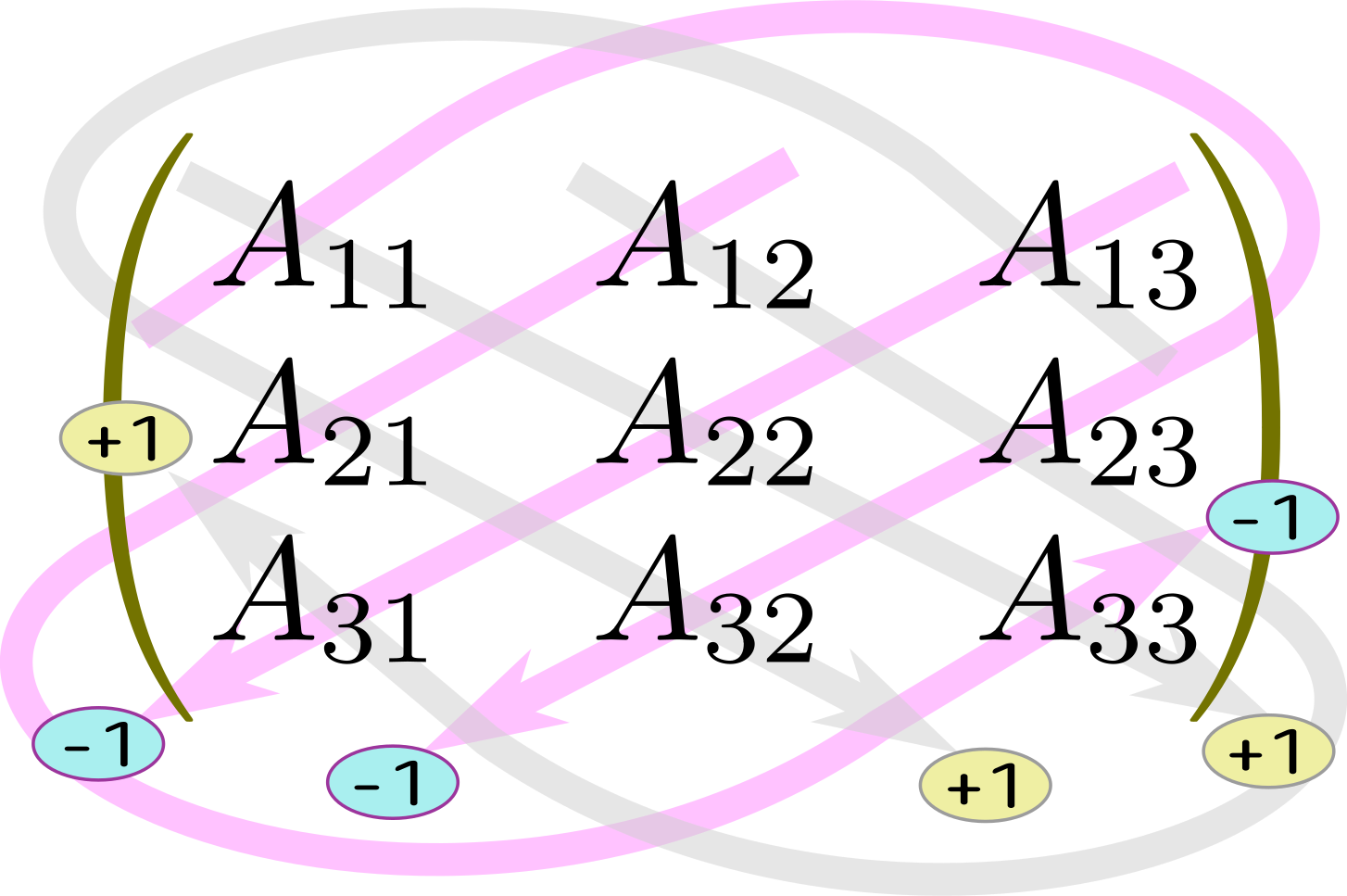
この式が成り立つことを示すには、$\epsilon_{ijk}$が0でないのは$\epsilon_{123},\epsilon_{231},\epsilon_{312}$(以上$+1$)と$\epsilon_{132},\epsilon_{213},\epsilon_{321}$(以上$-1$)の6通りしかなく、

に示したような6種類の項の足し算となる(上の式の左辺でも右辺でも!)ことを確認すればよい。
なお、もう一つ、
\begin{align}
{1\over 3!}\sum_{\dum[xcolor]{i},\dum[ycolor]{j},\dum[zcolor]{k},\dum[rcolor]{\ell},\dum[thetacolor]{m},\dum[phicolor]{n}}
\epsilon_{\dml[xcolor]{i}\dml[ycolor]{j}\dml[zcolor]{k}}
\epsilon_{\dml[rcolor]{\ell}\dml[thetacolor]{m}\dml[phicolor]{n}}
A_{\dmr[xcolor]{i}\dmr[rcolor]{\ell}}A_{\dmr[ycolor]{j}\dmr[thetacolor]{m}}A_{\dmr[zcolor]{k}\dmr[phicolor]{n}}
\end{align}
という書き方もある(これも等しい)。
以上の性質を使うと、行列式の計算を簡単化することができる。地道にやるための公式としては、
\begin{align}
&\det\mtx[ccc]{A_{11}&A_{12}&A_{13}\\A_{21}&A_{22}&A_{23}\\A_{31}&A_{32}&A_{33} }\nonumber\\
=&A_{11}A_{22}A_{33}+A_{12}A_{23}A_{31}+A_{13}A_{21}A_{32}\nonumber\\
&-A_{11}A_{23}A_{32}-A_{12}A_{21}A_{33}-A_{31}A_{22}A_{13}
\end{align}
がある。これを図で表現したのが
である。
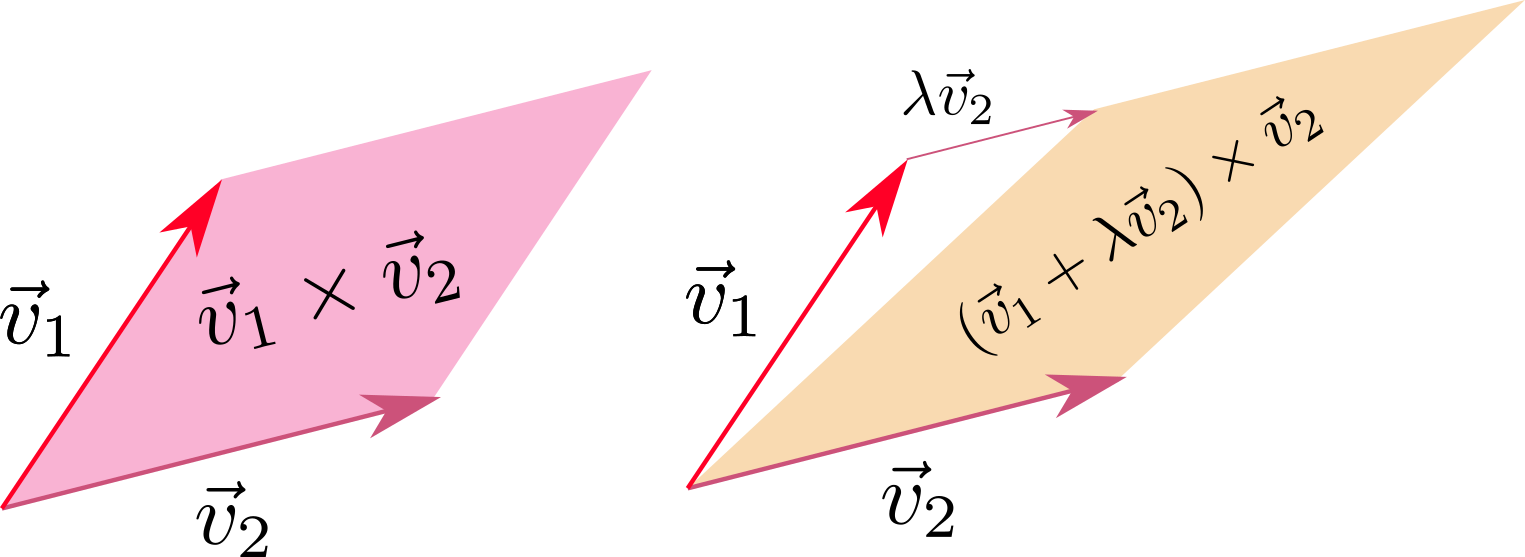
以下の操作をしても行列式が不変であることを使うと、少し計算を省力化できる。
行列式を不変にする変形
- ある(行または列)に別の(行または列)の定数倍を足す。
- ある(行または列)とある(行または列)を交換し、どちらか片方の(行または列)を$-1$倍する(行列式全体の符号を反転してもよい)。
上の一つの文章の中に現れる(行または列)は同じものを選ぶ。
なお、ここでは$3\times3$行列の場合で説明したが、この結果は任意の正方行列で正しい。
上の変形の例を式で書くと、
\begin{align}
\det\mt{A}\kakko{\vec v_1,\vec v_2,\vec v_3}
=& \det\mt{A}\kakko{\vec v_1,\vec v_2+\alpha\vec v_1,\vec v_3}\\
\det\mt{A}\kakko{\vec v_1,\vec v_2,\vec v_3}
=& \det\mt{A}\kakko{\vec v_1,\vec v_3,-\vec v_2}= -\det\mt{A}\kakko{\vec v_1,\vec v_3,\vec v_2}
\end{align}
である。なお、$3\times3$行列の場合、サイクリック置換で不変
\begin{align}
\det\mt{A}\kakko{\vec v_1,\vec v_2,\vec v_3}
=& \det\mt{A}\kakko{\vec v_3,\vec v_1,\vec v_2}
\end{align}
も言える。
2次元では$\det\mt{A}\kakko{\vec v_1,\vec v_2}=-\det\mt{A}\kakko{\vec v_2,\vec v_1}$となるのでサイクリック置換で不変でない。奇数次元か偶数次元かで違う。
簡単な例をやってみよう。
\begin{equation}
\begin{array}{rrll}
(1)&& \mtx[ccc]{1&2&3\\4&5&6\\7&8&9}&\kokode{1行めの-4倍を\atop 2行めに足す}
\nonumber\\
(2)&=& \mtx[ccc]{1&2&3\\0&-3&-6\\7&8&9}&\kokode{1行めの-7倍を\atop 3行めに足す}
\nonumber\\
(3)&=& \mtx[ccc]{1&2&3\\0&-3&-6\\0&-6&-12}&\kokode{1列めの-2倍,-3倍を\atop 2列め、3列めに足す}
\nonumber\\
(4)&=& \mtx[ccc]{1&0&0\\0&-3&-6\\0&-6&-12}&\kokode{2列めの-2倍を\atop 3列めに足す}
\nonumber\\
(5)&=& \mtx[ccc]{1&0&0\\0&-3&0\\0&-6&0}&\kokode{2行めの-2倍を\atop 3行めに足す}
\nonumber\\
(6)&=&\mtx[ccc]{1&0&0\\0&-3&0\\0&0&0}
\end{array}
\end{equation}
となって、この行列の行列式は0となる。なお、0となることは(5)の段階でわかる。あるいは目ざとい人なら、(4)の段階で2行目と3行目が独立でないことに気づいて、行列式が0であることがわかったかもしれない。
3重線形性を使うと、
\begin{align}
&
\det\mtx[c@{~}c@{~}c]{
A_{11}&A_{12}&A_{13}\\
A_{21}&A_{22}&A_{23}\\
A_{31}&A_{32}&A_{33}
}\nonumber\\
=&
\det\mtx[c@{~}c@{~}c]{
A_{11}&0&0\\
A_{21}&A_{22}&A_{23}\\
A_{31}&A_{32}&A_{33}
}
+ \det\mtx[c@{~}c@{~}c]{
0&A_{12}&0\\
A_{21}&A_{22}&A_{23}\\
A_{31}&A_{32}&A_{33}
}
+ \det\mtx[c@{~}c@{~}c]{
0&0&A_{13}\\
A_{21}&A_{22}&A_{23}\\
A_{31}&A_{32}&A_{33}
}\nonumber\\
=&
\det\mtx[c@{~}c@{~}c]{
A_{11}&0&0\\
A_{21}&A_{22}&A_{23}\\
A_{31}&A_{32}&A_{33}
}
\gunderbrace{
- \det\mtx[c@{~}c@{~}c]{
A_{12}&0&0\\
A_{22}&A_{23}&A_{21}\\
A_{32}&A_{33}&A_{31}
}}_{2列めと3列めを入れ替えた}
+ \gunderbrace{
\det\mtx[c@{~}c@{~}c]{
A_{13}&0&0\\
A_{23}&A_{21}&A_{22}\\
A_{33}&A_{31}&A_{32}
}}_{3列めを1列めに持ってきた}\nonumber\\
=&
A_{11}\,
\det\mtx[cc]{
A_{22}&A_{23}\\
A_{32}&A_{33}
}
+A_{12} \left(-
\det\mtx[cc]{
A_{21}&A_{23}\\
A_{31}&A_{33}
}\right)
+A_{13} \,\det\mtx[cc]{
A_{21}&A_{22}\\
A_{31}&A_{32}
}\label{matbunkai}
\end{align}
のような行列式の分解ができる。
上の式の一つめの等号では、1行目の行ベクトルを3本に分解した。
三つめの等号では、
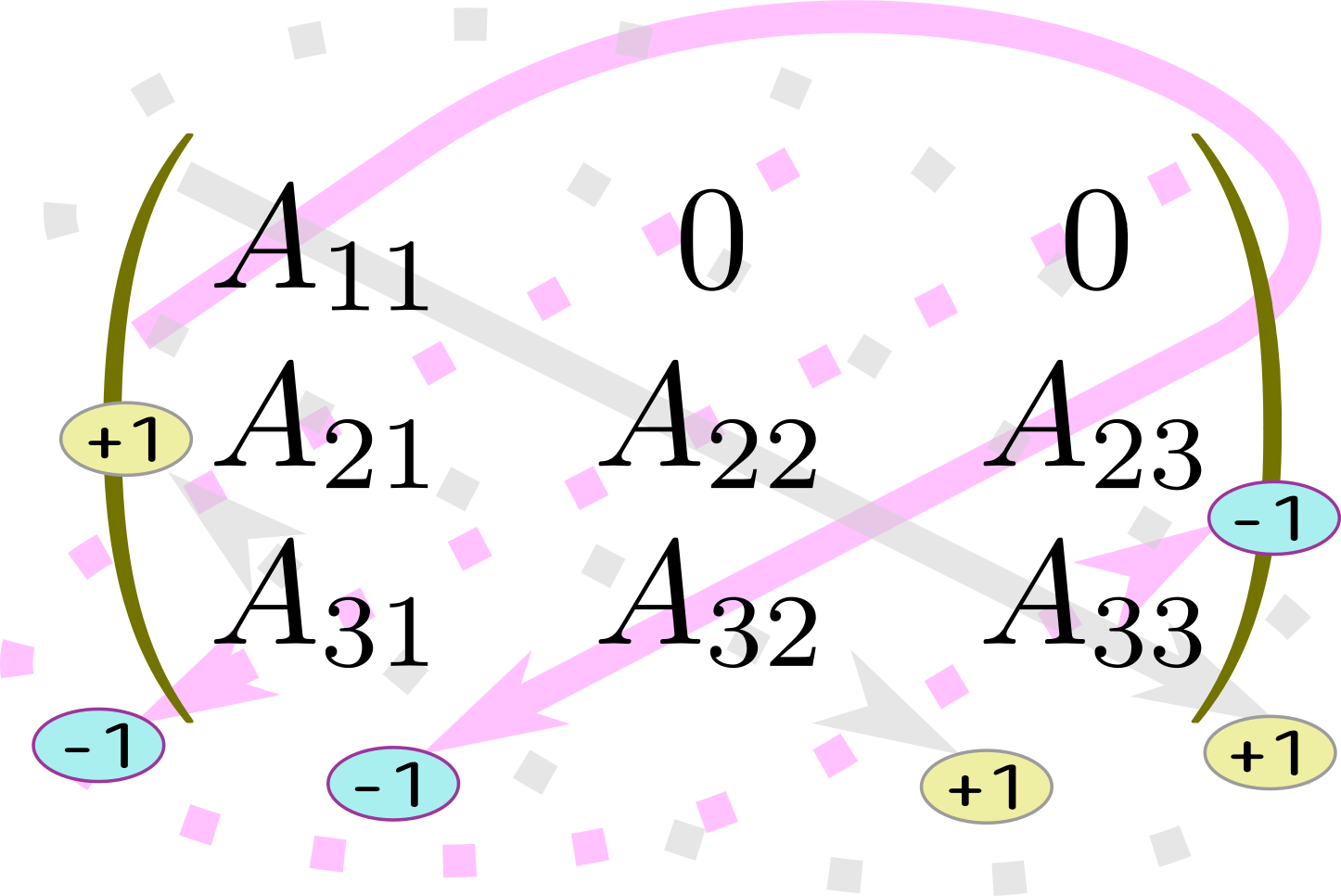
のように行列式の計算を考えれば$2\times2$行列の行列式の計算が出てくることがわかる(図では、0になる積を点線で表現した)のでそれを使った。実線のまま残っている部分の計算がちょうど上の式の第1項の$A_{11}\, \det\mtx[cc]{A_{22}&A_{23}\\A_{32}&A_{33}}$となる(第2項、第3項も同様)。
の最後の式には
\begin{align}
A_{11}\,\gunderbrace{
\det\mtx[cc]{
A_{22}&A_{23}\\
A_{32}&A_{33}
}}_{\tilde A_{11}}
+A_{12} \,\gunderbrace{\left(-
\det\mtx[cc]{
A_{21}&A_{23}\\
A_{31}&A_{33}
}\right)}_{\tilde A_{21}}
+A_{13} \,\gunderbrace{\det\mtx[cc]{
A_{21}&A_{22}\\
A_{31}&A_{32}
}}_{\tilde A_{31}}
\end{align}
のように余因子が現れている。
この式から余因子を定義すると、$A_{ij}$の余因子が計算したければ、行列式から出発して
- $A_{ij}$が(1,1)成分になるように行と列を置換していく(以下は$A_{22}$の場合の例)。置換するごとにマイナス符号が出ることに注意。
$$
\det\mtx[c@{~}c@{~}c]{
A_{11}&A_{12}&A_{13}\\
A_{21}&A_{22}&A_{23}\\
A_{31}&A_{32}&A_{33}
}
=-\det\mtx[c@{~}c@{~}c]{
A_{21}&A_{22}&A_{23}\\
A_{11}&A_{12}&A_{13}\\
A_{31}&A_{32}&A_{33}
}
=\det\mtx[c@{~}c@{~}c]{
A_{22}&A_{21}&A_{23}\\
A_{12}&A_{11}&A_{13}\\
A_{32}&A_{31}&A_{33}
}
$$
- 1行目と1列目を消す。
$$\det\mtx[c@{~}c@{~}c]{
\haiiro{A_{22}}&\haiiro{A_{21}}&\haiiro{A_{23}}\\
\haiiro{A_{12}}&A_{11}&A_{13}\\
\haiiro{A_{32}}&A_{31}&A_{33}
}\to\det\mtx[c@{~}c]{
A_{11}&A_{13}\\
A_{31}&A_{33}
}$$
このようにして、$3\times3$行列の行列式を、$2\times2$行列の行列式(小行列式)に分解して計算することができる。これはさらに次元が高くなって$n\times n$行列になっても同様である。
以上をまとめると、$3\times3$余因子行列の計算は、
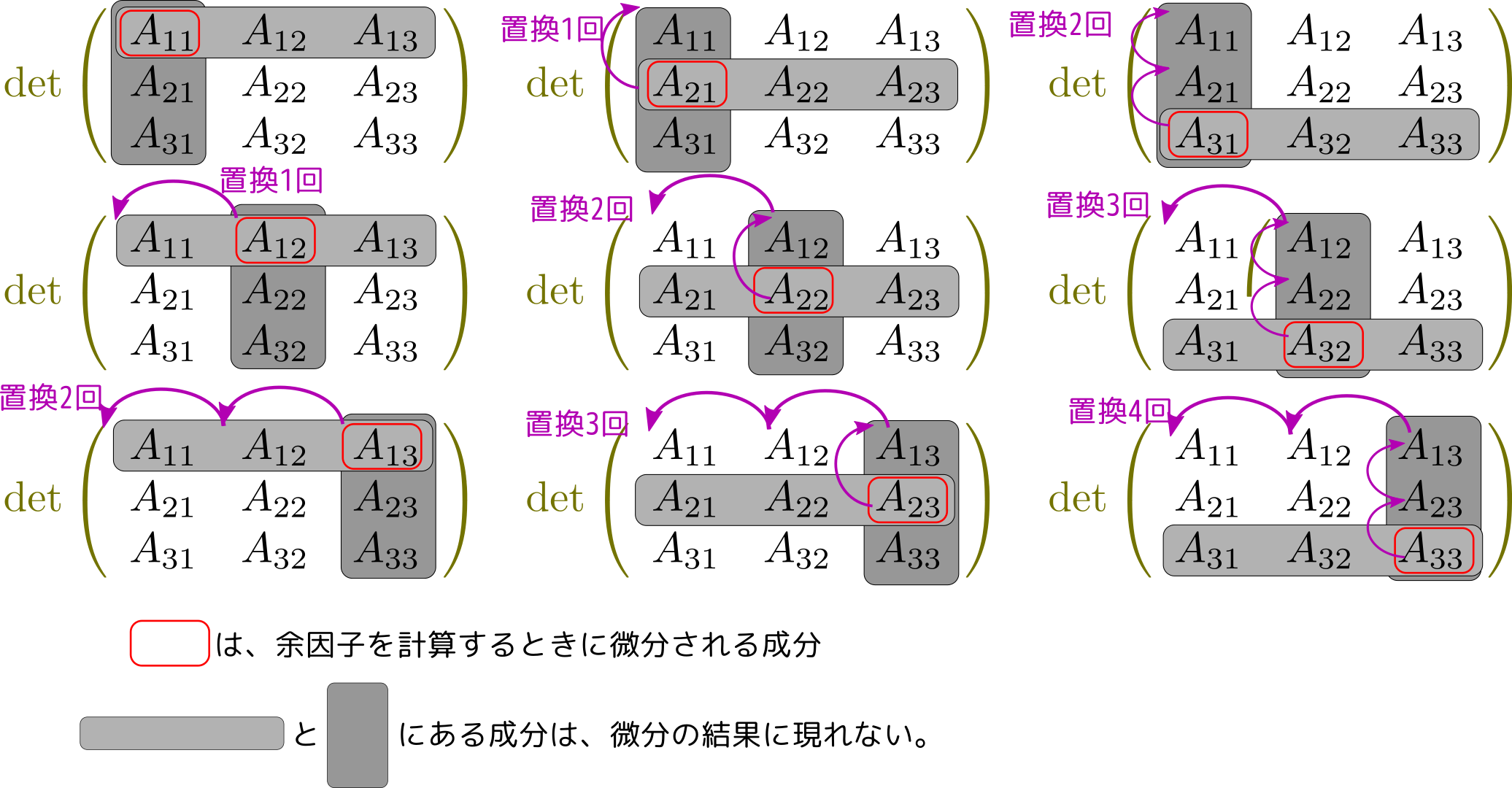
のように図で表現される。
以下のような計算の結果、余因子行列は
\begin{align}
\mtx[ccc]{
\det\mtx{A_{22}&A_{23}\\ A_{32}&A_{33}}
&-\det\mtx{A_{12}&A_{13}\\A_{32}&A_{33}}
&\det\mtx{A_{12}&A_{13}\\ A_{22}&A_{23}}
\\
-\det\mtx{A_{21}&A_{23}\\ A_{31}&A_{33}}
&\det\mtx{A_{11}&A_{13}\\ A_{31}&A_{33}}
&-\det\mtx{A_{11}&A_{13}\\ A_{21}&A_{23}}\\
\det\mtx{A_{21}&A_{22}\\ A_{31}&A_{32}}
&-\det\mtx{A_{11}&A_{12}\\ A_{31}&A_{32}}
&\det\mtx{A_{11}&A_{12}\\ A_{21}&A_{22}}
}
\end{align}
である(微分の前に行と列を置換することによる符号が出ることに注意)。
なお、今日のように式が出てくると、「たくさん覚える式が増えた」と言う人がいるが、授業しているこっちも、皆さんがこんな式をいちいち覚えることを、期待も要請もしていないので安心して欲しい。「どっからこの式出てくるんだっけ?」の部分を把握しておいて、必要になったときに、本なりノートなりから式を引っ張り出してくることができれば充分である。
「全部暗記するぞぉ!」みたいな非効率な勉強をしないように(そんな勉強は後に残りません)。
レポート問題
今日は、レポート問題があります。レポートの提出期限は6/2の水曜日までです(正確には、6/2の23:59まで提出可能です)。解答は
- wordなどのワープロ、TeXなどを使って書いてPDFファイルにする。
- お絵かきソフトなどで書いて画像ファイルにする。
- ノートなどに手書きして写真を撮る。
などの方法で読めるファイルにしてwebClassから提出してください。私が読める形式ならなんでもOKです(読めない場合はメールで連絡します)。マイナーな形式は避けて、PDFか画像にするのが無難です。
問い1
単位行列$\mtx[ccc]{1&0&0\\0&1&0\\0&0&1}$に行列式を変えない変形をしていくことで、行列式が1になる行列をいろいろ作ることができる。以下のような行列を作る過程を示せ(答えはユニークではない場合もあるが、例は一つでいい)。
- $\mtx[ccc]{1&1&1\\0&1&1\\0&0&1}$
- $\mtx[ccc]{0&0&-1\\0&1&0\\1&0&0}$
- $\mtx[ccc]{3&2&1\\2&2&1\\1&1&1}$
問い2
$3\times3$行列を3本の列ベクトル$\vec v_1,\vec v_2,\vec v_3$を並べたものとみなして、行列式を$\det\mt{A}\kakko{\vec v_1,\vec v_2,\vec v_3}$のような、このベクトルの関数と考える。この3本のベクトルが独立でなければ、行列式が0となることを示せ。
ヒント:独立でないということは、ある実数(スカラー)$\alpha,\beta$を使うと、$\vec v_3=\alpha \vec v_1+\beta\vec v_2$となる。
以上で第6回の授業は終わりです。webClassに行って、アンケートに答えてください。レポート提出もよろしく。
物理数学I webclass
この感想・コメントシートに書かれたことについては、代表的なものに対しては次のページで返答します。
なお、webClassに情報を載せていますが、木と金の11:50〜12:50の間、オンラインオフィスアワーとしてzoomを開いてます。質問や相談などがある人は来て話してください。