「物理数学Ⅰ」2021年度講義録第7回

前回の感想・コメントシートから

　前回の授業の「感想・コメント」の欄に書かれたことと、それに対する返答は、

にありますので見ておいてください。

　前回までで、$2\times2$と$3\times3$の行列の行列式と逆行列の作り方をやりました。今回はいっきに「$N\times N$行列の行列式と逆行列」を考えましょう。

　$3\times3$の場合を思い出しておくと、 \begin{align} \det\mt{A}=\sum_{\dum[xcolor]{i},\dum[ycolor]{j},\dum[zcolor]{k}}\epsilon_{\dml[xcolor]{i}\dml[ycolor]{j}\dml[zcolor]{k}}A_{\dmr[xcolor]{i}1}A_{\dmr[ycolor]{j}2}A_{\dmr[zcolor]{k}3} \end{align} がレヴィ・チビタ記号を使った行列式の表現でした（そしてこれを微分すると余因子が計算できて、逆行列を作ることができた）。

　その流れに乗って、まずは$N$次元のレヴィ・チビタ記号を考えます。

　まず任意次元のレヴィ・チビタ記号について確認しておこう。

　上の2.は隣り合う二つの添字に対する式だが、たとえば隣の隣と入れ替えるのであれば、 \begin{equation} \epsilon_{\cdots ijk\cdots} = -\epsilon_{\cdots jik\cdots} = \epsilon_{\cdots jki\cdots} = -\epsilon_{\cdots kji\cdots} \end{equation} となるので、やはり符号は反転する。今入れ替えた$i$と$k$の間に$M$個の添字（$j_1j_2\cdots j_\sM$）があったとしても、 \begin{align} \epsilon_{\cdots ij_1j_2\cdots j_\sM k\cdots} =& (-1)^M\epsilon_{\cdots \gunderbrace{j_1j_2\cdots j_\sM}_{M個} ik\cdots}\nonumber\\ =& -(-1)^M\epsilon_{\cdots j_1j_2\cdots j_\sM ki\cdots} = -\epsilon_{\cdots k\gunderbrace{j_1j_2\cdots j_\sM}_{M個} i\cdots} \end{align} となって、やはり符号は反転する。よって

と表現しても同じことになる。

　ゆえに、レヴィ・チビタ記号は同じ添字が二つ以上あると0になる。

N×N行列の行列式

　以上のようなレヴィ・チビタ記号を使って、

と定義する（これを使って逆行列も後で定義する）。

　たとえば$4\times4$ならば4次元のレヴィ・チビタ記号を$\epsilon_{ijk\ell}$を使って、$\det\mt{A}=\sum_{\dum[xcolor]{i},\dum[ycolor]{j},\dum[zcolor]{k},\dum[thetacolor]{\ell}}\epsilon_{\dum[xcolor]{i}\dum[ycolor]{j}\dum[zcolor]{k}\dum[thetacolor]{\ell}}A_{\dum[xcolor]{i}1}A_{\dum[ycolor]{j}2}A_{\dum[zcolor]{k}3}A_{\dum[thetacolor]{\ell}4}$と行列式が定義されることになる。

　$3\times3$行列の行列式に3重線形性があったように、

が成り立つ（行ベクトルの方についても同様である）。これがあるので

は$N\times N$の場合でも同様に使える。

　上の(1)と(3)は行に対する操作、(2)と(4)は列に対する操作である。

　実は(1)を複数回使うと(3)は実現できる。 \begin{equation} \begin{array}{rll} &\det\kakko{\cdots,\vec v_i,\cdots,\vec v_j,\cdots}&\kokode{i番目にj番目\times(-1)を足す}\\ =&\det\kakko{\cdots,\vec v_i-\vec v_j,\cdots,\vec v_j,\cdots}&\kokode{j番目にi番目を足す}\\ =&\det\kakko{\cdots,\vec v_i-\vec v_j,\cdots,\vec v_i,\cdots}&\kokode{i番目にj番目\times(-1)を足す}\\ =&\det\kakko{\cdots,-\vec v_j,\cdots,\vec v_i,\cdots} \end{array} \end{equation}

　(4)も同様である。

行列式の幾何学的意味

　$2\times2$行列の行列式は「列ベクトル2本の作る平行四辺形の体積」であり、$3\times3$行列の行列式は「列ベクトル3本の作る平行六面体の体積」であった。類推から、$N\times N$行列の行列式は「列ベクトル$N$本の作る$N$次元立体の`体積'」となる。より正確に言うと行列式は「その行列の表す線形写像によってその空間の体積が何倍になるか」を表す量だと言える。2次元の場合で描いたのが下の図である。

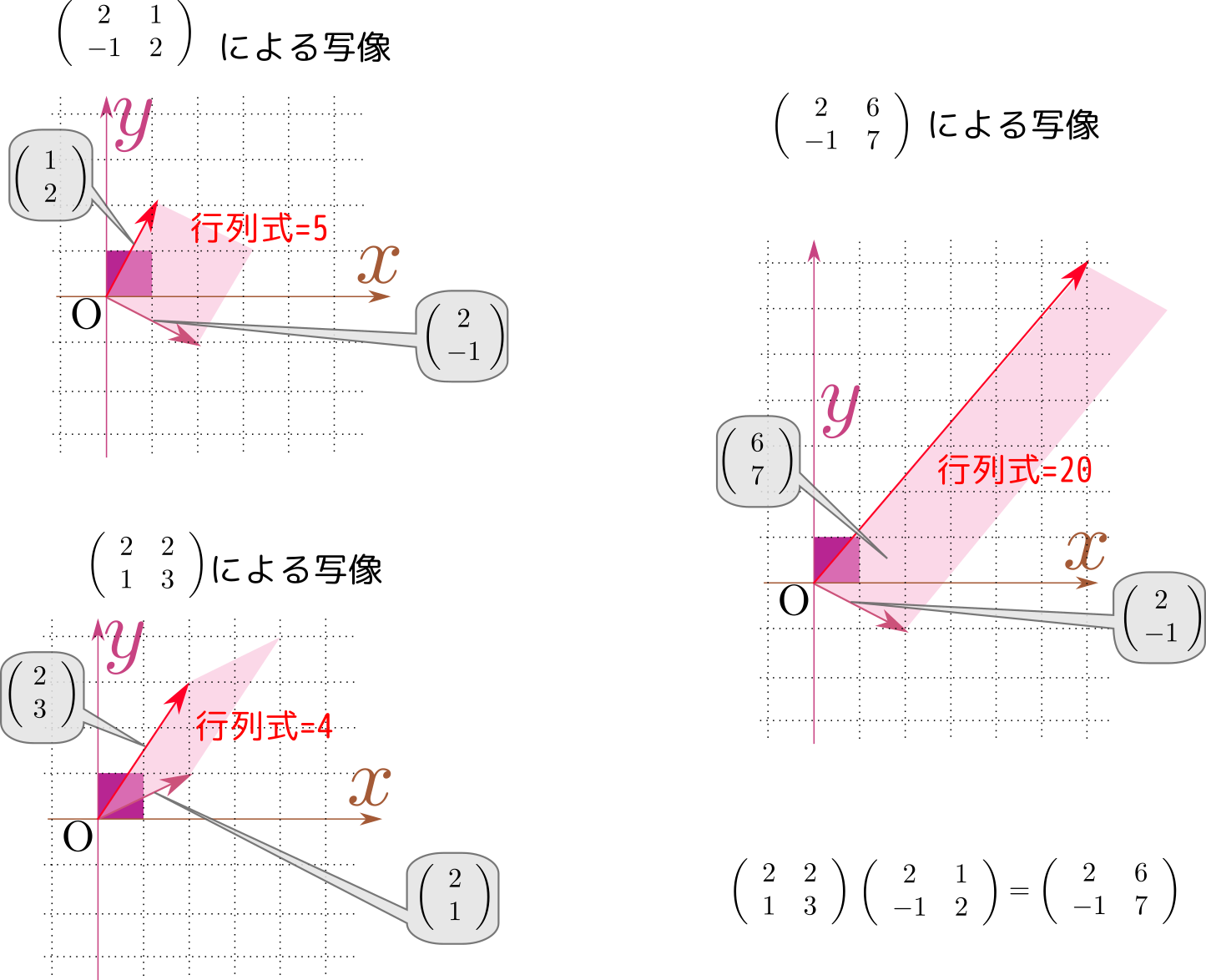
このことから直観的に、以下が成り立つことがわかる。

　これを具体的に行列式の定義に代入して計算して確かめようとすると、少し面倒だが、行列式の$N$重線形性を使うと比較的計算量少なく証明できる。

　まず行列を$\mt{A}$なら$\mtx[c@{\,}c@{\,}c@{\,}c]{\tatevec{\vec A_1}&\tatevec{\vec A_2}&\cdots&\tatevec{\vec A_\sN}}$、$\mt{B}$なら$\mtx[c@{\,}c@{\,}c@{\,}c]{\tatevec{\vec B_1}&\tatevec{\vec B_2}&\cdots&\tatevec{\vec B_\sN}}$のように列ベクトルを並べたものとみなして考えよう。同様に、行列の積は \begin{align} \det\kakko{\mt{AB}}=\det\Kakko{\tatevec{\mt{A}\vec B_1},\tatevec{\mt{A}\vec B_2},\cdots,\tatevec{\mt{A}\vec B_\sN}} \end{align} と表現できる。ここで、$\mt{A}\vec B_k$というベクトルは \begin{align} \mt{A}\vec B_k=\sum_{\dum{i}=1}^N\vec A_{\dml{i}} B_{k\dmr{i}} \end{align} のように$\vec A_*$の線形結合で表現できることを思い出す。

　よって、 \begin{align} \det\kakko{\mt{AB}}= \det\Kakko{ \sum_{\dum{j_1}}\vec A_{\dml{j_1}}B_{1\dmr{j_1}}, \sum_{\dum[ycolor]{j_2}}\vec A_{\dml[ycolor]{j_2}}B_{2\dmr[ycolor]{j_2}}, \cdots, \sum_{\dum[zcolor]{j_\sN}}\vec A_{\dml[zcolor]{j_\sN}}B_{\sN\dmr[zcolor]{j_\sN}}} \end{align} なのだが、$N$重線形性を使えば$\vec A_j$の係数であるところの$B_{ij}$をどんどん外に出していく。結果は \begin{align} \det\kakko{\mt{AB}}= \sum_{\dum{j_1},\dum[ycolor]{j_2},\cdots\dum[zcolor]{j_\sN}=1}^N B_{1\dml{j_1}}B_{2\dml[ycolor]{j_2}}\cdots B_{\sN\dml[zcolor]{j_\sN}}\det\Kakko{\vec A_{\dmr{j_1}},\vec A_{\dmr[ycolor]{j_2}},\cdots,\vec A_{\dmr[zcolor]{j_\sN}}} \end{align} の形になる。ここで、後ろの$\det\Kakko{\vec A_{\dmr{j_1}},\vec A_{\dmr[ycolor]{j_2}},\cdots,\vec A_{\dmr[zcolor]{j_\sN}}}$は$j_1,j_2,\cdots,j_\sN$が$1,2,\cdots,N$の置換でない限り0になる（添字が同じ値になると、行列式の反対称性から0）。

　この置換が偶置換なら結果は$\det\Kakko{\vec A_1,\vec A_2,\cdots,\vec A_\sN}$になり、奇置換なら結果は$-\det\Kakko{\vec A_1,\vec A_2,\cdots,\vec A_\sN}$となるから、 \begin{align} \det\kakko{\mt{AB}}= \gunderbrace{ \sum_{\dum{j_1},\dum[ycolor]{j_2},\cdots\dum[zcolor]{j_\sN}=1}^N B_{1\dml{j_1}}B_{2\dml[ycolor]{j_2}}\cdots B_{\sN\dml[zcolor]{j_\sN}}\epsilon_{\dmr{j_1}\dmr[ycolor]{j_2}\cdots\dmr[zcolor]{j_\sN}}}_{\det\mt{B}} \det\Kakko{\vec A_{1},\vec A_{2},\cdots,\vec A_{\sN}} \end{align} となり、証明された。

　2次元平面を直交座標$(\xcol{x},\ycol{y})$で表したときの微小体積は$\coldx\coldy$だが、極座標$(\rcol{r},\thetacol{\theta})$で表したときの微小体積は$\rcol{r}\coldr\coldtheta$である。これは

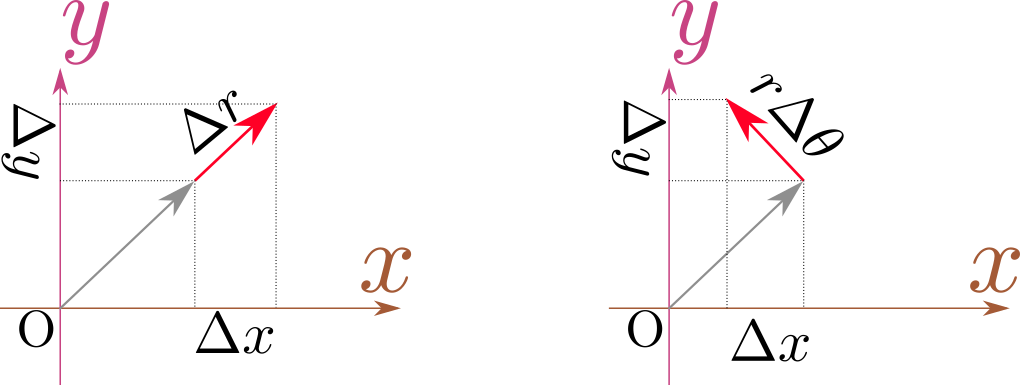
のように図を描いて \begin{align} \Delta x=&\Delta r\cos \theta- \rcol{r}\Delta\theta\sin\theta\\ \Delta y=&\Delta r\sin \theta+ \rcol{r}\Delta\theta\cos\theta \end{align} という関係があること（図は$\Delta r$のみがあるときと$\rcol{r}\Delta\theta$のみがあるときを表現しているが、両方があるときは和になる）を読み取り、さらにそれを行列で \begin{align} \mtx[c]{\Delta x\\ \Delta y}=\mtx{\cos \theta & -\rcol{r}\sin\theta\\ \sin \theta&\rcol{r}\cos \theta}\mtx[c]{\Delta r\\ \Delta \theta} \end{align} と表現した後でこの行列の行列式を考える。すると、面積（2次元体積）の比が、$\rcol{r}$であることがわかる。

余因子

　$3\times3$のときと同様に、$A_{qp}$の余因子$\tilde A_{pq}$を \begin{equation} \tilde A_{pq}=\PD{}{\kuro{A_{qp}}}\left( \sum_{\dum[xcolor]{i},\dum[ycolor]{j},{\dum[zcolor]{k}},\cdots,\dum[tcolor]{\ell}}\epsilon_{\dml[xcolor]{i}\dml[ycolor]{j}\dml[zcolor]{k}\cdots\dml[tcolor]{\ell}}A_{\dmr[xcolor]{i}1}A_{\dmr[ycolor]{j}2}A_{\dmr[zcolor]{k}3}\cdots A_{\dmr[tcolor]{\ell}\sN}\right)=\PD{\left(\det~\mt{A}\right)}{\kuro{A_{qp}}} \end{equation} で定義しよう。

　$N\times N$の場合も、$\tilde A_{qp}$を並べた行列のことを余因子行列と呼ぶ。

　微分を使って表現しているが、難しい計算をしているわけではなく、行列式は$A_{qp}$の1次式でしかないので、やっている計算は係数を求めているだけである。 \begin{equation} \sum_{\dum[xcolor]{i}}\tilde A_{p\dml[xcolor]{i}}A_{\dmr[xcolor]{i}q}=0~~~~~~(p\neq qのとき)\label{tildeAjouken} \end{equation} が成り立つことはすぐにわかる。まず$p=1$にして代入してみると、 \begin{align} \sum_{\dum{i}} \tilde A_{1\dml{i}}A_{\dmr{i}q}=\sum_{\dum{i},\dum[ycolor]{j},\dum[zcolor]{k},\cdots,\tcol{\ell}}\epsilon_{\dml{i}\dml[ycolor]{j}\dml[zcolor]{k}\cdots\dml[tcolor]{\ell}}A_{\dmr{i}q}A_{\dmr[ycolor]{j}2}A_{\dmr[zcolor]{k}3}\cdots A_{\dmr[tcolor]{\ell}\sN} \end{align} であるが、$q$が1でないなら、$2,3,\cdots,N$のどれかである。たとえば$q=2$なら \begin{align} \sum_{\dum{i}} \tilde A_{1\dml{i}}A_{\dmr{i}2}=\sum_{\dum{i},\dum[ycolor]{j},\dum[zcolor]{k},\cdots,\tcol{\ell}}\epsilon_{\dml{i}\dml[ycolor]{j}\dml[zcolor]{k}\cdots\dml[tcolor]{\ell}} \gunderbrace{A_{\dmr{i}2}A_{\dmr[ycolor]{j}2}}_{\dum{i}\leftrightarrow\dum[ycolor]{j}で対称}A_{\dmr[zcolor]{k}3}\cdots A_{\dmr[tcolor]{\ell}\sN} \end{align} となるが、レヴィ・チビタ記号は$\dum{i}\leftrightarrow\dum[ycolor]{j}$で反対称だから、この和は0になる。

　$K_{ij}$が$i,j$の交換で反対称、$L_{ij}$が$i,j$の交換で対称であれば、$\sum_{\dum{i},\dum[ycolor]{j}}K_{\dml{i}\dml[ycolor]{j}}L_{\dmr{i}\dmr[ycolor]{j}}=0$になる。足し算の過程で（$m\ne n$として）$K_{mn}L_{mn}$と$K_{nm}L_{nm}$が一回ずつ現れ、その和が0になる。$m=n$のときは$K_{nm}=0$である。

　$q$が$3,4,5,\cdots$などの場合も同様である。

　こうして、

がわかった。

　では$q=1$ではどうなるかというと、 \begin{equation} \sum_{\dum[xcolor]{i},\dum[ycolor]{j},\dum[zcolor]{k},\cdots,\tcol{\ell}}\epsilon_{\dml[xcolor]{i}\dml[ycolor]{j}\dml[zcolor]{k}\cdots\dml[tcolor]{\ell}}A_{\dmr[xcolor]{i}1}A_{\dmr[ycolor]{j}2}A_{\dmr[zcolor]{k}3}\cdots A_{\dmr[tcolor]{\ell}\sN} \end{equation} となる。これはついさっき定義した（$N\times N$行列の）行列式$\det~\mt{A}$そのものである。

　微分を使った表現を使うと \begin{align} \sum_{\dum{i}} \tilde A_{1\dml{i}}A_{\dmr{i}1} = \sum_{\dum{i}} {\partial\left(\det\mt{A}\right)\over \partial A_{\dml{i}1}}A_{\dmr{i}1} \end{align} という式が出る。これは（以下にしめすように）行列式の$N$重線形性からすぐにわかる。

　1列めだけではなく任意の列に対してこれが成り立つことを示そう。まず、元の$\mt{A}$のうち、$q$列めの成分だけを$\lambda$倍した行列 \begin{align} \mtx[cccccc]{ A_{11}&A_{12}&\cdots&\lambda A_{1q}&\cdots&A_{1\sN}\\ A_{21}&A_{22}&\cdots&\lambda A_{2q}&\cdots&A_{2\sN}\\ \vdots&\vdots &&\vdots & &\vdots\\ A_{\sN1}&A_{\sN2}&\cdots&\lambda A_{\sN q}&\cdots&A_{\sN\sN} } \end{align} を考える。この行列を$\mt{L}$としよう。$\mt{L}$の行列式は、もとの行列の$\lambda$倍である。すなわち \begin{align} \det\mt{L}=\det \mtx[cccccc]{ A_{11}&A_{12}&\cdots&\lambda A_{1q}&\cdots&A_{1\sN}\\ A_{21}&A_{22}&\cdots&\lambda A_{2q}&\cdots&A_{2\sN}\\ \vdots&\vdots & &\vdots & &\vdots\\ A_{\sN1}&A_{\sN2}&\cdots&\lambda A_{\sN q}&\cdots&A_{\sN\sN} } =\lambda \det \mt{A} \end{align} なのだが、この式の両辺を$\lambda$で微分すると（$\lambda$を含むのは$q$列めだけであることに注意）、 \begin{align} \sum_{\dum{i}=1}^N \gunderbrace{{\partial \det\mt{L}\over \partial L_{\dml{i}q}}}_{\tilde L_{q\dml{i}}}\gunderbrace{\partial L_{\dmr{i}q}\over \partial \lambda}_{A_{\dmr{i}q}}=\det \mt{A} \end{align} という式が出る。ここで、$\tilde L_{qi}$にはすでに$\lambda$は含まれていないので、$\tilde A_{qi}$に等しく、 \begin{align} \sum_{\dum{i}=1}^N\tilde A_{q\dml{i}}A_{\dmr{i}q}=\det\mt{A} \end{align} が示せた。

　これで、 \begin{equation} \sum_{\dum[xcolor]{q}} \tilde A_{p\dml[xcolor]{q}}A_{\dmr[xcolor]{q}r}= \begin{cases} \det~\mt{A}&(p=r)\\ 0& (p\neq r) \end{cases}\label{tildeAA} \end{equation} がわかった。よって、逆行列は \begin{equation} \mt{A^{-1}}={1\over \det\mt{A}}\mt{\tilde A} \end{equation} で定義されることになる。

連立方程式を行列で解く

　行列は線形の連立方程式を解くのに使える、ということを導入としていたので、ここで具体的に「方程式を解く」という作業を行列を使ってやってみよう。$\xcol{\vec x}$が変数、$\vec A$を定数としてこの二つの関係が行列$\mt{M}$を使って \begin{align} \mt{M}\xcol{\vec x}=\vec A\label{Mx} \end{align} と表現されているとする。逆行列$\mt{A^{-1}}$が存在しているならば、 \begin{align} \xcol{\vec x}=\mt{M^{-1}}\vec A \end{align} で$\xcol{\vec x}$が求められる。

　よって具体的な計算の上で問題となるのは

• 逆行列をいかにして計算するか？
• 逆行列がない場合はどうするか？
• 逆行列がユニークに決まらない場合はどうするか？

ということである。この問題を考えていく上で、「どういう場合に逆行列がなかったりユニークでなくなったりするのかを知る」ということも目標になる。

　行列式が0のときは、$\mt{M^{-1}}$が存在しないので、$\xcol{\vec x}=\mt{M^{-1}}\vec A$で$\xcol{\vec x}$を求めるというわけにはいかない。ではまったく$\xcol{\vec x}$に関して何の情報も得られないのかというと、そんなことはない。どの程度の情報が得られるのかを以下で考察していこう。

　行列式が0になるのは

• 行列を構成する行ベクトルが独立でない場合
• 行列を構成する列ベクトルが独立でない場合

の二つが考えられる（実はこの二つは同じことである）。

　そのことを示そう。

　前にやった「行列式を不変にする変形」のうち、行に関する操作である

を使うと、行列をかならず「上三角行列」にできることが以下のようにして示せる。

　上三角行列のありがたい性質は、行列式が$A_{11}A_{22}A_{33}\cdots A_{NN}$になることである（それ以外の項は全部0になる）。よって、$A_{ii}$の全てが0でないとき、行列式は0ではない（一つでも0だと、行列式は0になる）。

　$A_{ii}$の全てが0でないとき、上三角行列の行ベクトルは線形独立である。たとえば$\mtx[cccc]{A_{11}&A_{12}&\cdots&A_{NN}}$という列ベクトルは、それより下にあるベクトルをいかに足し算しても作ることはできない（他のベクトルには第1成分が全部0だから！）

　逆に言えば$A_{ii}$が0である場合は、それより下のベクトルを足し算すれば$\mtx[cccccc]{0&0&\cdots&A_{ii}&A_{i(i+1)},\cdots}$というベクトルは必ず作ることができる。

　このとき、行列を行ベクトルを並べたものとみたときの行ベクトルは線形独立ではないということになる。ところで上で行った操作は、まさに行ベクトルの線形結合を取るという操作だったので、線形結合を取ったら独立じゃなかった、ということは「元々独立じゃなかった」ということになる。

　さて、行列式を不変にする変形には、

もあった。こっちを使うと行列を「下三角行列」に直すことができて、同様に行列式が0なら線形独立ではないことが示せる。

　つまり、行列式が0でないときは、行ベクトルは線形独立ではないし、列ベクトルも線形独立ではないのだ。

　列ベクトルが独立でない場合、すなわち、 \begin{align} \mt{M}=\mtx[c@{\,}c@{\,}c@{\,}c]{\nagatatevec{\vec M_1}&\nagatatevec{\vec M_2}&\cdots&\nagatatevec{\vec M_N}} \end{align} としたときに、 \begin{align} \sum_{\dum{i}=1}^N \alpha_{\dml{i}} \vec M_{\dmr{i}}=0 \end{align} なる関係がある場合を考えよう。この式は、行列を使うと \begin{align} \mt{M}\gunderbrace{\mtx[c]{\alpha_1\\\alpha_2\\ \vdots\\\alpha_N}}_{\vec \alpha}=0 \end{align} と書くことができる。これの意味するところは、「$\xcol{\vec x}=\vec X$が方程式$ \mt{M}\xcol{\vec x}=\vec A$の一つの解なら、$\xcol{\vec x}=\vec X+\vec \alpha$も解になる」ということだ。これは「解がユニークに決まらない」と言う状況である。

　さて、ここで行列を形成する列ベクトル$N$本のうち何本が独立なのか、という数を考えよう。この数を「階数(rank)」と呼ぶ。行列は階数が大きいほど多い情報を含んでいる。階数をどのように評価していくか、そしてどのように連立方程式を解いていくか、いう話は次回やろう。

　なお、webClassに情報を載せていますが、木と金の11:50〜12:50の間、オンラインオフィスアワーとしてzoomを開いてます。質問や相談などがある人は来て話してください。

受講者の感想・コメント

　webclassでのアンケートによる、感想・コメントなどをここに記します。

　青字は受講者からの声、赤字は前野よりの返答です。

　主なもの、代表的なもののみについて記し、回答しています。