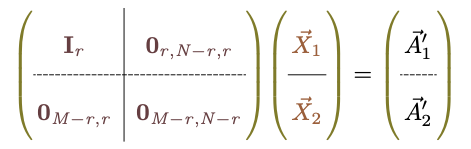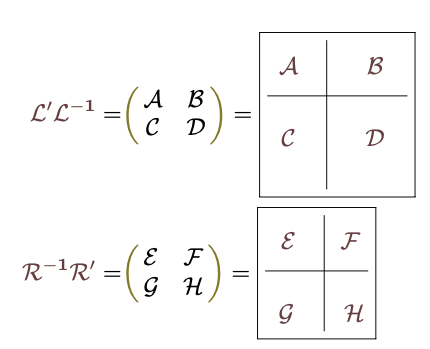以下の話の説明ビデオは↓
基本変形
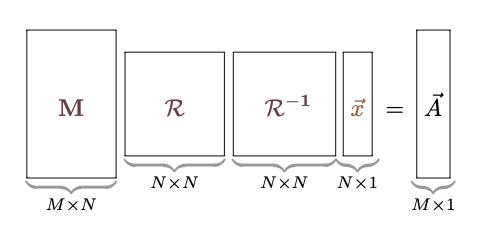
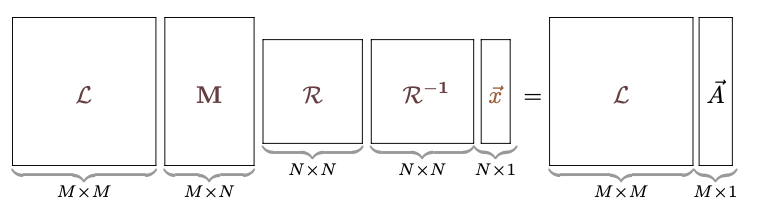
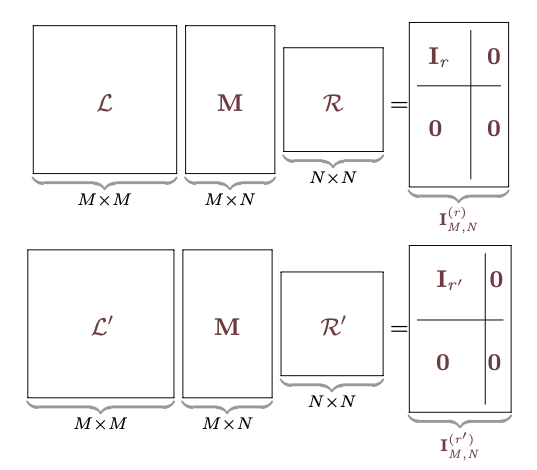
前項で考えた$\mt{\cal L}$と$\mt{\cal R}$は、どちらも逆行列が存在する(行列式が0ではない)行列ではなくてはいけない。
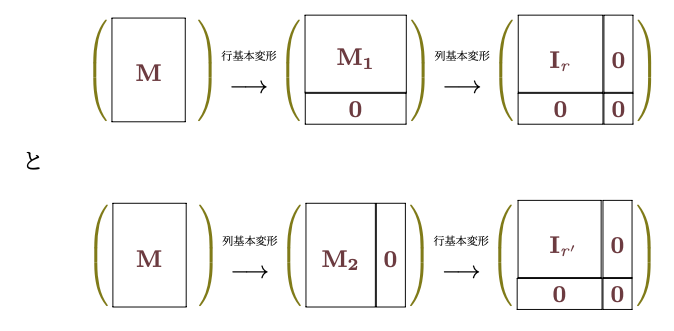
我々の目標である「簡単な行列による表現」を得るためには、以下で示すような「基本変形」の組合せで$\mt{\cal L},\mt{\cal R}$を表せば十分である。操作をいくつかの「単位」に分解することで計算を段階分けして行っていくことができる。
$\mt{\cal L}$で表現された変形の方は、以下の基本変形の組合せで表現する。
行基本変形
- (1)ある行に別の行の定数倍を足す。
- (2)ある行と別の行を交換する。
- (3)ある行を定数倍する(0倍を除く)。
「行基本変形」は「左基本変形」と呼ぶ場合もある。行基本変形は、方程式を定数倍したり線形結合を取ったりしているだけなので、「方程式の持つ情報を不変にする変形」だと考えればよい。
$\mt{\cal R}$による変形は、以下の基本変形の組合せで表現できる。
列基本変形
- ある列に別の列の定数倍を足す。
- ある列と別の列を交換する。
- ある列を定数倍する(0倍を除く)。
「列基本変形」は「右基本変形」と呼ぶ場合もある。列基本変形は、「変数を変更する変形」である。
これらが前にやった「行列式を不変にする変形」に似ていることは気づいただろう((1)の組合せで(2)が実現するのも同じである)。ただし、上の操作の(2)と(3)は行列式は変える操作であることに注意。列基本変形と行基本変形は、行列式を変えてもよい分だけ、「行列式を不変にする変形」よりも範囲が広い。
基本変形の行列による表現
基本変形を行列で表現しておく。さいわい、行基本変形と列基本変形は同じ行列で表現可能である。
まず、$\mt{T_{i\to j}}\kakko{\lambda}$という行列を
\begin{align}
\mt{T_{i\to j}}\kakko{\lambda}\equiv
\mt{I}+\gunderbrace{
\mtx[c|ccc]{
&&{\scriptstyle j列}&\\
\hline
&&\vdots&\\
{\scriptstyle i行}&\cdots&\lambda&\\
&&\\5
}}_{i行j列成分以外は0}
\end{align}
と定義しよう。
これを右から掛けると
\begin{align}
&\mtx[c@{\,}c@{\,}c@{\,}c@{\,}c@{\,}c@{\,}c]{\nagatatevec{\vec v_1}&\cdots&\nagatatevec{\vec v_i}&\cdots&\nagatatevec{\vec v_j}&\cdots&\nagatatevec{\vec v_N}}
\left(
\mt{I}+\gunderbrace{
\mtx[c|ccc]{
&&{\scriptstyle j列}&\\
\hline
&&\vdots&\\
{\scriptstyle i行}&\cdots&\lambda&\\
&&\\
}}_{i行j列成分以外は0}5
\right)\nonumber\\
=&\mtx[c@{\,}c@{\,}c@{\,}c@{\,}c@{\,}c@{\,}c]{\nagatatevec{\vec v_1}&\cdots&\nagatatevec{\vec v_i}&\cdots&\nagatatevec{\vec v_j+\lambda \vec v_i}&\cdots&\nagatatevec{\vec v_N}}
\end{align}
となる。つまり$\mt{T_{i\to j}}\kakko{\lambda}$は「右から掛けると、$j$列めに$i$列めの$\lambda$倍を足すという作用をする」行列である(上の式は$i\lt j$の場合だが、$j\lt i$でも同様)。
左から掛けると
\begin{align}
&
\left(
\mt{I}+\gunderbrace{
\mtx[c|ccc]{
&&{\scriptstyle j列}&\\
\hline
&&\vdots&\\
{\scriptstyle i行}&\cdots&\lambda&\\
&&\\
}}_{i行j列成分以外は0}
\right)
\mtx[c]{\yokovec{\vec w_1}\\\vdots\\\yokovec{\vec w_i}\\\vdots\\\yokovec{\vec w_j}\\\vdots\\\yokovec{\vec w_\sM}}
=\mtx[c]{\yokovec{~~~~\vec w_1~~~~}\\\vdots\\\yokovec{\vec w_i+\lambda\vec w_j}\\\vdots\\\yokovec{~~~~\vec w_j~~~~}\\\vdots\\\yokovec{~~~~\vec w_\sM~~~~}}
\end{align}
$\mt{T_{i\to j}}\kakko{\lambda}$は「左から掛けると、$i$行めに$j$行めの$\lambda$倍を足すという作用をする」行列である(上の式は$i\lt j$の場合だが、$j\lt i$でも同様)。
「ピンと来ない」という人は$3\times3$あたりで実例を作ってみよう(自分で手で計算して納得することは重要!)。
$\mt{T_{1\to 3}}\kakko{\lambda}=\mtx[ccc]{1&0&\lambda\\0&1&0\\0&0&1}$は、右から掛けると3列めに1列めの$\lambda$倍を足す行列であるとともに、左から掛けると1行めに3行めの$\lambda$倍を足す行列である。
\begin{align}
\mtx[c@{\,}c@{\,}c]{A_{11}&A_{12}&A_{13}\\A_{21}&A_{22}&A_{23}\\A_{31}&A_{32}&A_{33}}\mtx[ccc]{1&0&\lambda\\0&1&0\\0&0&1}=&\mtx[ccc]{A_{11}&A_{12}&A_{13}+\lambda A_{11}\\ A_{21} &A_{22}&A_{23}+\lambda A_{21}\\A_{31}&A_{32}&A_{33}+\lambda A_{31}}
\\
\mtx[ccc]{1&0&\lambda\\0&1&0\\0&0&1} \mtx[c@{\,}c@{\,}c]{A_{11}&A_{12}&A_{13}\\A_{21}&A_{22}&A_{23}\\A_{31}&A_{32}&A_{33}}=&\mtx[c@{\,}c@{\,}c]{A_{11}+\!\lambda A_{31}&A_{12}+\!\lambda A_{32}&A_{13}+\!\lambda A_{33}\\ A_{21} &A_{22}&A_{23}\\A_{31}&A_{32}&A_{33}}
\end{align}
と計算してみると、確かにそうなっている。
容易に確認できるが、$\mt{T_{i\to j}}\kakko{\lambda}$には逆行列がある($\mt{T_{i\to j}}\kakko{-\lambda}$である)。
これもピンと来ないという人は、$\mtx[ccc]{1&0&\lambda\\0&1&0\\0&0&1}\mtx[ccc]{1&0&-\lambda\\0&1&0\\0&0&1}$を計算しよう。
次に、以下の行列が「行または列を交換する」操作を表現する行列である。
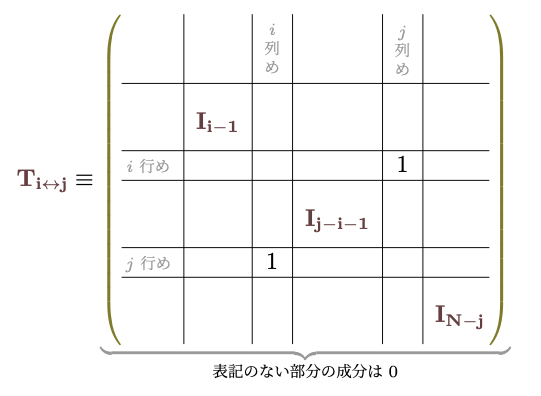
$3\times3$の実例は、$\mt{T_{1\leftrightarrow 2}}=\mtx[ccc]{0&1&0\\1&0&0\\0&0&1}$で、
\begin{align}
\mtx[ccc]{0&1&0\\1&0&0\\0&0&1} \mtx[c@{\,}c@{\,}c]{A_{11}&A_{12}&A_{13}\\A_{21}&A_{22}&A_{23}\\A_{31}&A_{32}&A_{33}}=\mtx[c@{\,}c@{\,}c]{A_{21}&A_{22}&A_{23}\\A_{11}&A_{12}&A_{13}\\A_{32}&A_{31}&A_{33}}
\\
\mtx[c@{\,}c@{\,}c]{A_{11}&A_{12}&A_{13}\\A_{21}&A_{22}&A_{23}\\A_{31}&A_{32}&A_{33}} \mtx[ccc]{0&1&0\\1&0&0\\0&0&1}
=\mtx[c@{\,}c@{\,}c]{A_{12}&A_{11}&A_{13}\\A_{22}&A_{21}&A_{23}\\A_{32}&A_{31}&A_{33}}
\end{align}
となって、左から掛けると行を入れ替え、右から掛けると列を入れ替える。
$\mt{T_{i\leftrightarrow j}}$の逆行列は自分自身である。
最後に、「行または列を定数倍する」を表現するのが以下の行列である。
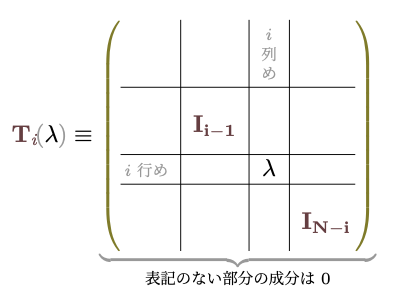
$3\times3$の実例は、$\mt{T}_{3}\kakko{\lambda}=\mtx[ccc]{1&0&0\\0&1&0\\0&0&\lambda}$で、
\begin{align}
\mtx[ccc]{1&0&0\\0&1&0\\0&0&\lambda} \mtx[c@{\,}c@{\,}c]{A_{11}&A_{12}&A_{13}\\A_{21}&A_{22}&A_{23}\\A_{31}&A_{32}&A_{33}}=\mtx[c@{\,}c@{\,}c]{A_{11}&A_{22}&A_{33}\\A_{21}&A_{22}&A_{23}\\\lambda A_{31}&\lambda A_{32}&\lambda A_{33}}
\\
\mtx[c@{\,}c@{\,}c]{A_{11}&A_{12}&A_{13}\\A_{21}&A_{22}&A_{23}\\A_{31}&A_{32}&A_{33}} \mtx[ccc]{1&0&0\\0&1&0\\0&0&\lambda}
=\mtx[c@{\,}c@{\,}c]{A_{11}&A_{12}&\lambda A_{13}\\A_{21}&A_{22}&\lambda A_{33}\\A_{32}&A_{31}&\lambda A_{33}}
\end{align}
となって、左から掛けると行を定数倍し、右から掛けると列を定数倍する。
$\mt{T_{\it i}}\kakko{\lambda}$の逆行列は$\mt{T_{\it i}}\kakko{1\over \lambda}$である。
(4)も同様である。
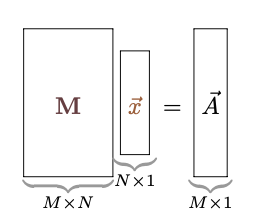
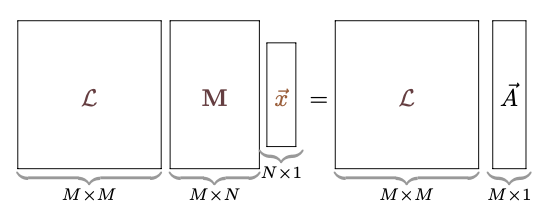
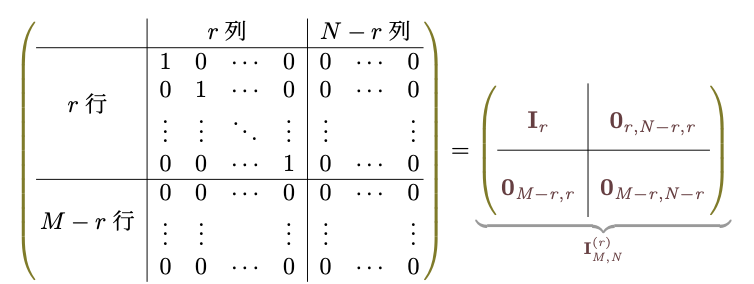
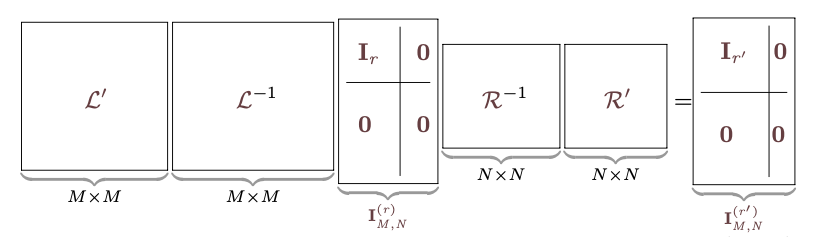
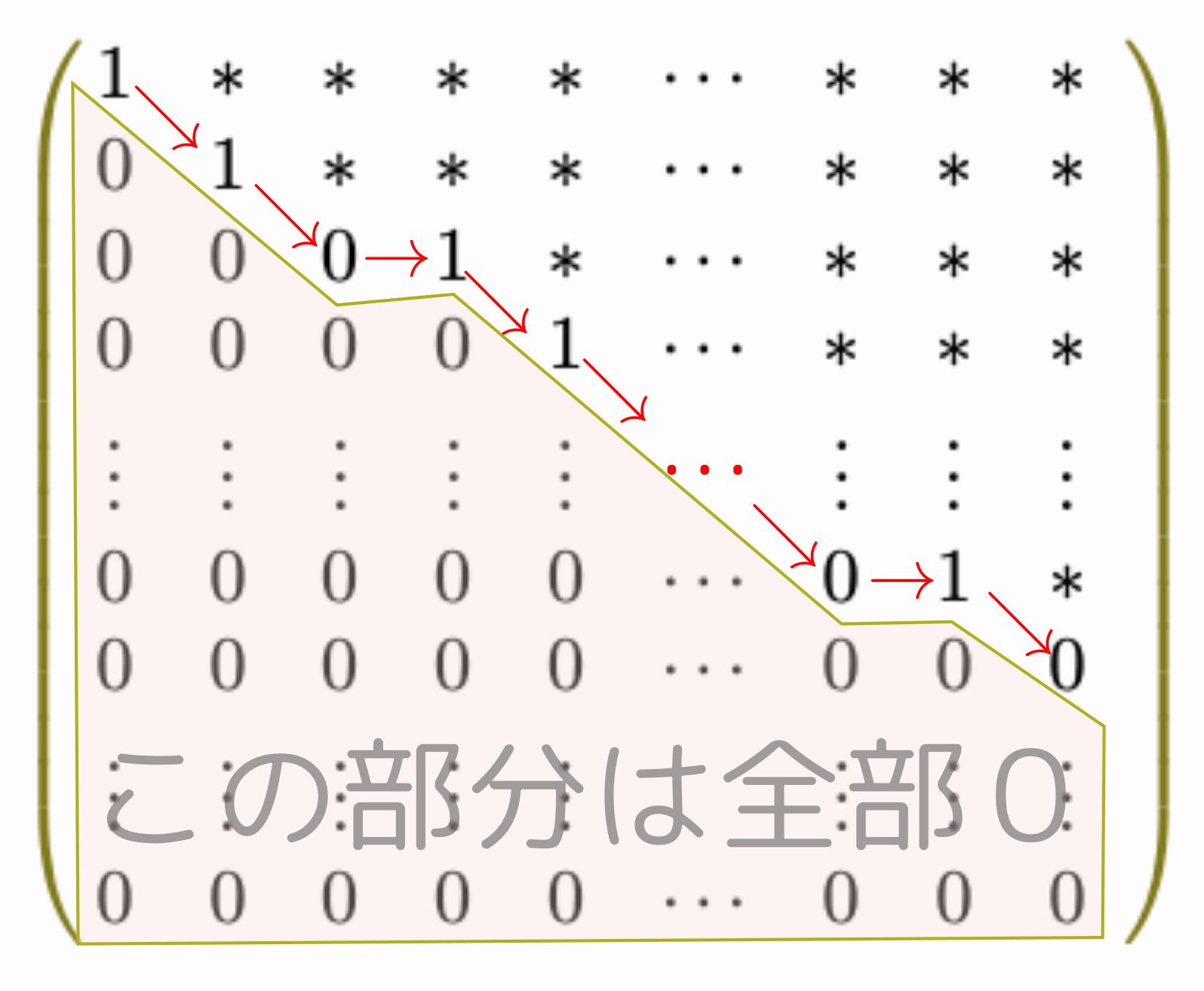
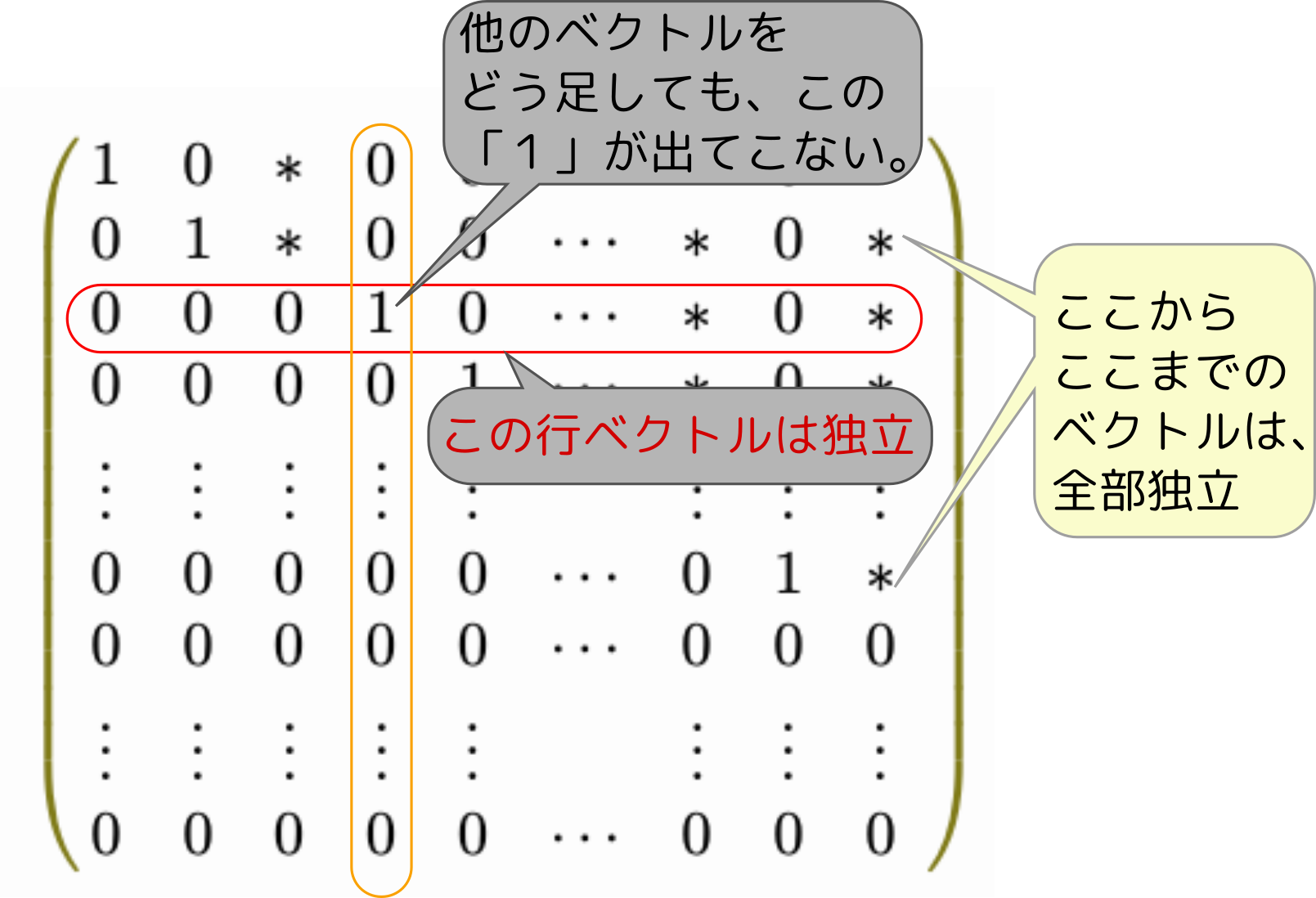
 を元の、
を元の、 に戻すことができる条件である。戻せないとしたら、それは式が持っていた情報を失ってしまったことになる。
に戻すことができる条件である。戻せないとしたら、それは式が持っていた情報を失ってしまったことになる。