「物理数学Ⅰ」2021年度講義録第9回

前回の感想・コメントシートから

　前回の授業の「感想・コメント」の欄に書かれたことと、それに対する返答は、

にありますので見ておいてください。

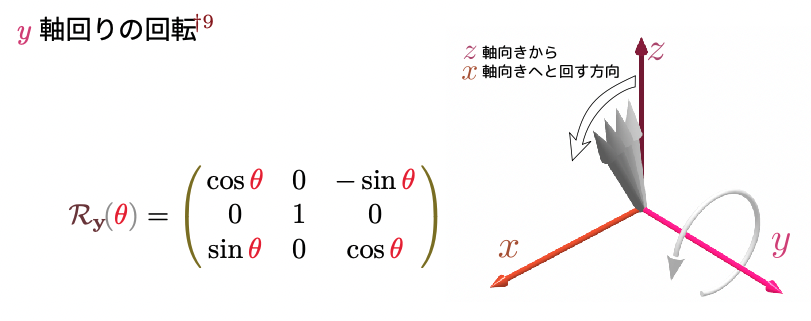
　前回までで行列式・逆行列を使って連立方程式を解く話をしました。少し物理よりに話をシフトして、今日は「回転」を行列で表す話をしましょう。

2次元平面でのベクトルの回転

図形で考えるベクトルの回転

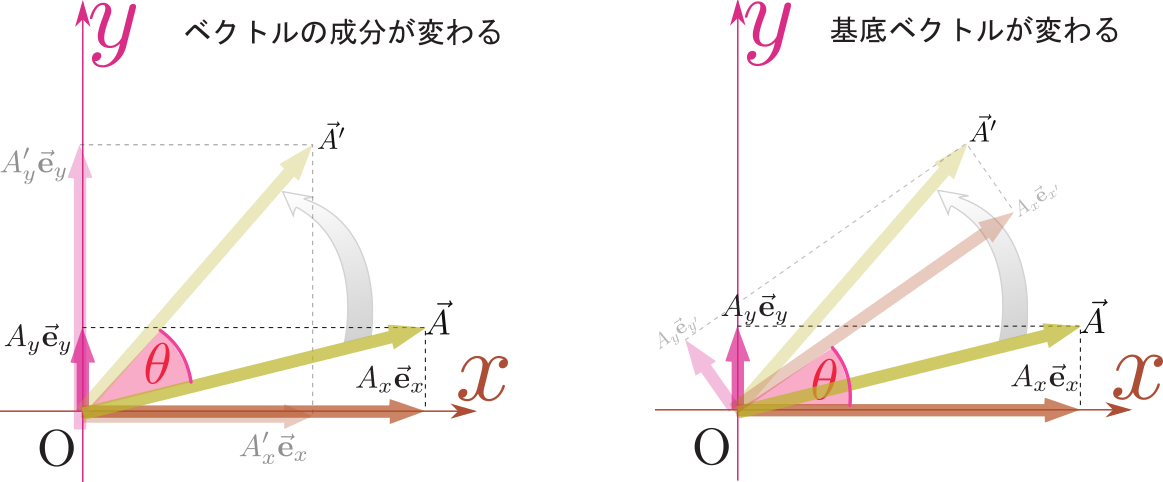
　ここでは、2次元平面の上でベクトル$\vec A$を角度$\thetacol{\theta}$だけ回転させたベクトル$\vec A'$をどのように作れば（あるいは数式上で表現すれば）よいかということを考えよう。図で描くならば

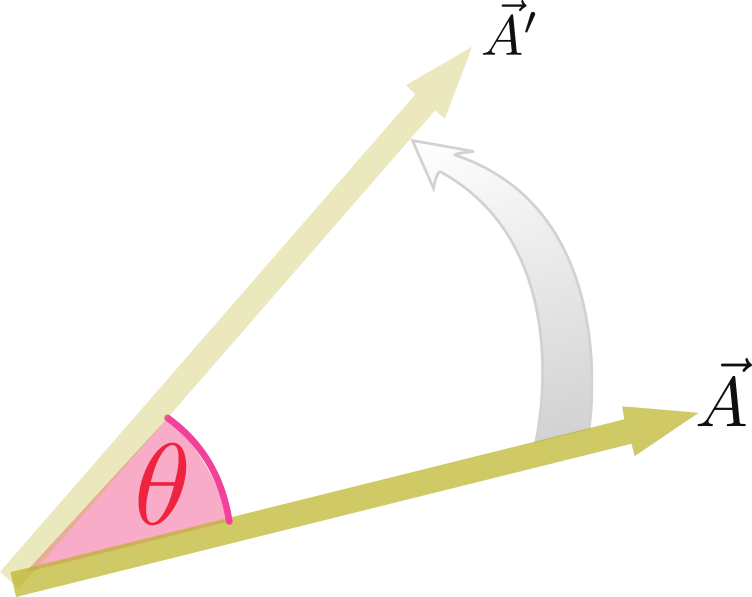
のような状況である。

　最初に一つ確認しておくが、この回転の操作を$R\kakko{\vec A}$のように表したとき、この$R\kakko{\vec A}$は線形写像である。

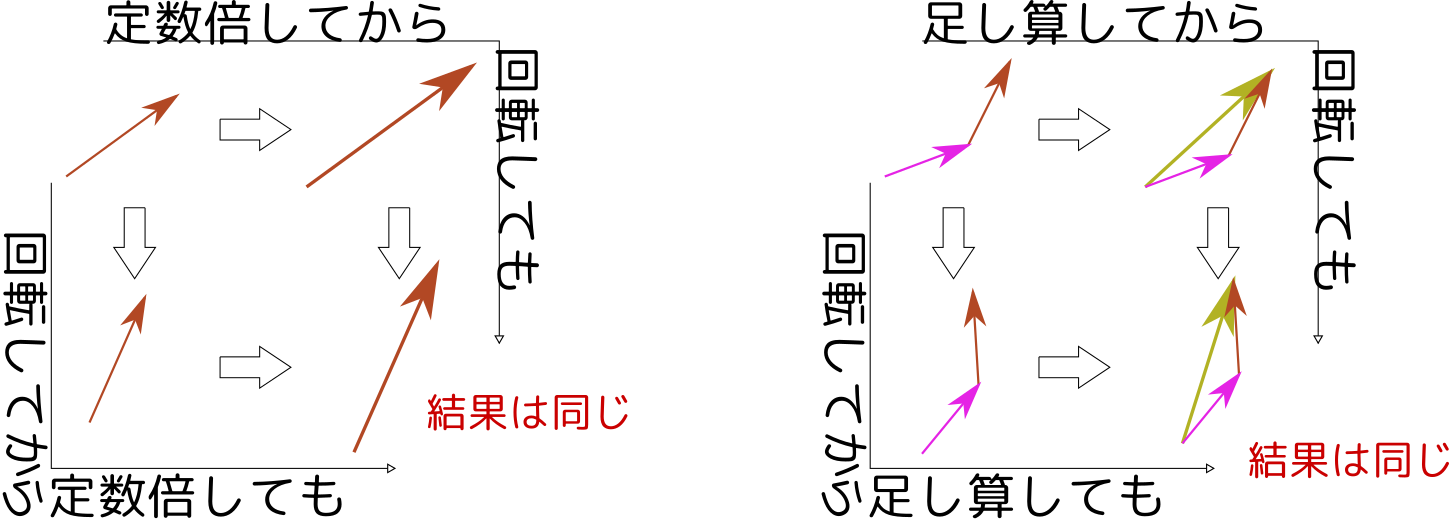
　すなわち、 \begin{align} R\kakko{\lambda_1\vec A_1+\lambda_2\vec A_2} =\lambda_1 R\kakko{\vec A_1}+\lambda_2 R\kakko{\vec A_2} \end{align} が成り立つ。ゆえに行列で表現できる。

　ここで行う回転は、実際に平面上にあるベクトルが向きを変えるという、物理的現象である。

わざわざこう断ったのは、物理的実体は変化しない単なる座標変換も「回転」という言葉を使って表現することがあるからである。

　回転を数式の上ではどのように扱うべきかを解説する。

　ベクトルの回転を表現してみよう。 回転を実現するには、

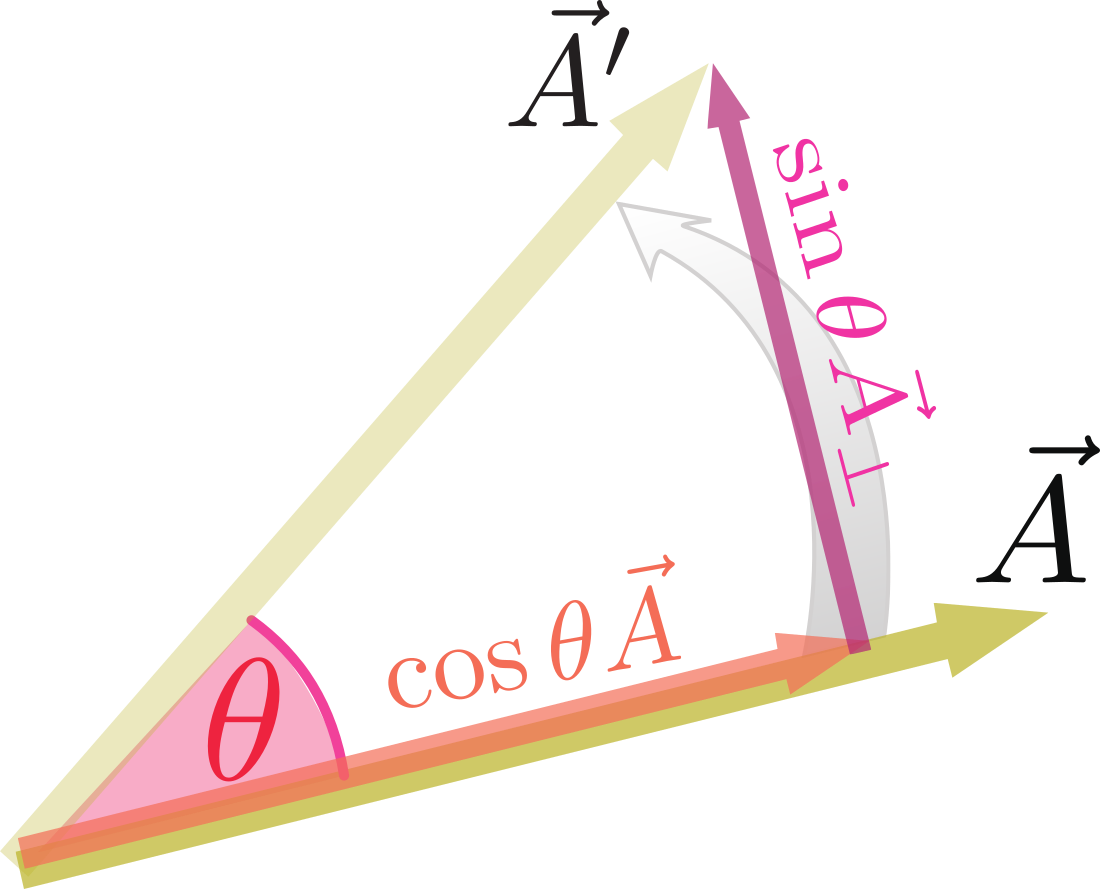
のように、元のベクトルの長さを$\cos \thetacol{\theta}$倍にしたもの（$\cos\thetacol{\theta}\vec A$）に、元のベクトルを90度（${\pi\over 2}$rad）倒して（このベクトルを${\vec A_{\Lsh}}$と書くことにする）長さを$\sin \thetacol{\theta}$倍にした、$\sin\thetacol{\theta}\vec A_{\Lsh}$を足す、という操作を行う。

ここでは90度倒すことを表す記号を「$\Lsh$」にした（一般的な記号ではない）。倒す方向は、反時計回り。平面の回転では「正の回転」を反時計回り、「負の回転」を時計回りとすることが多い。北極側から見た地球の自転は反時計回りで、正の回転である。

　そこでまず反時計周りの90度（${\pi\over 2}$rad）回転を考えることにしよう。

　$\vec A_{\Lsh}$の成分を

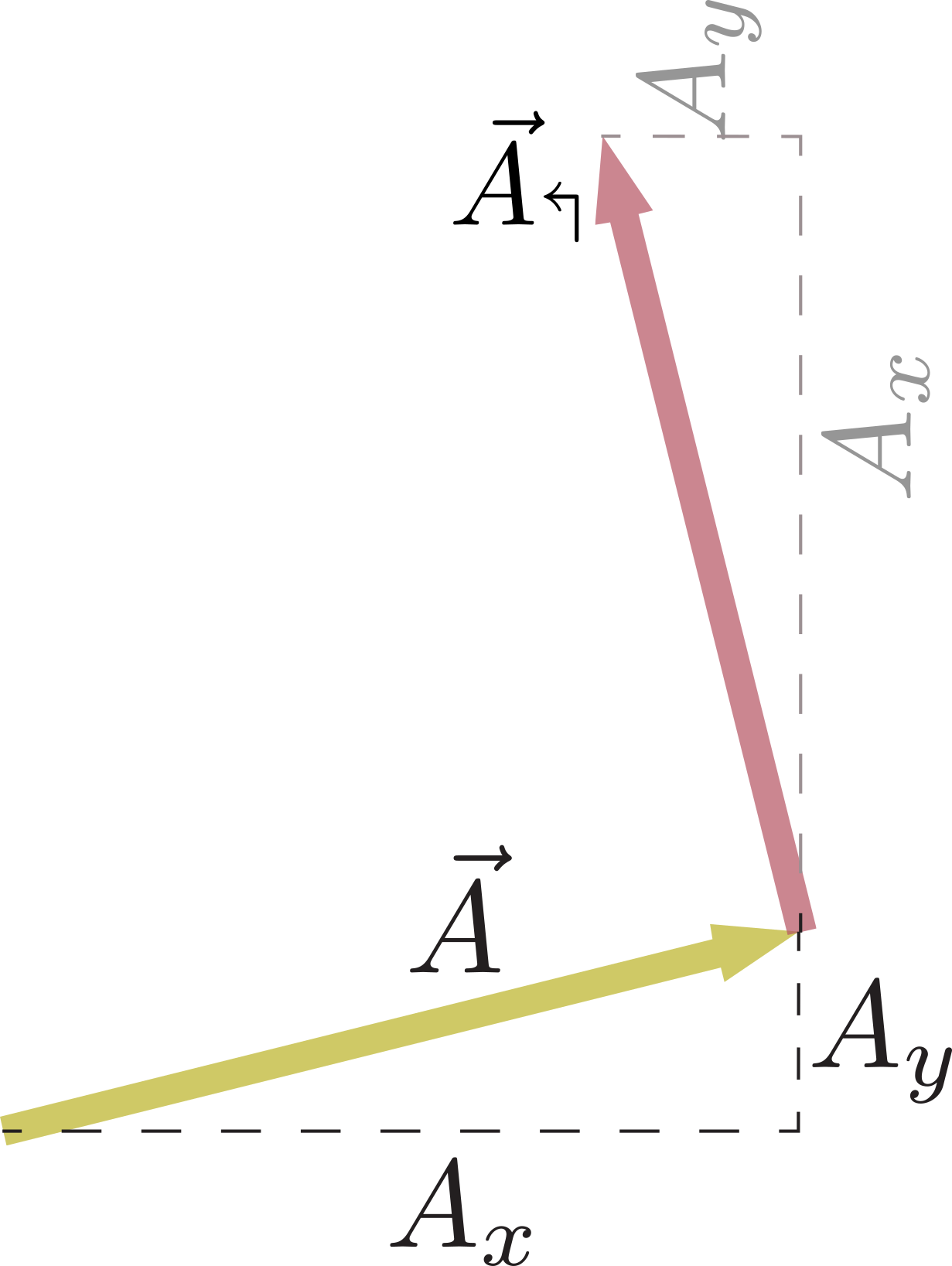
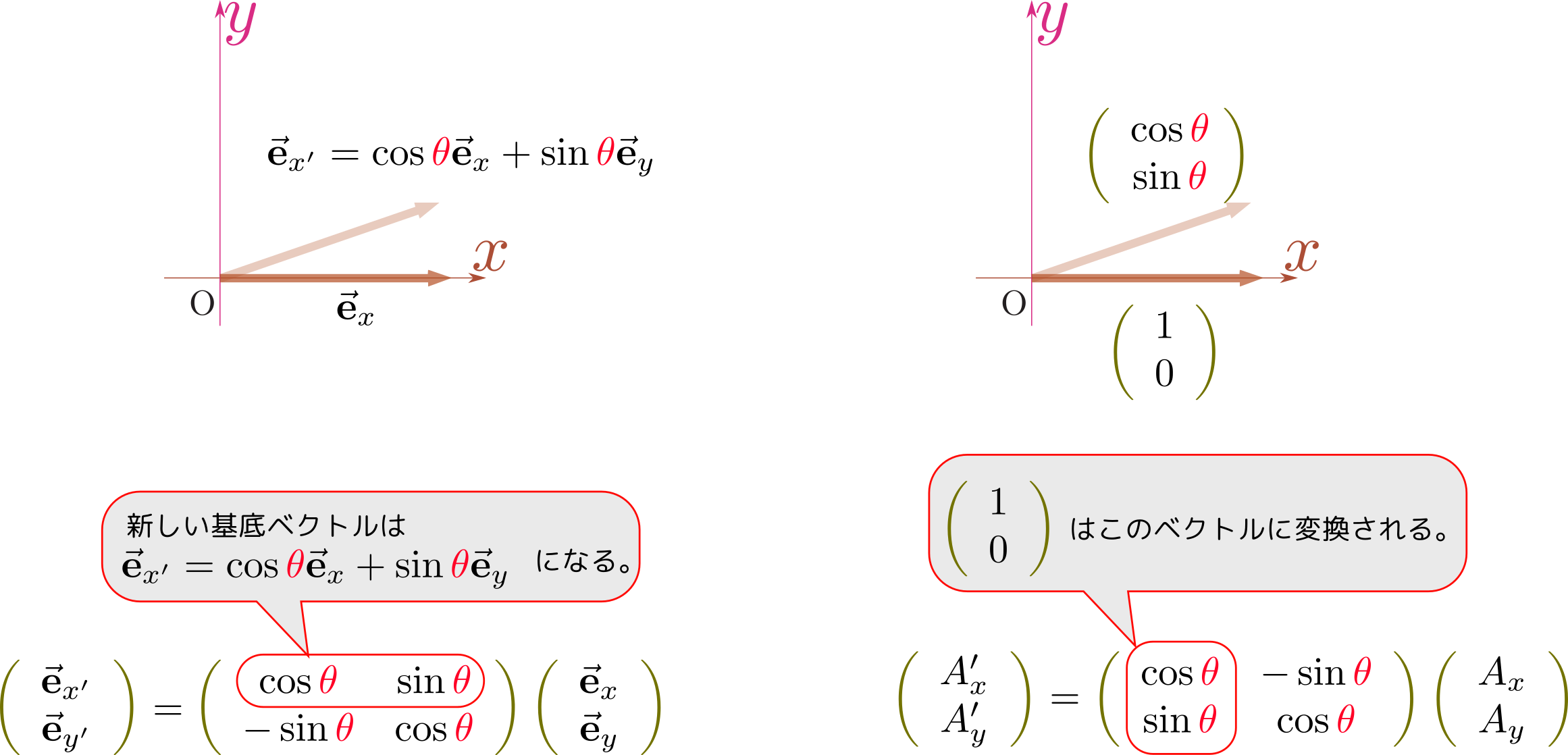
のように考えることで、「回転後の$\xcol{x}$成分は元の$\ycol{y}$成分（$A_y$）の符号を変えたもの、回転後の$\ycol{y}$成分は元の$\xcol{x}$成分（$A_x$）」という関係がわかる。「回転後のベクトルを、古い座標系でみたときの成分」が並ぶ位置が二つの変換では違うのである。

この1枚の図だけでそれを言って大丈夫なのか、と心配な人は何枚も図を描いてどのような場合でもこうなることを確認しよう。

　すなわち成分の変化は$\mtx[c]{A_x\\A_y}\to \mtx[c]{-A_y\\A_x}$であり、回転の結果は \begin{equation} \vec A_{\Lsh}=\goverbrace{-A_y}^{A_x\to}\ve_x+\goverbrace{A_x}^{A_y\to}\ve_y\label{chokkakukaiten} \end{equation} である。

　あるいはこれを

のように、$\mtx[c]{\ve_x\\\ve_y}\to \mtx[c]{\ve_y\\ -\ve_x}$という置き換えをした結果ベクトルが回転したと考えてもよい。

$\mtx[c]{A_x\\A_y}\to \mtx[c]{-A_y\\A_x}$と$\mtx[c]{\ve_x\\\ve_y}\to \mtx[c]{\ve_y\\ -\ve_x}$で符号の付く位置が違うことに注意（だが、これでいい）。

　こう考えても結果は \begin{equation} \vec A_{\Lsh}=A_x\goverbrace{\ve_y}^{\ve_x→}+A_y\goverbrace{(-\ve_x)}^{\ve_y→}=-A_y\ve_x+A_x\ve_y \end{equation} となる。

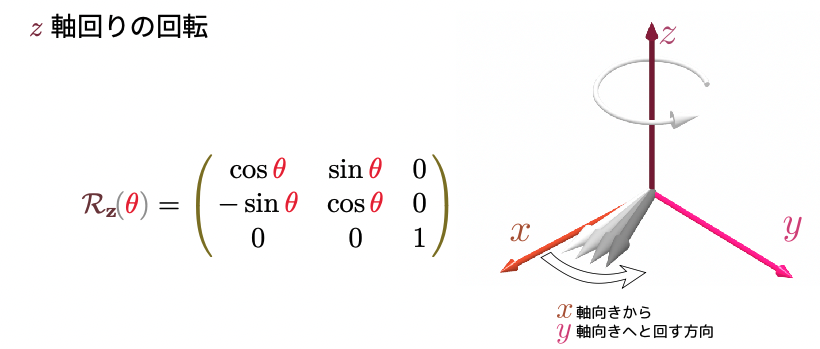
　${\pi\over 2}$の回転は上の通りであったので、角度$\theta$の回転を「元のベクトル$\vec A$の$\cos\thetacol{\theta}$倍に、$\vec A_{\Lsh}$の$\sin\thetacol{\theta}$倍を足す」という操作で実現してみると、 \begin{align} \mtx[c]{A'_x\\A'_y} =&\cos \thetacol{\theta}\goverbrace{\mtx[c]{A_x\\A_y}}^{\vec A}+\sin\thetacol{\theta}\goverbrace{\mtx[c]{-A_y\\A_x}}^{\vec A_{\Lsh}} \nonumber\\ =&\mtx[cc]{\cos \thetacol{\theta}&0\\0&\cos\thetacol{\theta}}\mtx[c]{A_x\\A_y}+ \mtx[cc]{0&-\sin\thetacol{\theta}\\\sin \thetacol{\theta}&0}\mtx[c]{A_x\\A_y}\nonumber\\ =& \mtx{\cos\thetacol{\theta}&-\sin \thetacol{\theta}\\\sin \thetacol{\theta}&\cos\thetacol{\theta}}\mtx[c]{A_x\\A_y} \label{seibunrot} \end{align} となる。

加法定理

　角度$\thetacol{\theta}$の回転を行ってから角度$\phicol{\phi}$の回転を行うという操作は（2次元で考える限り）「角度$\thetacol{\theta}+\phicol{\phi}$の回転」と同じ操作である。「行列は操作を表現したもの」なので、「二つの操作の合成」は行列の掛算で計算できる。やってみると、 \begin{align} & \mtx{ \cos \phicol{\phi}&-\sin\phicol{\phi}\\ \sin \phicol{\phi}&\cos\phicol{\phi} } \mtx{ \cos \thetacol{\theta}&-\sin\thetacol{\theta}\\ \sin \thetacol{\theta}&\cos\thetacol{\theta} }\nonumber\\ =&\mtx{ \cos \phicol{\phi}\cos\thetacol{\theta} -\sin \phicol{\phi}\sin\thetacol{\theta}& -\cos \phicol{\phi}\sin\thetacol{\theta} -\sin \phicol{\phi}\cos\thetacol{\theta}\\ \sin \phicol{\phi}\cos\thetacol{\theta} +\cos \phicol{\phi}\sin\thetacol{\theta}& \cos \phicol{\phi}\cos\thetacol{\theta} -\sin \phicol{\phi}\sin\thetacol{\theta} }\nonumber\\ =& \mtx{ \cos (\thetacol{\theta}+\phicol{\phi})&-\sin(\phicol{\phi}+\thetacol{\theta})\\ \sin (\thetacol{\theta}+\phicol{\phi})&\cos(\phicol{\phi}+\thetacol{\theta}) } \end{align} となって、三角関数の加法定理が出てくる。

　また、この結果を見ると、

• 「角度$\thetacol{\theta}$の回転を行ってから角度$\phicol{\phi}$の回転を行う」
• 「角度$\phicol{\phi}$の回転を行ってから角度$\thetacol{\theta}$の回転を行う」

が同じものだわかる。これは二つの行列$\mtx{\cos \phicol{\phi}&-\sin\phicol{\phi}\\\sin \phicol{\phi}&\cos\phicol{\phi}}$と$\mtx{\cos \thetacol{\theta}&-\sin\thetacol{\theta}\\\sin \thetacol{\theta}&\cos\thetacol{\theta}}$が可換であることを意味している。このため、2次元の回転は行列で表現されてはいるが、3次元以上に比べれば、かなり単純だとも言える。

成分の変換と基底の変換

成分の変換と基底の変換

成分の変換と基底の変換

　数式で回転を表現するには（実は回転に限らずもっと広い範囲の座標変換で言える）、次の図で表す二つの考え方がある。「成分の変換」と「基底の変換」である。

　どちらの場合でも、最初のベクトルは$\vec A=A_x\ve_x+A_y\ve_y$と表現されている。$A_x,A_y$が変化することによって回転が実現する、というのが左の図（成分の変換）、$\ve_x,\ve_y$の向きが変わることによって回転が実現する、というのが右の図（基底の変換）の考え方である。

　前から$\mtx[cc]{\ve_x&\ve_y}$を掛けることにより、ベクトル$\vec A$が \begin{equation} \vec A=\mtx[cc]{\ve_x&\ve_y}\mtx[c]{A_x\\ A_y}~~~\to~~~ \vec A'=\mtx[cc]{\ve_x&\ve_y}\mtx{\cos\thetacol{\theta}&-\sin \thetacol{\theta}\\\sin \thetacol{\theta}&\cos\thetacol{\theta}}\mtx[c]{A_x\\A_y} \end{equation} のように$\vec A'$に変換されるわけだが、この式を \begin{equation} \vec A'=\mtx[cc]{\ve_x&\ve_y}\gunderbrace{\mtx{\cos\thetacol{\theta}&-\sin \thetacol{\theta}\\\sin \thetacol{\theta}&\cos\thetacol{\theta}}\mtx[c]{A_x\\A_y}}_{\mtx[c]{A'_x\\A'_y}} \end{equation} と考えれば成分が変換されたということになるし、 \begin{equation} \vec A'= \gunderbrace{\mtx[cc]{\ve_x&\ve_y} \mtx{\cos\thetacol{\theta}&-\sin \thetacol{\theta}\\\sin \thetacol{\theta}&\cos\thetacol{\theta}} }_{\mtx[cc]{\ve_{x'}& \ve_{y'}}} \mtx[c]{A_x\\A_y} \label{Adashehenken} \end{equation} と考えれば基底ベクトルが変換されたということになる。この式は転置して書くと \begin{align} \vec A'= \mtx[cc]{A_x& A_y} \gunderbrace{ \mtx{\cos\thetacol{\theta}&\sin \thetacol{\theta}\\-\sin \thetacol{\theta}&\cos\thetacol{\theta}}\mtx[c]{\ve_x\\ \ve_y}}_{\mtx[c]{\ve_{x'}\\ \ve_{y'}}} \end{align} となるので、成分と基底を列ベクトルで表現することにした場合の、「成分を変換するための行列」と「基底ベクトルを変換するための行列」は互いに転置を取った関係であることに注意しよう。

となって、行列が転置された並び方になっていればこそ、この二つの変換が同じ回転を表現できていることがわかる。「回転後のベクトルを、古い座標系でみたときの成分」が並ぶ位置が二つの変換では違うのである。

前回の感想・コメントシートから 行列の転置と回転の行列

行列の転置と回転の行列

　ここで「行列の転置」について説明しておく。「転置する（縦のものを横にする）」という操作は、行列にとっては \begin{align} \mtx[ccc]{a&b&c\\ d&e&f}\to \mtx[cc]{a&d\\b&e\\c&f} \end{align} のように、行と列を入れ替える操作である。これにより、$n\times m$行列は$m\times n$行列に変わる。正方行列である場合は転置しても行数と列数は変わらない。

　転置という操作は$\mt{A^t}$のようにtという上付き添字をつけて表す。転置しても元と同じ行列（$\mt{A^t}=\mt{A}$を満たす行列）を「対称行列(symmetric matrix)」、逆に転置すると符号が変わる行列（$\mt{A}^t=-\mt{A}$を満たす行列）を「反対称行列(antisymmetric matrix)」と言う。対称行列にしろ反対称行列にしろ、正方行列でなければ意味がない言葉である。

　転置が以下の性質を満たすことはすぐにわかる。

　最後の4.だけが少し考えないとわからないかもしれないが、行列の掛け算が \begin{align} \mtx[c]{ \yokovec{\xcol{\vec v_1}}\\ \yokovec{\xcol{\vec v_2}}\\ \vdots\\ \yokovec{\xcol{\vec v_n}} }\mtx[cccc]{\nagatatevec{\ycol{\vec w_1}}&\nagatatevec{\ycol{\vec w_2}}&\cdots&\nagatatevec{\ycol{\vec w_n}}} =\mtx[cccc]{ \xcol{\vec v_1}\cdot \ycol{\vec w_1}&\xcol{\vec v_1}\cdot \ycol{\vec w_2}&\cdots&\xcol{\vec v_1}\cdot \ycol{\vec w_n}\\ \xcol{\vec v_2}\cdot \ycol{\vec w_1}&\xcol{\vec v_2}\cdot \ycol{\vec w_2}&\cdots&\xcol{\vec v_2}\cdot \ycol{\vec w_n}\\ \vdots&\vdots&\ddots&\vdots\\ \xcol{\vec v_n}\cdot \ycol{\vec w_1}&\xcol{\vec v_n}\cdot \ycol{\vec w_2}&\cdots&\xcol{\vec v_n}\cdot \ycol{\vec w_n}\\ } \end{align} であり、これを転置するということは、 \begin{align} \mtx[c]{ \yokovec{\ycol{\vec w_1}}\\ \yokovec{\ycol{\vec w_2}}\\ \vdots\\ \yokovec{\ycol{\vec w_n}} }\mtx[cccc]{\nagatatevec{\xcol{\vec v_1}}&\nagatatevec{\xcol{\vec v_2}}&\cdots&\nagatatevec{\xcol{\vec v_n}}} =\mtx[cccc]{ \ycol{\vec w_1}\cdot \xcol{\vec v_1}&\ycol{\vec w_1}\cdot \xcol{\vec v_2}&\cdots&\ycol{\vec w_1}\cdot \xcol{\vec v_n}\\ \ycol{\vec w_2}\cdot \xcol{\vec v_1}&\ycol{\vec w_2}\cdot \xcol{\vec v_2}&\cdots&\ycol{\vec w_2}\cdot \xcol{\vec v_n}\\ \vdots&\vdots&\ddots&\vdots\\ \ycol{\vec w_n}\cdot \xcol{\vec v_1}&\ycol{\vec w_n}\cdot \xcol{\vec v_2}&\cdots&\ycol{\vec w_n}\cdot \xcol{\vec v_n}\\ } \end{align} とすることだ（このように行列の順番を変えないと$\xcol{\vec v}$と$\ycol{\vec w}$の内積を取る形にならない）と気づけば、転置するときに行列の掛け算の順番が入れ替わることは納得できるだろう。

　前項で作った角度$\thetacol{\theta}$の回転の行列$\mt{R}\kakko{\theta}=\mtx{\cos\thetacol{\theta}&-\sin \thetacol{\theta}\\\sin \thetacol{\theta}&\cos\thetacol{\theta}}$は、転置すると$\mt{R^t}\kakko{\theta}=\mtx{\cos\thetacol{\theta}&\sin \thetacol{\theta}\\-\sin \thetacol{\theta}&\cos\thetacol{\theta}}$となり、これは角度$-\thetacol{\theta}$の回転の行列である。つまり、$\mt{R^t}$は$\mt{R}$の逆行列である。これは偶然でもなんでもない。行列$\mt{R}$は、$\ve_x,\ve_y$を回した結果の列ベクトル$\ve_{x\thetacol{\theta}},\ve_{y\thetacol{\theta}}$を並べたものと解釈できるからなのである。 \begin{align} \ve_{x\thetacol{\theta}}\equiv& \mtx{\cos\thetacol{\theta}&-\sin \thetacol{\theta}\\ \sin \thetacol{\theta}&\cos\thetacol{\theta}}\mtx[c]{1\\0} = \mtx[c]{\cos\thetacol{\theta}\\\sin \thetacol{\theta}}\\ \ve_{y\thetacol{\theta}}\equiv& \mtx{\cos\thetacol{\theta}&-\sin \thetacol{\theta}\\\sin \thetacol{\theta}&\cos\thetacol{\theta}}\mtx[c]{0\\1} = \mtx{-\sin \thetacol{\theta}\\\cos\thetacol{\theta}} \end{align}

　この二つのベクトルは「$\mtx[c]{1\\0}$を回した結果」と「$\mtx[c]{0\\1}$を回した結果」であり、このベクトルを並べると$\mt{R}$ができる。ここで、 \begin{align} \gunderbrace{\mtx[c]{\yokovec{\ve_{x\thetacol{\theta}}}\\ \yokovec{\ve_{y\thetacol{\theta}}}}}_{\mt{R^t}}\gunderbrace{\mtx[c@{\,}c]{\nagatatevec{\ve_{x\thetacol{\theta}}}&\nagatatevec{\ve_{y\thetacol{\theta}}}}}_{\mt{R}} =\mtx{ \ve_{x\thetacol{\theta}}\cdot\ve_{x\thetacol{\theta}} &\ve_{x\thetacol{\theta}}\cdot\ve_{y\thetacol{\theta}}\\ \ve_{y\thetacol{\theta}}\cdot\ve_{x\thetacol{\theta}} &\ve_{y\thetacol{\theta}}\cdot\ve_{y\thetacol{\theta}} } \end{align} のようにしてみると、$\mt{R^t}\mt{R}=\mt{I}$がすぐわかる（回転の前の$\ve_x,\ve_y$が$\ve_i\cdot\ve_j=\delta_{ij}$を満たしていたのだから、回転後も満たしているのは当然だ）。

　以上は平面でなく任意の次元の「回転を表す行列」に関して言える。一般に、$\mt{R^t}\mt{R}=\mt{I}$を満たす行列$\mt{R}$を「直交行列(orthogonal matrix)」と呼ぶ。名前に「直交」が入っているのは「行列を列ベクトルの組とみたとき、列ベクトルは相互に直交している（内積が0）」を意味している。

答えはここにある。考えて答えがわかったらクリック。

たとえば、$\mtx{1&0\\0&-1}$。これは直交する2本の列ベクトルを並べているが、回転では得られない（上下反転の行列）。

基本変形 微小角度の回転と生成子

微小角度の回転と生成子

微小角度の回転の無限回繰り返し

　ここで$\cos \thetacol{\theta}$と$\sin \thetacol{\theta}$のテイラー展開 \begin{align} \cos\thetacol{\theta}&=\sum_{n=0}^\infty {(-1)^n\over (2n)!}\thetacol{\theta}^{2n}=1-{1\over 2}\thetacol{\theta}^2+{1\over 4!}\thetacol{\theta}^4-\cdots \\ \sin\thetacol{\theta}&=\sum_{n=0}^\infty {(-1)^n\over (2n+1)!}\thetacol{\theta}^{2n+1}=\thetacol{\theta}-{1\over 3!}\thetacol{\theta}^3+{1\over 5!}\thetacol{\theta}^5-\cdots \end{align} をこの式に代入すると、 \begin{equation} \mtx{\cos\thetacol{\theta}&-\sin \thetacol{\theta}\\\sin \thetacol{\theta}&\cos\thetacol{\theta}} = \mtx{1&0\\0&1} +\mtx{0&-\thetacol{\theta}\\\thetacol{\theta}&0} +\mtx{\textstyle-{\thetacol{\theta}^2\over 2}&0\\0&\textstyle-{\thetacol{\theta}^2\over 2}} +\mtx{0&\textstyle{\thetacol{\theta}^3\over 3!}\\\textstyle-{\thetacol{\theta}^3\over 3!}&0} +\cdots \end{equation} のようになるが、この展開の規則性をよくみると、 \begin{equation} \mtx{\cos\thetacol{\theta}&-\sin \thetacol{\theta}\\\sin \thetacol{\theta}&\cos\thetacol{\theta}} =\sum_{\ycol{n}=0}^\infty {1\over \ycol{n}!}\thetacol{\theta}^\ycol{n} {\mtx{0&-1\\1&0}}^{\ycol{n}} \end{equation} とまとめることができる。

　指数関数のテイラー展開 \begin{equation} \exp\xcol{x}=\sum_{\ycol{n}}{1\over\ycol{n}!}\xcol{x}^{\ycol{n}} \end{equation} を思い出し、$\xcol{x}$が行列であってもこの式が使えると考えると、 \begin{equation} \mtx{\cos\thetacol{\theta}&-\sin \thetacol{\theta}\\\sin \thetacol{\theta}&\cos\thetacol{\theta}} =\exp{\mtx{0&-\thetacol{\theta}\\\thetacol{\theta}&0}} =\sum_{\ycol{n}=0}^\infty {1\over \ycol{n}!}\thetacol{\theta}^\ycol{n} {\mtx{0&-1\\1&0}}^{\ycol{n}} \end{equation} と書くことができる。

　指数関数は、 \begin{equation} \exp\xcol{x}=\lim_{N\to\infty}\left(1+{\xcol{x}\over N}\right)^N \end{equation} のように、極限を使って定義することもできた。同様に、 \begin{equation} \exp\mtx{0&-\thetacol{\theta}\\\thetacol{\theta}&0} =\lim_{N\to\infty}\left(\mtx{1&0\\0&1} + \mtx{0&-{\thetacol{\theta}\over N}\\{\thetacol{\theta}\over N}&0} \right)^N \end{equation} と考えることもできる。ここに現れた行列$\mtx{1&0\\0&1}+\mtx{0&-{\thetacol{\theta}\over N}\\{\thetacol{\theta}\over N}&0}$の意味は、元のベクトル$+$元のベクトルを${\pi\over 2}$回して長さを${\thetacol{\theta}\over N}$倍したベクトル}という演算であり、これは「微小角度${\thetacol{\theta}\over N}$の回転」に対応している。つまり「微小角度${\thetacol{\theta}\over N}$の回転」を$N$回繰り返すことで角度$\thetacol{\theta}$の回転を作っている。

　後での都合上$\exp$の肩に$-\I$を入れて、 \begin{align} \mt{R\kakko{\theta}}=\exp\kakko{-\I\thetacol{\theta}\mtx{0&-\I\\\I&0}}\label{Rexp} \end{align} のように回転行列を表したときの行列 \begin{align} \mt{L}=\mtx{0&-\I\\\I&0} \end{align} を、「回転の生成子」と呼ぶ。

　これに限らず「微小変換」を考えて、その微小変換が（微小なパラメータを$\thetacol{\Delta \theta}$として） \begin{align} \vec V\to \left( \mt{I}-\I\thetacol{\Delta\theta}\mt{G} \right)\vec V \end{align} と書けるとき、$\mt{G}$を変換の「生成子(generator)」と呼ぶ。パラメータが微小でない場合は、変換は$\vec V\to \exp\left[-\I\thetacol{\theta}\mt{G}\right]$となる。

行列の転置と回転の行列 ３次元回転

３次元回転

3次元回転の行列による表現

　3次元の回転を考えるために、以下に示すような3種類の2次元回転をまず考えることにしよう。以下では \begin{align} \vec A=\mtx[ccc]{A_x& A_y & A_z}\mtx[c]{\ve_x\\\ve_y\\\ve_z}\to \vec A'=\mtx[ccc]{A_x& A_y &A_z}\mt{\cal R}\mtx[c]{\ve_x\\\ve_y\\\ve_z} \end{align} と書いたとき（基底ベクトルを列ベクトルとしたとき）の行列$\mt{\cal R}$について考えていくことにする。わざわざこう書いたのは、 \begin{align} \vec A=\mtx[ccc]{\ve_x& \ve_y & \ve_z}\mtx[c]{A_x\\A_y\\A_z}\to \vec A'=\mtx[ccc]{\ve_x& \ve_y &\ve_z}\mt{R}\mtx[c]{A_x\\A_y\\A_z} \end{align} と書いたとき（成分ベクトルを列ベクトルとしたとき）の行列$\mt{R}$と区別するためである（実は$\mt{R^t}=\mt{\cal R}$）。

　本講義では、成分を変換する行列は$\mt{R}$、基底を変換する行列は$\mt{\cal R}$とする。

　まず、$\zcol{z}$軸周りの回転は$\xcol{x}\ycol{y}$平面での回転だから、2次元の回転と同じになる。

のように行列で表現される。$\zcol{z}$成分に対しては何もしないので、その部分は1になっている。念のため行列を使わずに書き下すと \begin{align} \ve_{x'}=\cos\thetacol{\theta}\ve_x+\sin \thetacol{\theta}\ve_y,~~ \ve_{y'}=-\sin\thetacol{\theta}\ve_y+\cos \thetacol{\theta}\ve_y,~~\ve_{z'}=\ve_z \end{align} である。

同様に、$\xcol{x}$軸回りの回転と$\ycol{y}$軸回りの回転を表現すると以下のようになる。

　ここで重要なことは、これらの行列は互いに可換ではないということである。具体的に計算してみると、 \begin{align} & \goverbrace{\mtx[ccc]{1&0&0\\ 0&\cos \thetacol{\theta}&\sin \thetacol{\theta}\\ 0&-\sin \thetacol{\theta}&\cos \thetacol{\theta}}}^{\mt{{\cal R}_x\kakko{\thetacol{\theta}}}}\, \goverbrace{ \mtx[ccc]{ \cos \phicol{\phi}&\sin \phicol{\phi}&0\\ -\sin \phicol{\phi}&\cos \phicol{\phi}&0\\ 0&0&1} }^{\mt{{\cal R}_z\kakko{\phicol{\phi}}}} \nonumber\\ =&\mtx[ccc]{ \cos \phicol{\phi}&\sin \phicol{\phi}&0\\ -\cos\thetacol{\theta}\sin \phicol{\phi}&\cos\thetacol{\theta}\cos \phicol{\phi}&\sin \thetacol{\theta}\\ \sin \thetacol{\theta}\sin \phicol{\phi}&-\sin \thetacol{\theta}\cos \phicol{\phi}&\cos \thetacol{\theta}} \end{align} と \begin{align} & \goverbrace{ \mtx[ccc]{ \cos \phicol{\phi}&\sin \phicol{\phi}&0\\ -\sin \phicol{\phi}&\cos \phicol{\phi}&0\\ 0&0&1} }^{\mt{{\cal R}_z\kakko{\phicol{\phi}}}} \goverbrace{\mtx[ccc]{1&0&0\\ 0&\cos \thetacol{\theta}&\sin \thetacol{\theta}\\ 0&-\sin \thetacol{\theta}&\cos \thetacol{\theta}}}^{\mt{{\cal R}_x\kakko{\thetacol{\theta}}}}\, \nonumber\\ =&\mtx[ccc]{ \cos \phicol{\phi}&\cos\thetacol{\theta}\sin \phicol{\phi}&\sin\thetacol{\theta}\sin \phicol{\phi}\\ -\sin \phicol{\phi}&\cos\thetacol{\theta}\cos \phicol{\phi}&\sin \thetacol{\theta}\cos \phicol{\phi}\\ 0&-\sin \thetacol{\theta}&\cos \thetacol{\theta}} \end{align} である。実際に何かを回してみても、

• $\xcol{x}$軸回りに$\thetacol{\theta}$回してから$\zcol{z}$軸回りに$\phicol{\phi}$回す
• $\zcol{z}$軸回りに$\phicol{\phi}$回してから$\xcol{x}$軸回りに$\thetacol{\theta}$回す

の結果は全く違う。

微小角度の回転と生成子 オイラー角

オイラー角

　さてここで当然「斜めの軸で回すのはどう表現するのか」という疑問が湧くことと思う。この疑問に関しては「上の回転を組み合わせれば、すべての回転は表現できるのでは？」という解答がありえるだろう。

　「組み合わせる」ということはもちろん、行列の掛算を行うということである。よく使われるのが「Euler角(Euler Angle)」（Eulerはカタカナ表記では「オイラー」）という3つのパラメータを使った行列の掛算で、基底の変換なら \begin{align} \goverbrace{ \mtx[ccc]{ \cos \psicol{\psi}&\sin \psicol{\psi}&0\\ -\sin \psicol{\psi}&\cos \psicol{\psi}&0\\ 0&0&1} }^{\mt{{\cal R}_z\kakko{\psicol{\psi}}}}\, \goverbrace{\mtx[ccc]{1&0&0\\ 0&\cos \thetacol{\theta}&\sin \thetacol{\theta}\\ 0&-\sin \thetacol{\theta}&\cos \thetacol{\theta}}}^{\mt{{\cal R}_x\kakko{\thetacol{\theta}}}}\, \goverbrace{ \mtx[ccc]{ \cos \phicol{\phi}&\sin \phicol{\phi}&0\\ -\sin \phicol{\phi}&\cos \phicol{\phi}&0\\ 0&0&1} }^{\mt{{\cal R}_z\kakko{\phicol{\phi}}}}\, \end{align} のような3つの行列の積で回転を表現する。この順の行列の積を使う場合は「ZXZのオイラー角による変換」と呼ぶ。行列の組み合わせは他にもXYZにしたりすることもある。

　この積は具体的に計算すると \begin{align} \mtx[ccc]{ \cos \psicol{\psi}\cos \phicol{\phi} -\sin \psicol{\psi}\cos \thetacol{\theta} \sin \phicol{\phi} & \cos \psicol{\psi} \sin \phicol{\phi}+\sin \psicol{\psi}\cos \thetacol{\theta}\cos \phicol{\phi} & \sin \psicol{\psi} \sin \thetacol{\theta} \\ -\sin \psicol{\psi}\cos \phicol{\phi}-\cos \psicol{\psi} \cos \thetacol{\theta} \sin \phicol{\phi} & -\sin \psicol{\psi} \sin \phicol{\phi}+\cos \psicol{\psi} \cos \thetacol{\theta}\cos \phicol{\phi} & \cos \psicol{\psi} \sin \thetacol{\theta}\\ \sin \thetacol{\theta}\sin \phicol{\phi} & -\sin \thetacol{\theta}\cos \phicol{\phi} & \cos \thetacol{\theta} } \end{align} となる。基底の変換ではなく成分の変換なら全体を転置すればよいので、 \begin{align} \mtx[ccc]{ \cos \psicol{\psi}\cos \phicol{\phi} -\sin \psicol{\psi}\cos \thetacol{\theta} \sin \phicol{\phi} & -\sin \psicol{\psi}\cos \phicol{\phi}-\cos \psicol{\psi} \cos \thetacol{\theta} \sin \phicol{\phi} & \sin \thetacol{\theta}\sin \phicol{\phi} \\ \cos \psicol{\psi} \sin \phicol{\phi}+\sin \psicol{\psi}\cos \thetacol{\theta}\cos \phicol{\phi} & -\sin \psicol{\psi} \sin \phicol{\phi}+\cos \psicol{\psi} \cos \thetacol{\theta}\cos \phicol{\phi} & -\sin \thetacol{\theta}\cos \phicol{\phi} \\ \sin \psicol{\psi} \sin \thetacol{\theta} & \cos \psicol{\psi} \sin \thetacol{\theta} & \cos \thetacol{\theta} } \end{align} となる。この行列は \begin{align} \goverbrace{ \mtx[ccc]{ \cos \phicol{\phi}&-\sin \phicol{\phi}&0\\ \sin \phicol{\phi}&\cos \phicol{\phi}&0\\ 0&0&1} }^{\mt{{R}_z\kakko{\phicol{\phi}}}}\, \goverbrace{\mtx[ccc]{1&0&0\\ 0&\cos \thetacol{\theta}&-\sin \thetacol{\theta}\\ 0&\sin \thetacol{\theta}&\cos \thetacol{\theta}}}^{\mt{{R}_x\kakko{\thetacol{\theta}}}}\, \goverbrace{ \mtx[ccc]{ \cos \psicol{\psi}&-\sin \psicol{\psi}&0\\ \sin \psicol{\psi}&\cos \psicol{\psi}&0\\ 0&0&1} }^{\mt{{R}_z\kakko{\psicol{\psi}}}}\, \end{align} と表現することもできる（ゆえに成分の変換として考えるときは、$\phicol{\phi}\to\thetacol{\theta}\to\psicol{\psi}$の順番が逆になる（成分の変換と基底の変換、どちらを使っているのかに注意）。

　この場合は「（物体に固定された座標系の）基底の変換」の方が「（座標系がくくりつけられている）物体の回転」を表現して いることになる。

　なお、webClassに情報を載せていますが、木と金の11:50〜12:50の間、オンラインオフィスアワーとしてzoomを開いてます。質問や相談などがある人は来て話してください。参加者が少ないので、物理系１年生向けのオフィスアワーと合同になってます。

３次元回転 受講者の感想・コメント

受講者の感想・コメント

オイラー角