波の基本
波はどんな現象か
「波動」の分野はかなり生徒に嫌われることが多い。だが一方で音・光という身近な現象に引き寄せて語ることができるという点では、電磁気よりは親しみやすく教えることができるはずである。
では、波の何がそんなに難しいのかということを考えつつ、波動の基本について考えていこう。
振動が起こるための条件として重要なものが二つある。
- 復元力が働く どこかに「振動の中心」があって、その中心に戻そうとする力(復元力)が働いてないと振動は発生しない。たとえば振り子であれば「最下点」が「振動の中心」で、そこに戻すように重力がはたらく(正確には復元力は重力のうち糸に垂直な方向の分力)。
- 慣性がある 復元力が働いても、振動の中心で動きが止まってしまったらそこで運動は終わってしまう。中心に移動するときに速度を持って、その速度により「中心点を行き過ぎる」ことで振動が続く。
さらにその振動が「波」であるためには、
- 振動の状態が伝わること 空間のある場所で起こった振動が、時間的に遅れながら周囲に伝わっていく。
ことが必要である(一箇所で振動しているだけでは「波」とは呼ばない)。
以下の「波」では、どのような復元力が働いているか?水面の波(クリックすると答えがあります)
水が一部分だけ盛り上がっていたら、当然水面のその部分を「下げる」方向に、逆に水が一部分だけ窪んでいたら、水面のその部分を「上げる」方向に変化が起こることはわかるだろう。それが復元力である。音(クリックすると答えがあります)
音は「疎密波」と言われるように、空気の密度の変化の波である。「密」な部分は高圧となり、「疎」な部分は低圧となる。すると「高圧部分から低圧部分へ」という流れが発生し、「密」な部分からは空気が逃げ出し、「疎」な部分には空気が集まって、「粗密」を平均化しようという作用が働く。この作用が復元力となる。地震波(クリックすると答えがあります)
固体は変形されると元に戻ろうとする作用がある(典型的な例はバネである)。地球を構成する近くにも当然、その作用がある。↓は、波の進行の様子を表現するアプリである。まずはこれでじっくりと、波というのがどういう動きをするものかを実感しよう(ブラウザの「戻る」で戻ってくること)。
以下に文章による説明を入れるが、アニメーションを見ながら動きで理解しよう。
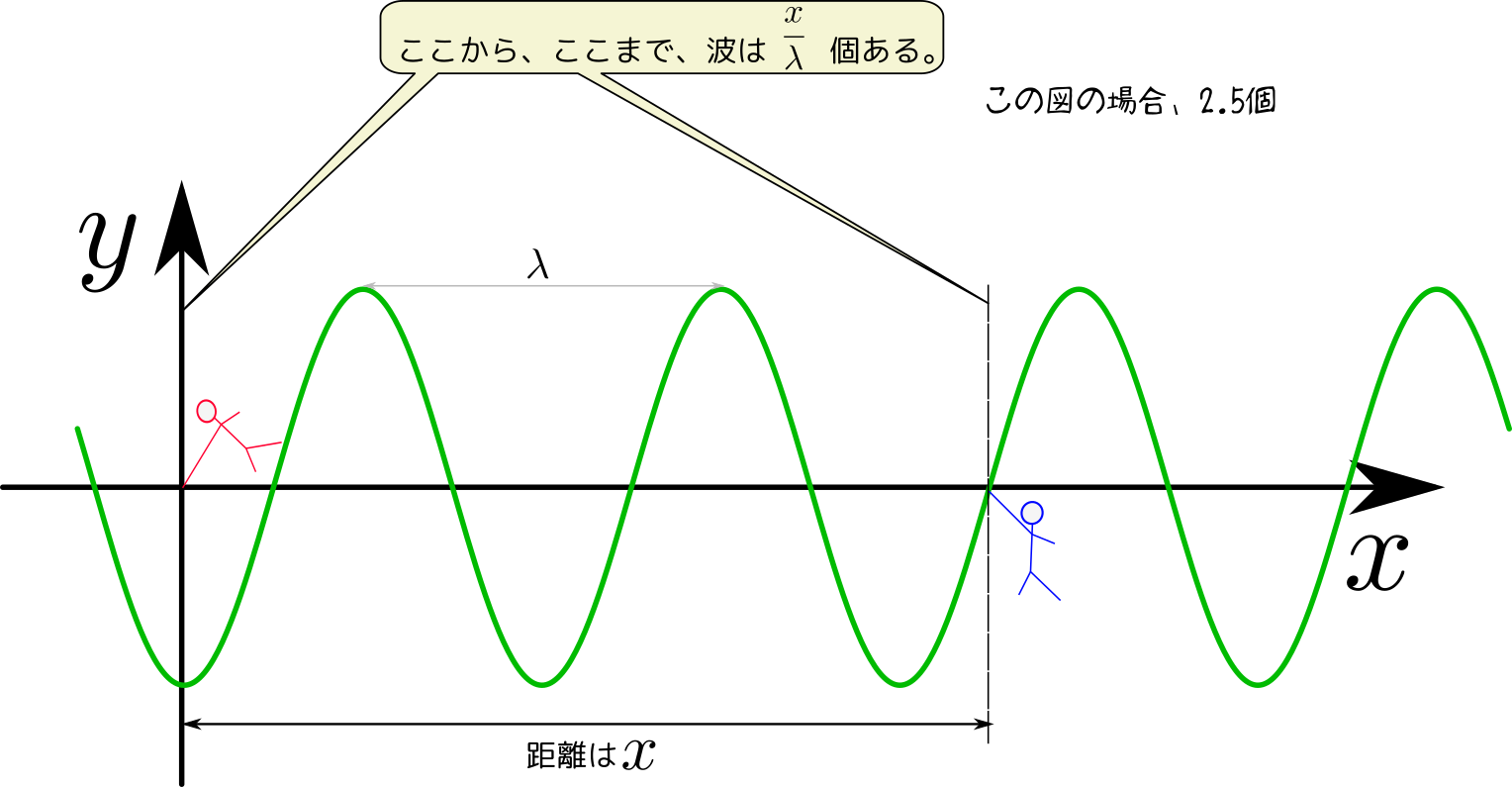
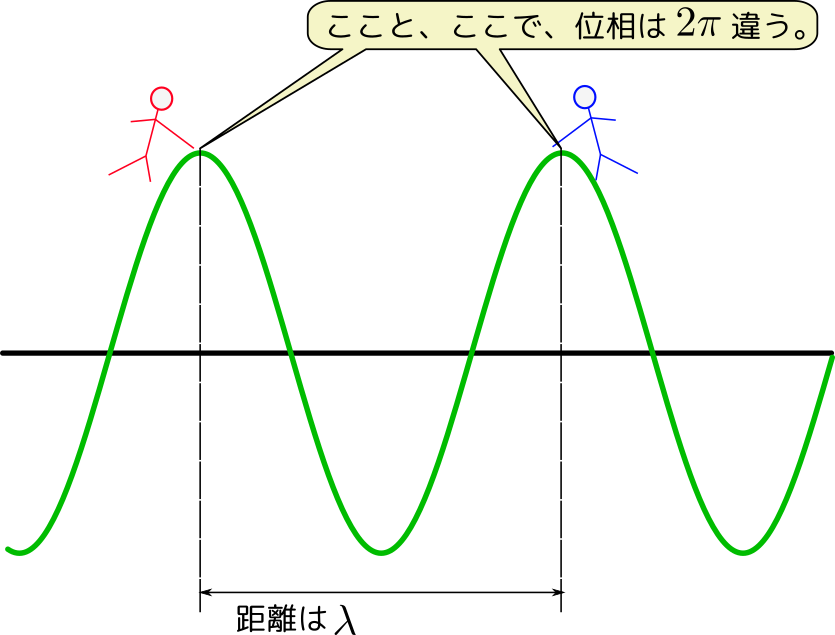
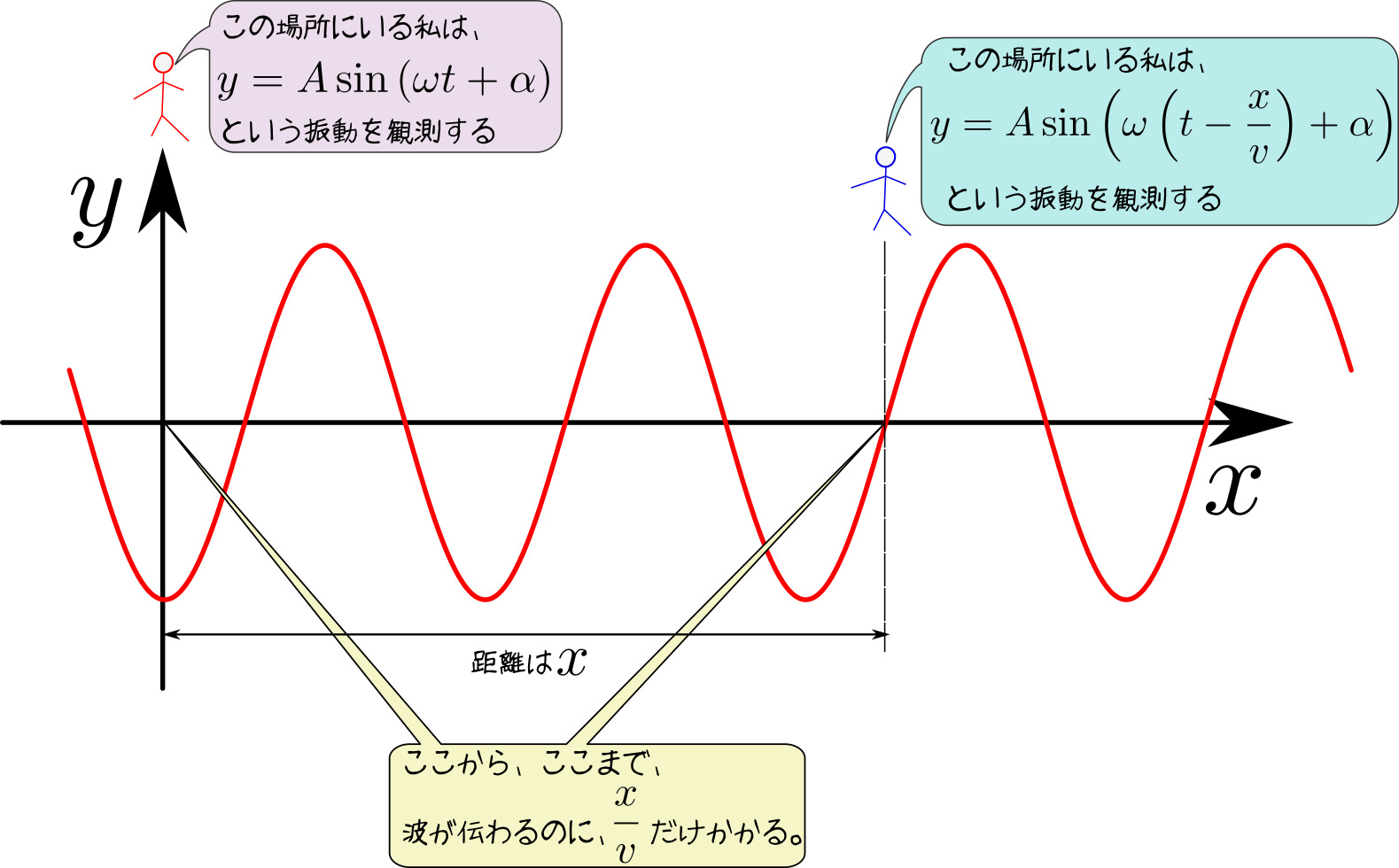
波が進行しているときの各媒質の速度を図に示すと以下のようになる。ここで$x$は場所を表す「座標」であり、$y$は波の媒質がつりあいの位置に対してどの程度動いているかを表す「変位」である。
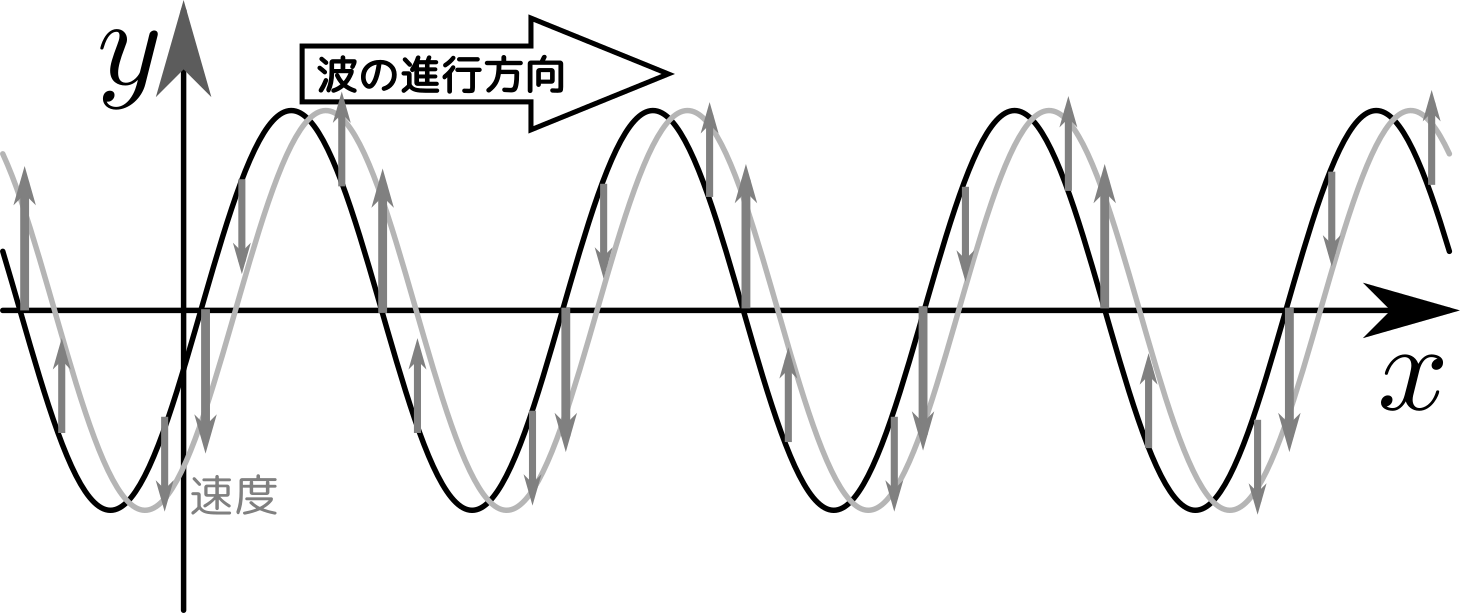
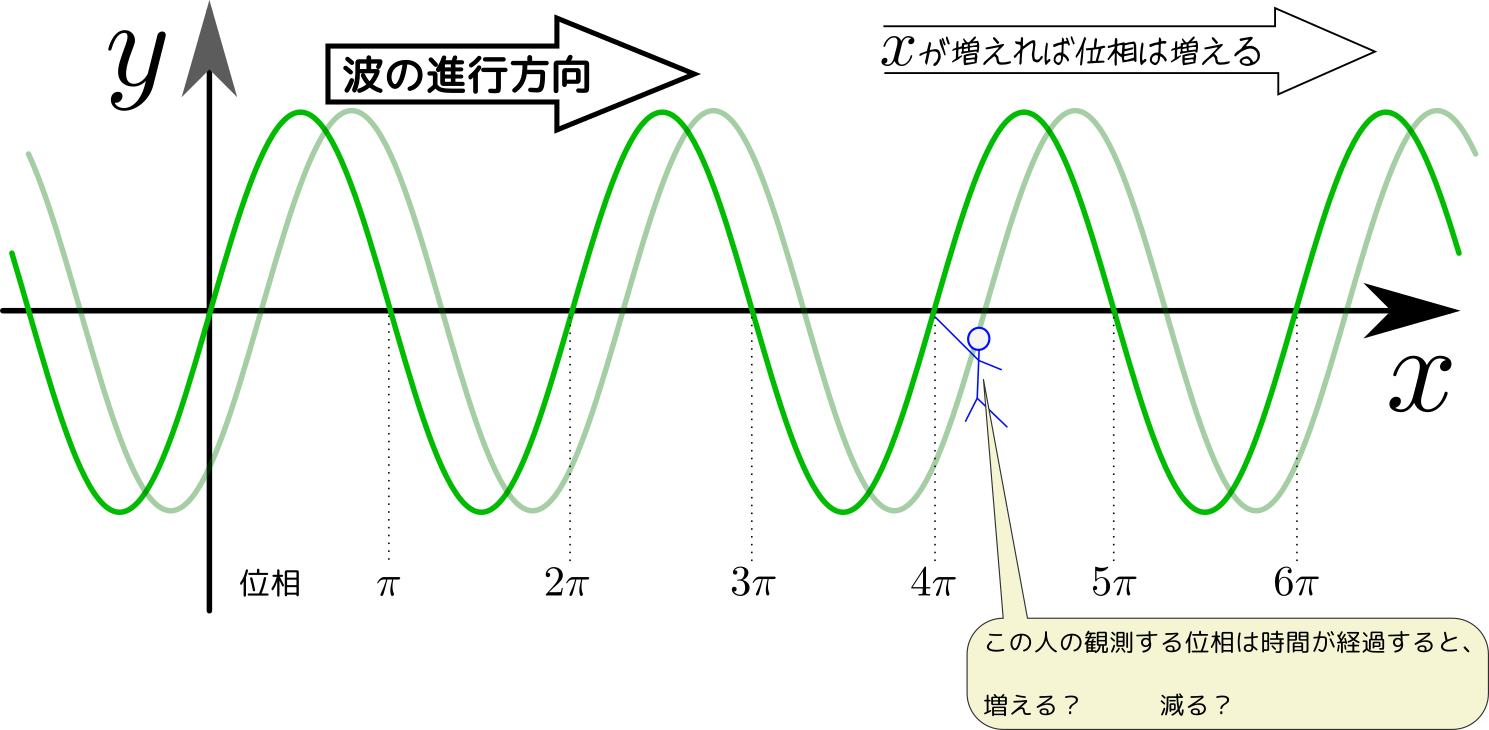
図の黒線が「波の現在位置」、灰色の線が「波のしばらく後の位置」なので、その「しばらく」の間にどう運動しているかを考えれば、速度の矢印が図のようになることは納得できる。
素朴な間違いとして「波の進行方向が右だから、その場所にいる媒質も右に運動している」というものもよくある。実際には、進行方向と媒質の振動方向は一般には一致しない(縦波では方向は一致するが、向きは一致しない)。
加速度(およびそれに比例する力)は、速度の変化の様子を見ればわかる。それは
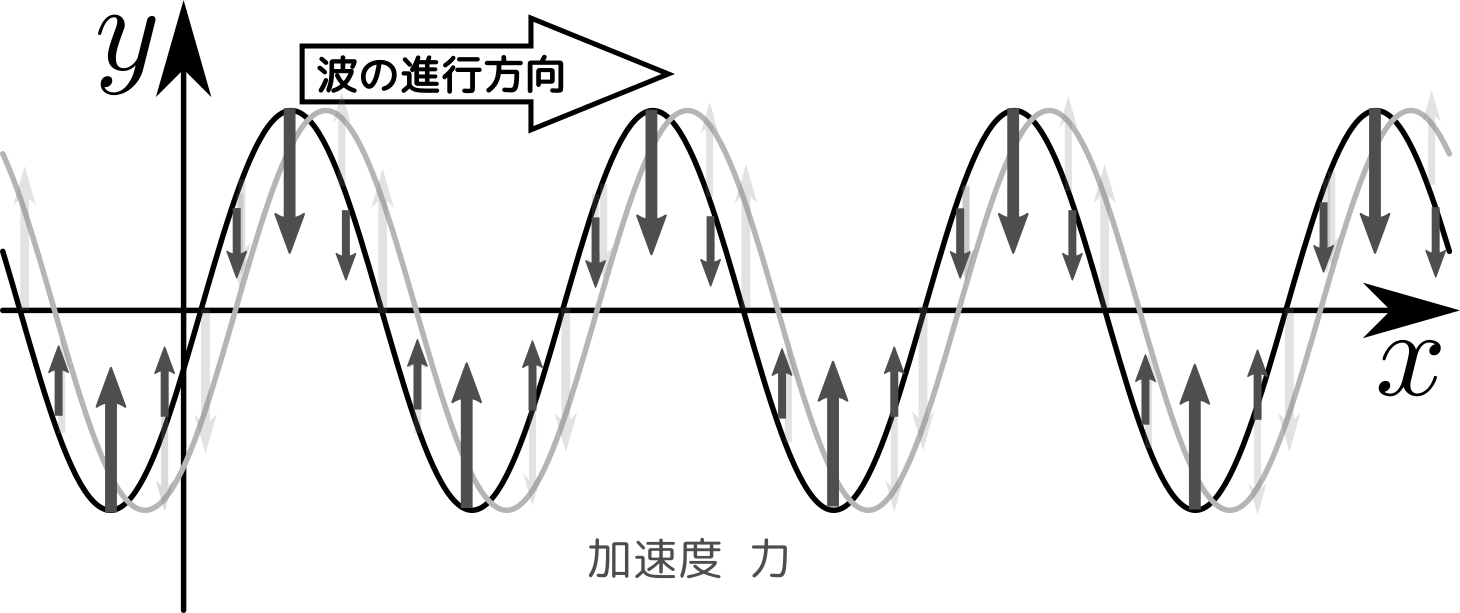
のようになる。図を見ると加速度および力は「中心より上にあると下向き、中心より下にあると上向き」となっている。これが「復元力」である。
波のグラフとしては、上に書いた$x$-$y$グラフの他に、時間を横軸にした$t$-$y$グラフがある。$x$-$y$グラフが「ある瞬間の波の形」を表したもの(いわばスナップショット)であるのに対し、$t$-$y$のグラフの方は「ある一点の場所での時間的変化の様子」を表したもの(いわば履歴)である。この2つのグラフについては後でまた述べよう。