前回の感想と復習
前回の感想・コメント
前回の授業に対する皆さんの感想・コメント(抜粋)が、
にあるので見ておいてください。
前回は波の基本と、干渉がどのように起こるかについてやりました。今回は波の起こすその他の現象について、続けて説明していきます。
縦波
前回うっかり入れ忘れたのでここで解説しておくが、波で「理解しにくい」と言われる現象の一つに「縦波」がある。まずはアニメーションを見てみよう。
アプリの説明ビデオが↓
アプリは↓。じっくりいろいろ試した後、ブラウザの「戻る」で戻ってくること。
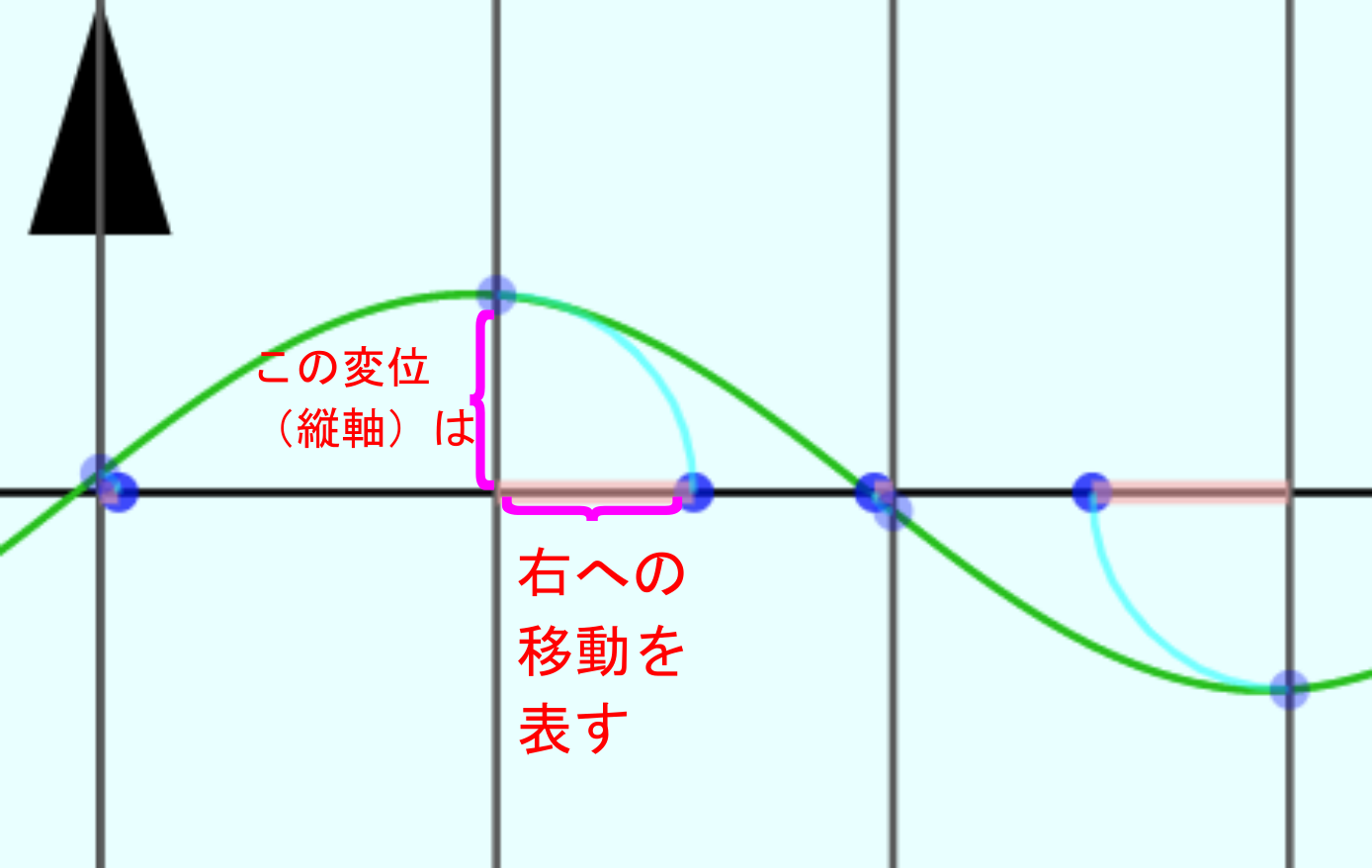
縦波はグラフの$y$軸にあたる上下が実は「前後の動き」を表現している。それはグラフの「上下(縦軸)」が実際には「左右(横軸)」の運動を表現しているからで、直感ではわかりにくいという生徒が多い。上のアプリでも出てくるのだが、↓のように「翻訳」をしながら見てあげなくてはいけない。
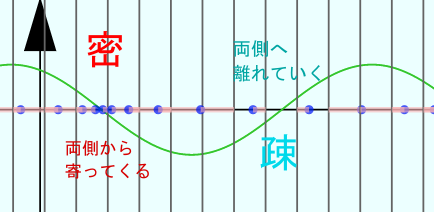
波(振動)は復元力があることで起こる という話を前回したが、縦波の場合の復元力は、「密度が高いところは密度が低くなるように、密度が低いところは密度が高くなるように」という「平坦化」の作用である。アプリの動きを見ながら、その作用がこの波を起こしているのだということを理解してほしい。
縦波の例は音だが、媒質である空気は「それぞれのつりあいの位置」の周りで振動しているだけで、「音の進行方向」に空気が移動しているのではない(←これもよくある間違いなので気をつけよう)。
波の反射と透過
波の反射の種類
進行した波が壁や、「違う媒質」に出会うと、そこで反射が起こる。
以下の説明はアプリを使って行う。アプリは↓のボタンをクリックすると使えるが、まずは説明を、という人は下のビデオとテキストを見たあとでアプリに進もう(アプリからは、ブラウザの「戻る」で戻ってくること)
アニメーションの中でも説明があるが、固定端反射と自由端反射はそれぞれ、以下のような特徴を持つ反射である。
固定端反射
反射点($x=0$)において合成波の変位が0になる(つまり、合成波が$x=0$の点では「固定」されている)場合の波の反射である。合成波は実際にこの場所で観測される波であり、入射波と反射波の重ねあわせでできている。
固定端反射の説明ビデオが↓
数式で表現すると
\begin{align}
入射波:&y_入= A \sin( kx-\omega t ) \\
反射波:&y_反= -A \sin( -kx-\omega t ) = A \sin( -kx-\omega t +\pi)
\end{align}
となる。ここで、kは波数で($2\pi \div$波長)、$\omega$は角振動数で($2\pi \div$周期)である。このような式になっていると、$x=0$において$y_入+y_反=0$になる。しばしば、「固定端反射では位相がπずれる」と表現されるが、それは$x=0$における波を、$y_入= A \sin( -\omega t )$と$y_反= A \sin( -\omega t +\pi)$のように表現することができるからである。
このように「位相がπずれる(変位が反転する)」理由は、固定端が「固定」されるためには入射波と反射波が境界部分できれいに足して0になっていなくてはいけないからである。
例によって、これもちゃんと理由があってそうなっていることなので「固定端ではπずれると覚えよう」なんて教え方をしてはいけない。
自由端反射
自由端反射とは固定端とは逆に、反射点($x=0$)が「自由に」動くことができる場合の波の反射である。自由という名前がついているが反射波が何でもよいという意味で自由なのではない。
自由端反射の説明ビデオが↓
数式で表現すると以下の通り。
\begin{align}
入射波:&y_入= A sin( kx-\omega t ) \\
反射波:&y_反= A sin( -kx-\omega t )
\end{align}
のように、今度は位相がずれない、という形で反射する。こうすることで、$x=0$において
\begin{align}
{\partial\over \partial x}\left(y_入+y_反\right)=0
\end{align}
という条件が満たされる。この条件の意味するところは$x=0$において合成波が平坦(傾き0)になれ ということである。アニメーションで実際そうなっていることを確認しよう。
屈折の違う媒質への入射
屈折率の違う媒質への入射
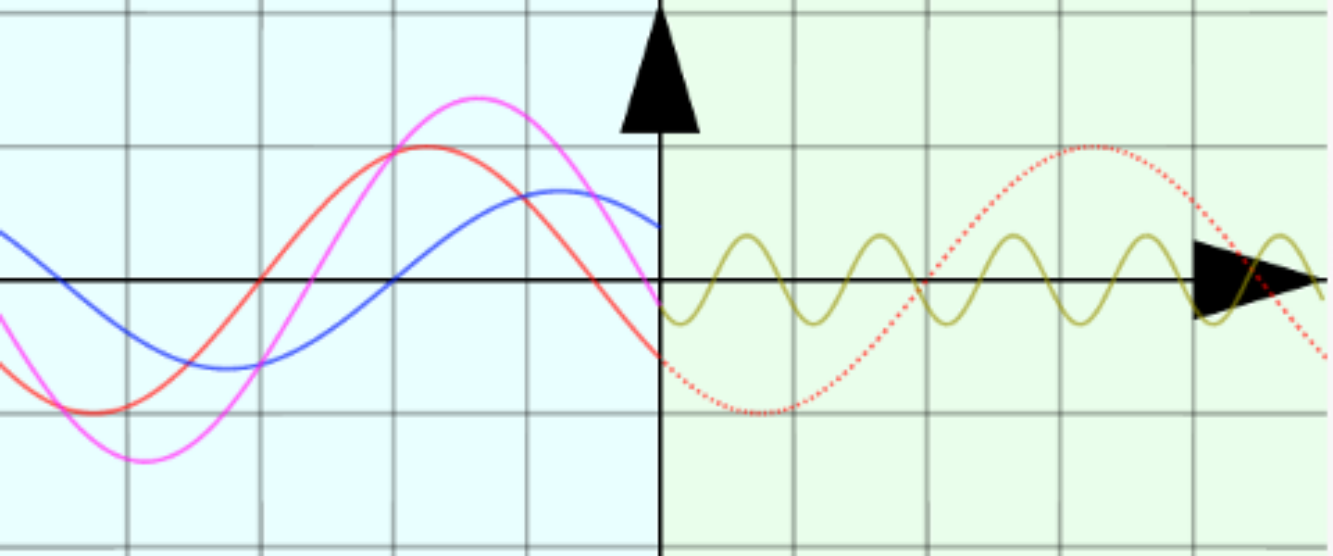
波が、「波長が変わってしまう境界」を超えて進むとき、そこで波が反射波と透過波に分かれるという現象が起こる。
説明ビデオが↓
\
アプリで「屈折率指定」とするとこの現象のアニメが見れる↓
アニメーョンで見せている波は、境界(x=0)で跳ね返されると同時に一部は内部にも進入し、透過波になる。透過波は元の波とは波長が変わっている。「屈折率」という数は、この波長の変化を説明する量である。$x>0$の領域と$x<0$の領域で(たとえばその場所での波の媒質が違うなどの理由で)波長(波数)が変化する場合がある。境界($x=0$)を超えることで波長が${1\over n}$になる場合(つまり、波数$k$が$n$倍になる場合)、「屈折率$=n$」と表現する。つまり
\begin{align}
屈折率 n={入射波の波長\over 透過波の波長}
\end{align}
である。
後で使うからついでに説明しておくと、このように境界を超えるとき、波の振動数は変わらない(変わってしまったら、境界部分の振動が「ずれる」)。なので、(振動数)×(波長)で計算できる「波の速さ」は波長に比例する。よって屈折率は
\begin{align}
屈折率 n={入射波の速さ\over 透過波の速さ}
\end{align}
となる。屈折率が2の場合、入射波の速さは透過波の速さの2倍(つまり、透過したときに速さが半分になる)。
↑このあたりの感覚も、アプリのアニメーションを見ながら実感しておいて欲しい。
たとえば「波長が半分になると速さが半分になる」なんてことは、屈折率を2にしてアニメーションを眺めていれば実感できると思うのだ。
ここで大事なことは入射波と透過波が境界$x=0$でつながっているだけではなく、その傾きもちゃんと接続されているということである。
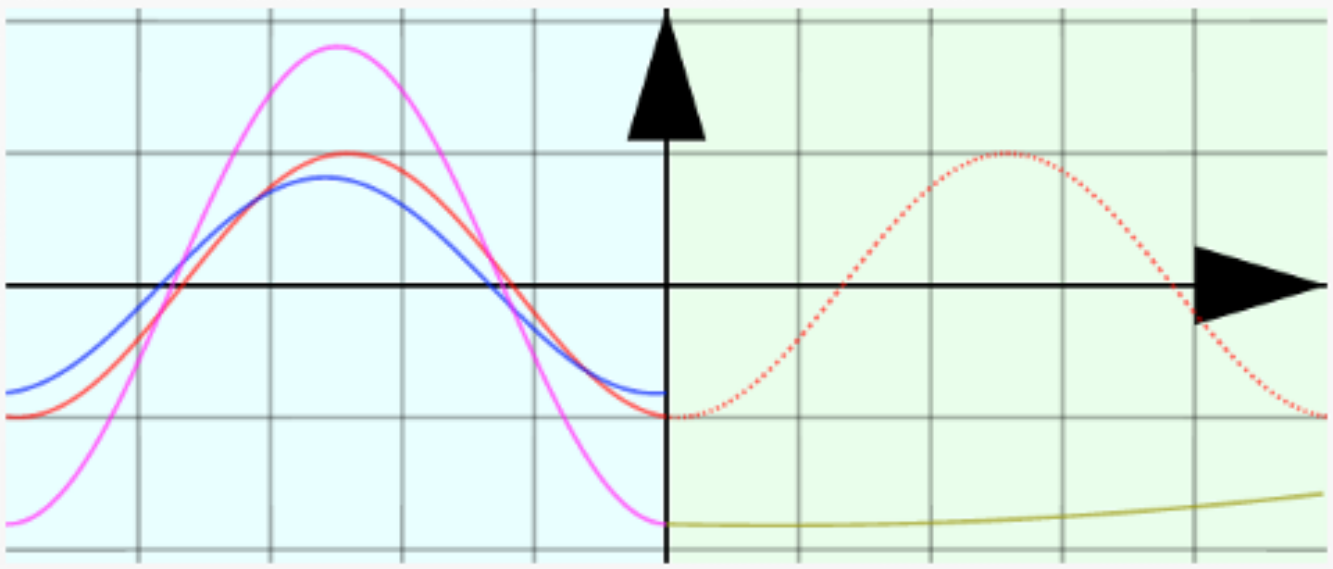
$n>1$のときの波の様子:
$n<1$のときの波の様子:
屈折率nが1より小さい時は「自由端」に近い形になっていることがわかるだろうか?---右側(透過後)では波長が長くなるのだから、左側(透過前)よりも平坦に近い波になり、これと接続されなくてはいけないから、自由端の場合に似た反射になるのである(屈折率$n$が大きい時はこの逆で、固定端に似た反射になる)。動くグラフをじっくり見て、この感覚をつかんで欲しい。
式で表現しておくと、屈折率$n$の場合の波の式は、
\begin{align}
入射波:&y_入= A\sin( kx-\omega t )\\
反射波:&y_反=A{1-n\over 1+n}\sin( -kx-\omega t )\\
透過波:&y_透=A{2\over 1+n}\sin( nkx-\omega t )
\end{align}
である。これが確かに、
\begin{align}
x=0~において、 ~~~
y_入+y_反=y_透,~~~
{\partial \over \partial x} (y_入+y_反)={\partial \over \partial x}y_透
\end{align}
を満たしていることは簡単に確認できる。
ここで反射波の係数に$1-n$が含まれているために屈折率$n$が1より大きいかどうかで反射波の位相が$\pi$ずれるかずれないかが決まる。
アプリは↓のボタンをクリック(ブラウザの「戻る」で戻ってくること)
屈折率が等しい場合の反射・透過
反射の話で、「屈折率が大きくなる媒質では固定端反射」「屈折率が大きくなる媒質では自端由反射」だという話をした。では
「屈折率が同じ媒質で起こる反射はどっちの反射?」
と聞かれたらどう答えるだろうか?
よ〜〜〜く考えてからここをクリック
「反射は起きない」というのが正解である。
なんなら、もう一度アプリ
をやって、屈折率を1にしてみよう。
あるいは、上の式で$n=1$にしてみよう。反射波が0になることがわかる。
波の屈折
下に波の屈折がとはなにかを説明するアプリがあるので、これを一通りやって、屈折現象のイメージをつかんでほしい。終わったらブラウザの「戻る」ボタンで帰ってくること。
アプリの説明ビデオが↓
アプリは以下のボタンをクリック(ブラウザの「戻る」ボタンで戻ってくること)
波長、屈折率、入射角、振動数をいろいろ変えることができるので、それをやりながら「なるほど屈折とはこういう現象なのか」ということをつかんで欲しい。本質は波長が変わる境界の上と下で波面がちゃんとつながる 、これだけに尽きるのである。
アプリの次のページとその次のページにあるのですでに見た人も多いと思うが、屈折はホイヘンスの原理からも説明できる。
↓上のアプリの2ページめ、ホイヘンスの原理を使って波がなぜ直進するかを説明する。
↓上のアプリの3ページめ、ホイヘンスの原理を使って波がなぜ直進するかを説明する。
屈折をホイヘンスの原理から説明する、アプリを使った説明ビデオが以下の通り。
ちゃんと数式でも出しておこう。
スネルの法則を出すところの説明ビデオ↓
「数式で」と言いつつ、本質的な部分は図形で説明している。図でイメージをつけていこう。
受講者の感想・コメント
青字 は受講者からの声、赤字 は前野よりの返答です。
主なもの、代表的なもののみについて記し、回答しています。
瓶詰めフィギュアの説明ビデオがとても興味深く感じた。
自分でも作ってみてください。100均の材料で作れます。
縦並みのグラフは横波のグラフと違い、変位がそのまま波形を表しているわけではないので、説明に工夫が必要だと感じた。 最後の屈折率のお話で、瓶にフィギュアを入れたもので例示していたが、安価で作りやすい機材のため説明に取り入れやすいと感じた。
縦波の説明はほんと、難儀します。
違う媒質を波が通る時、波長や速度が変わる理由を聞かれたときうまく答えられなかったので、ここで説明できるようにしたい
自分の言葉で説明できるよう、考えてみてください。
波を図で見るとわかりやすいなと思った。屈折率などをしっかり説明できるようにしていきたい。
図を使っての説明を、いろいろ考えてみてください。反射や屈折は透過後の波や媒質が変わった後にどう繋げるかを考えると、理解することが出来ました。
波はやはり、図での理解が大事ですね(まぁ物理みんなそうなんですが)。
屈折率の違いによって物体が見えたり見えなかったりする現象を利用して物を隠す話が某推理系漫画で出てきた覚えがあります。 自分が復習していた範囲がちょうどトリックに使われていて『分かる!何を言っているのかが想像つくぞ!』と思って印象に残っています。 自分の勉強した内容が目の前の現象を説明するのに使われていると記憶に残りやすいのではないかと思いました。
フィクションの話でも、授業の中に取り入れていくと楽しいかもしれませんね。