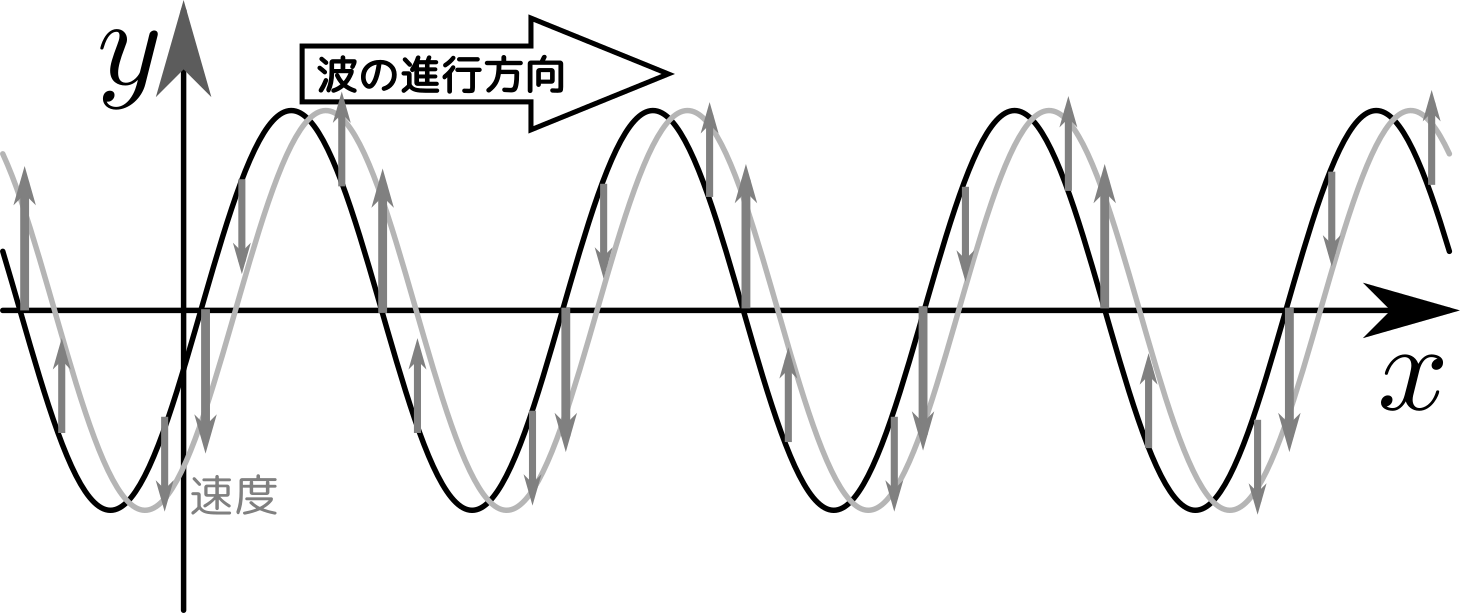
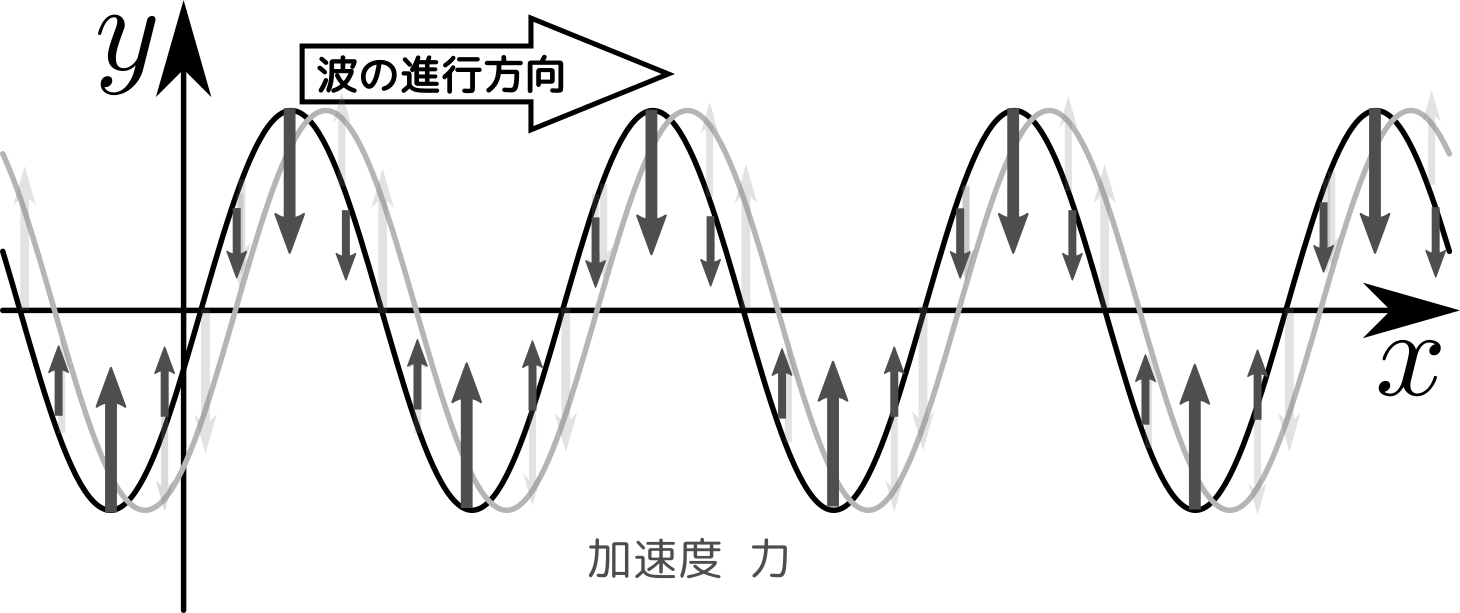
位相
$\sin A$の$A$の部分を「位相」と呼ぶ。
「位相」という言葉も嫌われるのだが、要は「三角関数の引数」のことなので、「角度」と同じようなものだ。ただ、上の図に書いたような「架空の円運動の角度」なので「角度」とは別の言葉を当てている。
下に位相とはなにかを説明するアプリがあるので、「位相」という言葉のイメージをつかんでほしい。終わったらブラウザの「戻る」ボタンで帰ってくること。
アプリの説明ビデオが↓
アプリは以下のボタンをクリック(ブラウザの「戻る」ボタンで戻ってくること)
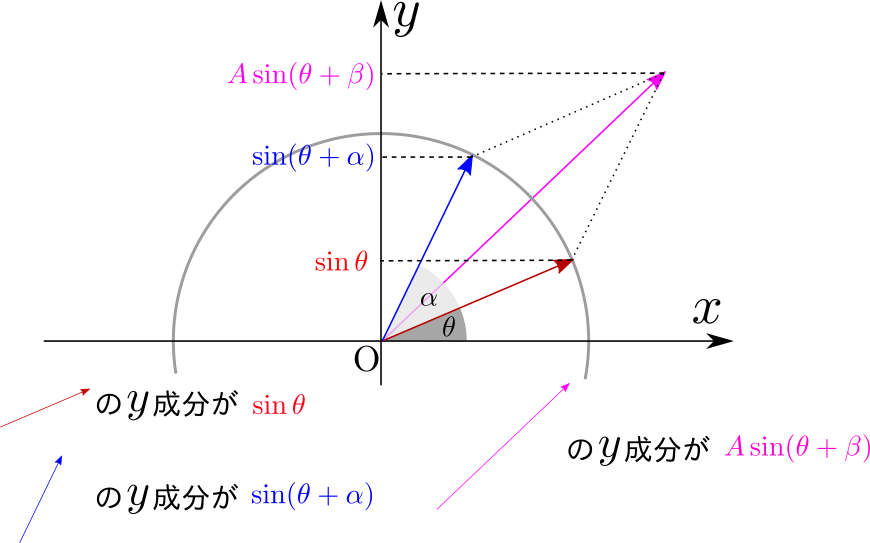
たとえば
$$\sin\left(A+{\pi\over 2}\right)=\cos A$$
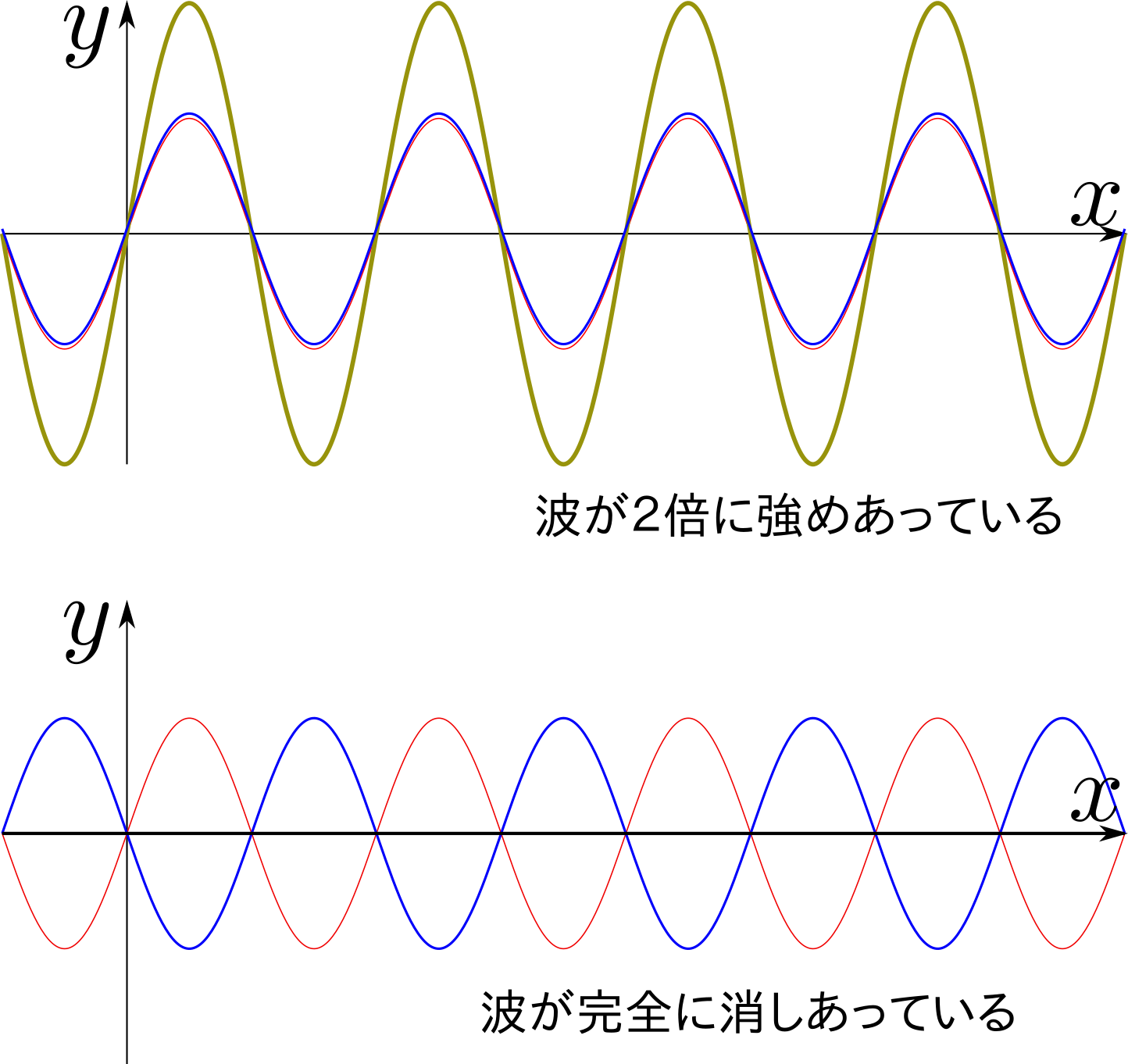
という関係(他にもいろいろある。下のような図を描くと確認できる)があるので、「位相に${\pi\over 2}$を足せば$\sin$と$\cos$は入れ替わる」ということが言える。
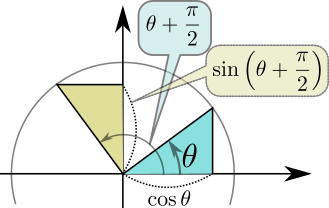
$\sin$と$\cos$は平行移動を除いて同じ関数だと思っていいので、以下は$\sin$だけで話をしよう。
波の変位の式
以下の計算の説明ビデオ↓
波長が $\lambda$ の波が $x$軸上に進行しているとき、ある瞬間( $t=0$とする)の波の変位の式を
\begin{align}
y=&A\sin\left(
{2\pi x\over \lambda}+\alpha\right)
\end{align}
と書くことができる。これを「公式だ〜」と暗記しようとしてはいけない。こういう式が出てくる背景も含めて考えておかないといけない。
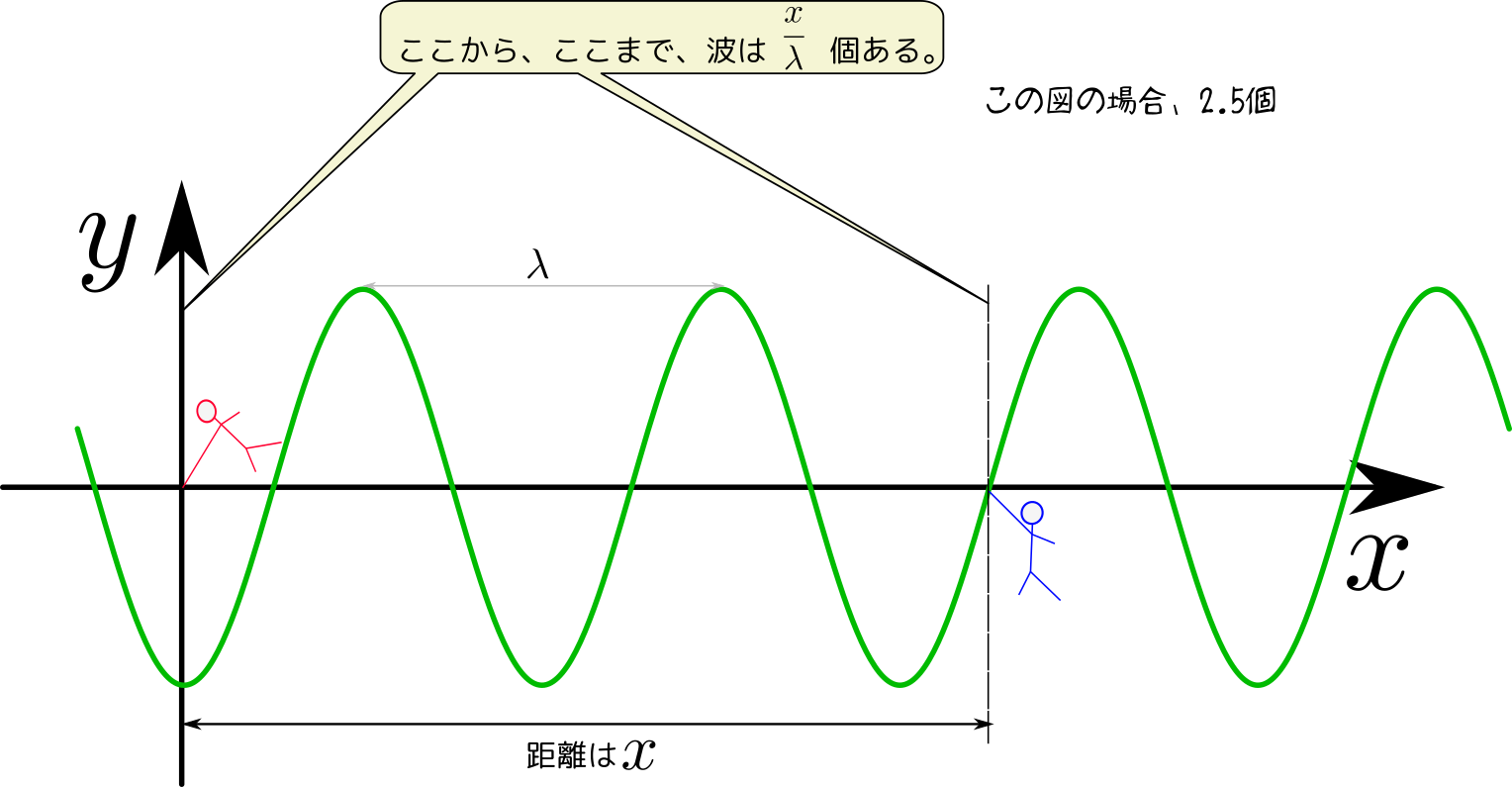
$\lambda$ は「波一個の長さ」である。 $x$ は「原点からの距離」だから、 ${x\over\lambda}$は「原点からここまでに入っている波の数」を表現している。
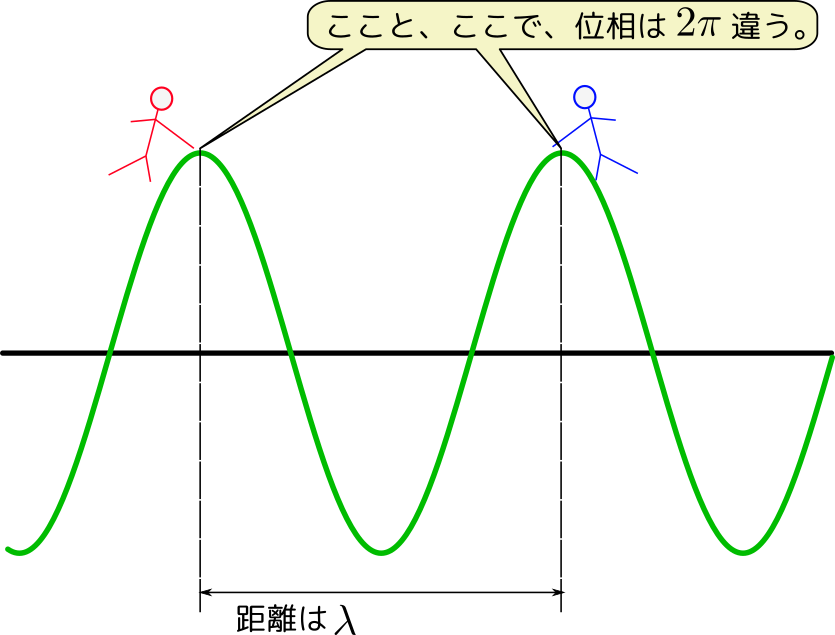
位相の中の${x\over \lambda}$に$2\pi$が掛かる理由は「波1個で位相変化$2\pi$」という関係があるからである。
今考えている状況では、「$x$が$\lambda$増加すると、$\sin$の位相が$2\pi$増える」という関係になっているので、それを表現する式もそれを反映した形になっている。
ここで描いたグラフ、および使った式$y=A\sin \left({2\pi x\over \lambda}+\alpha\right)$は、「ある瞬間の波を表現する式」であって、波の時間的変化は表現できていない。そこで
時刻$t=0$では$y=A\sin \left({2\pi x\over \lambda}+\alpha\right)$が成り立っていたとして、任意の時刻ではどんな式が成立するのか?
という問題を考えてみよう。
今度は時間の経過による位相変化だが、ここでも「波1個は位相変化$2\pi$」という関係がある。時間$t$が周期$T$だけ経過すると、${t\over T}$個の波が出るから、${2\pi t\over T}$だけ位相が減少する。
ここで「なぜ減少する?」と疑問が湧く人は、もう一度アプリを見直してみよう。
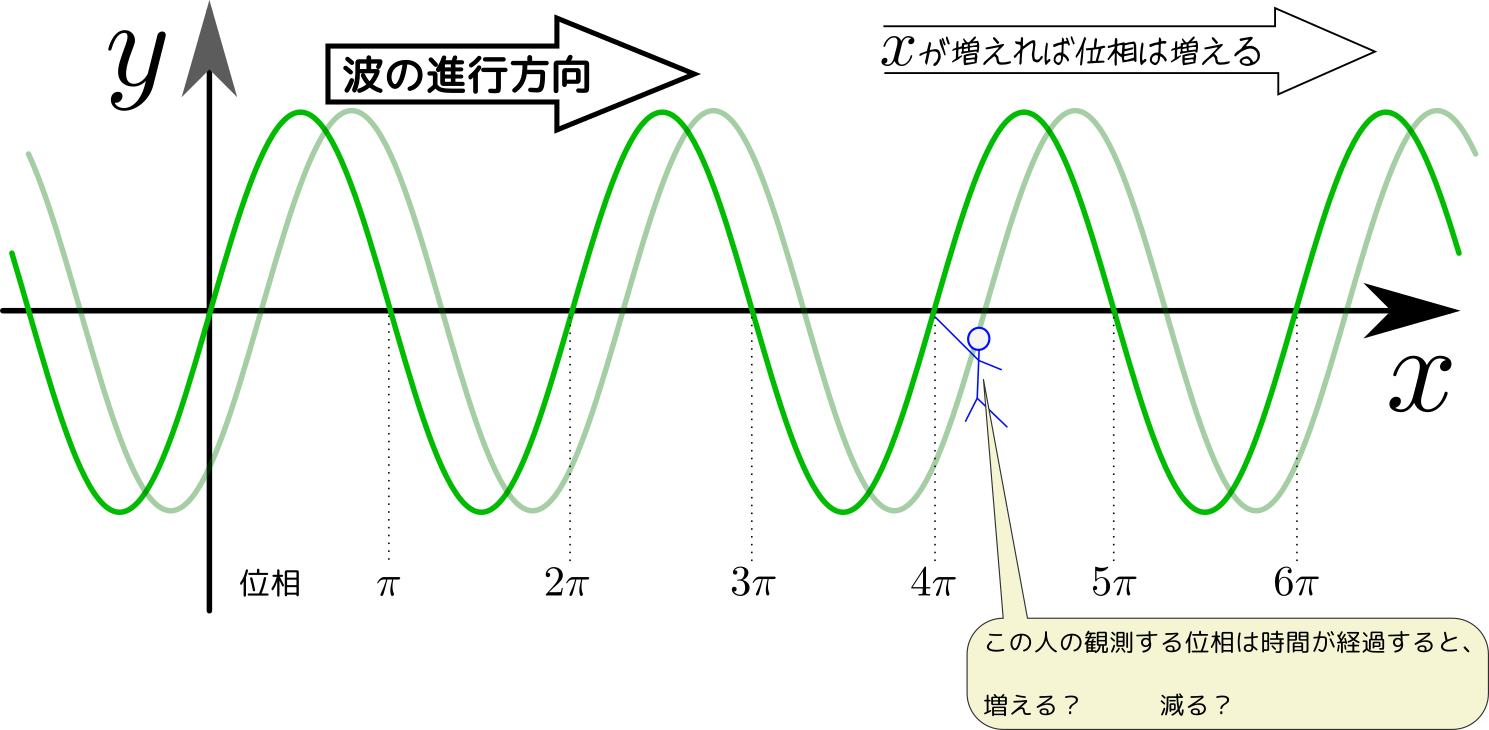
よって式は
\begin{align}
y=A \sin\left(2\pi\left({x\over \lambda}-{t\over T}\right)+\alpha\right)\label{naminosiki}
\end{align}
となる。
ここでもう一度強調しておくと、こういうのを「公式だから覚えよう」と思ってはいけない(自分で勉強するときもそうだが、特に教えるときにそんな教え方をしてはいけない)。式それぞれに意味があるのだから、その意味を考えて(できれば今やったように自分で導出して)「なるほどこういう方法で導くのか」を納得しよう。教える立場にいるものが、それができないようでは、教えるときに説得力がない。
波の進行方向が逆($x$軸の負の向き)であるときは、位相は時間が経つと増加するので、$ y=A \sin\left(2\pi\left({x\over \lambda}+{t\over T}\right)+\alpha\right)$になる。
この式は
\begin{align}
y=A \sin\left(2\pi\left({x-{\lambda\over T}t\over \lambda}\right)+\alpha\right)
\end{align}
と書き直すことができる。 ${\lambda\over T}$が波の伝搬速度(もちろんこれもなぜこうなるのかを納得しなくてはいけない。意味を考えれば納得できる式なのだから!)だから、
\begin{align}
y=A \sin\left(2\pi\left({x-vt\over \lambda}\right)+\alpha\right)\label{naminosikivt}
\end{align}
と書くことができる。
この式は、
関数$y=f(x)$を$x$方向に$a$だけ平行移動すると $y=f(x−a)$になる。
という数学の知識を思い出せば、
$y=A\sin\left({2\pi x\over\lambda}+\alpha\right)$を $x$ 方向に $vt$だけ平行移動した式が、
\begin{equation}
y=A\sin\left({2\pi(x-vt)\over \lambda}+\alpha\right)
\end{equation}である。
と考えて出すこともできる(いろんなやり方を理解して、将来教えるときに使えるようにしよう)。
下の図のように考えても同じ式が出せる。考えてみよう。
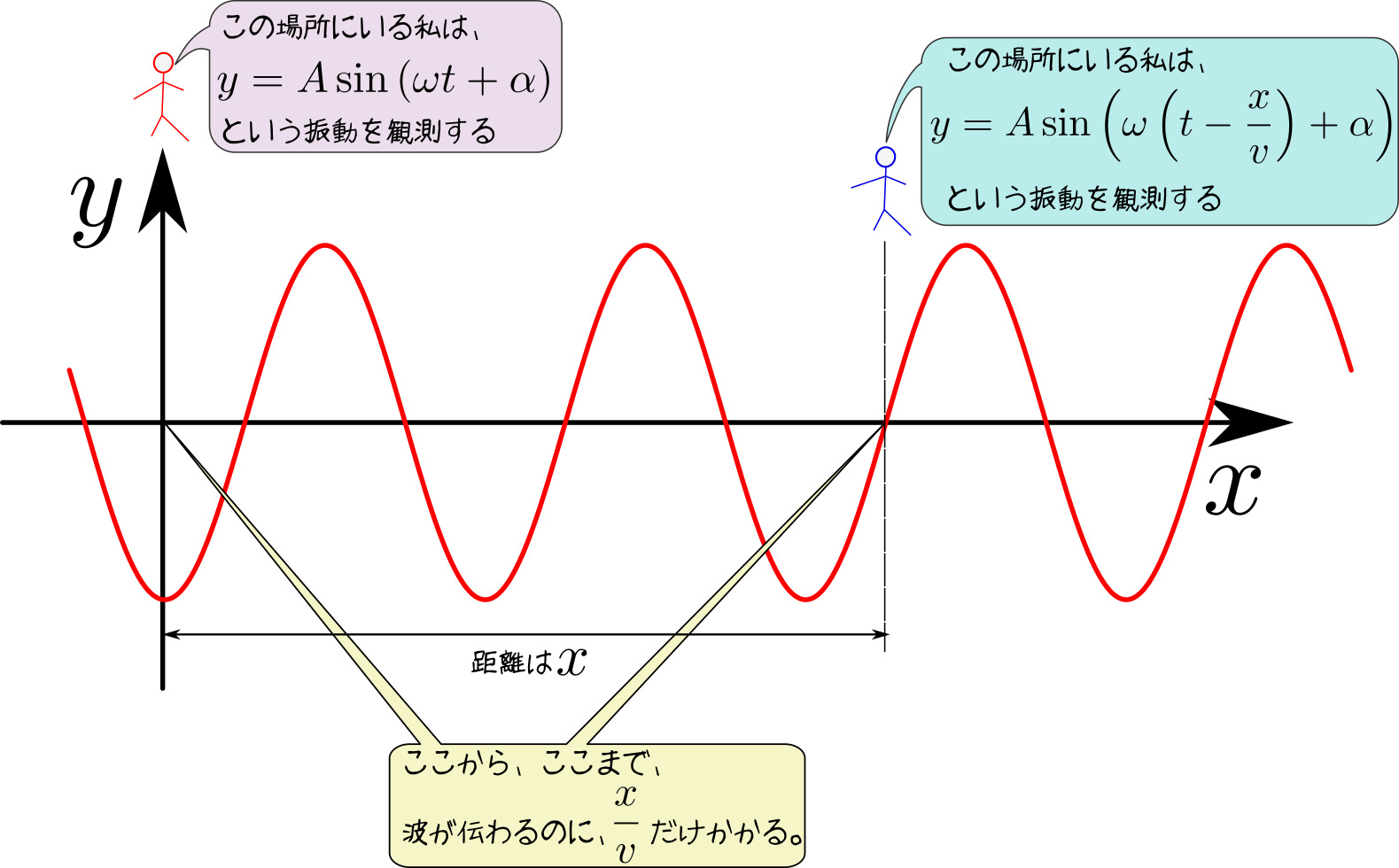
くどいようだが、一つの式を出すにもいろんな考え方から出せるようにしておく。そうすると教え方にも幅が出る(教わる生徒の方も、ある方法ではわかりにくいが別の方法で説明されるとさっとわかったりする)。
$\omega={2\pi \over T}$と代入してやると上の図から作られる式はほぼ上の式と同じになる。実は符号が逆になっているが、それは位相が$\pi$ずれているだけのことなので本質的に違いはない。