保存則の出し方
運動量保存則
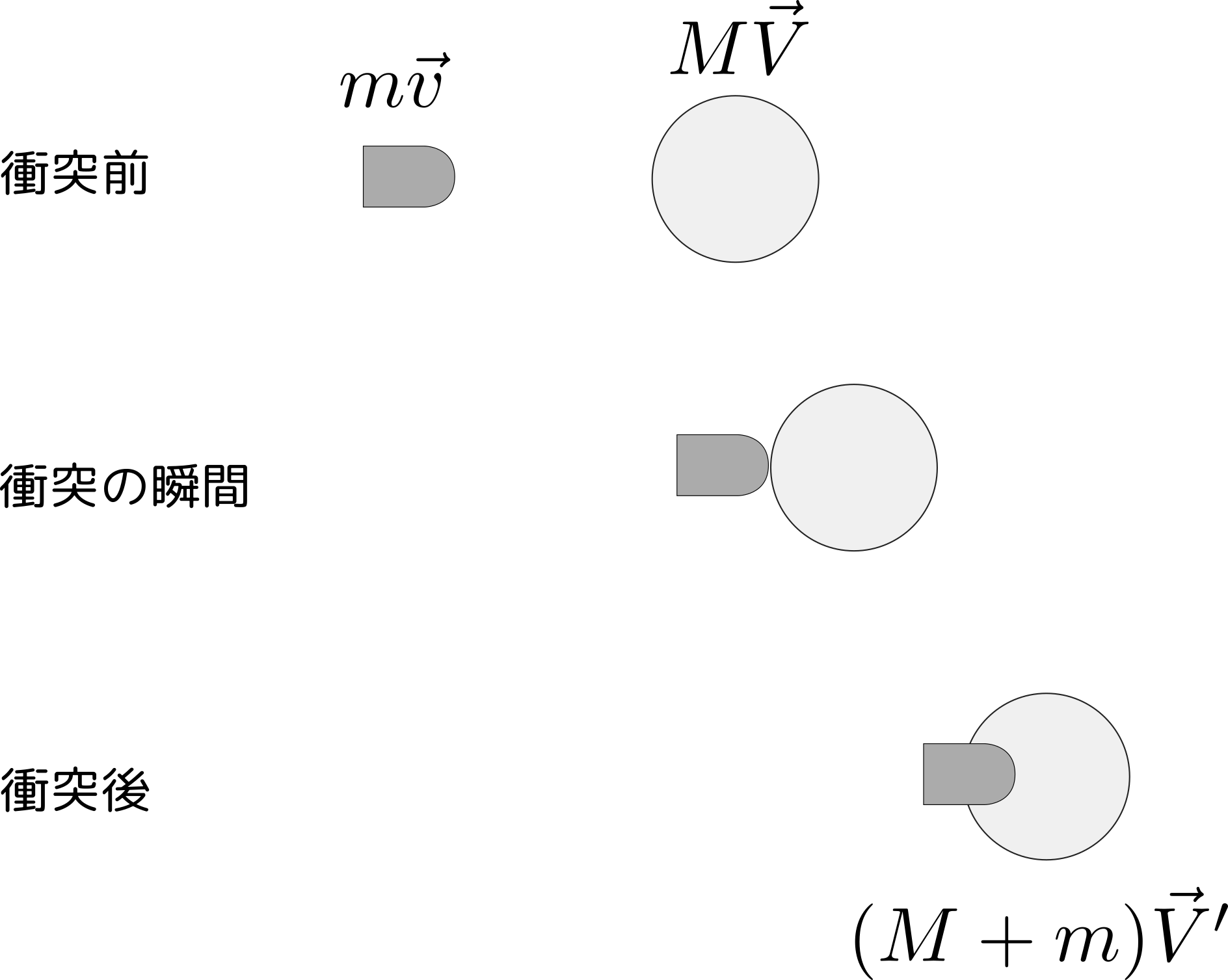
二つの物体が
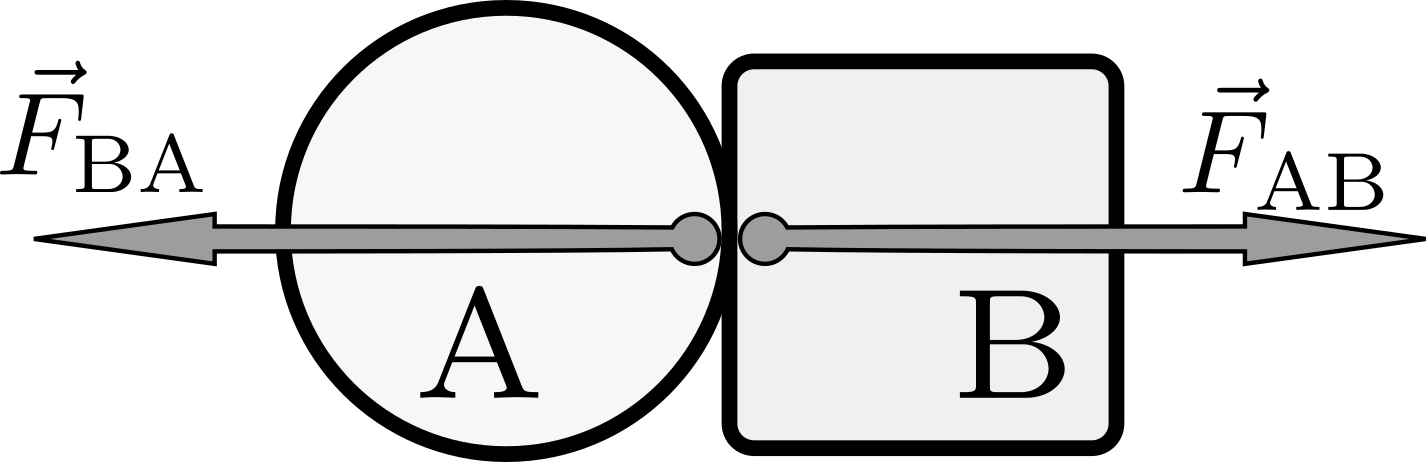
のように力を及ぼし合っているとする。
作用反作用の法則$\vec F_{\rm AB}+\vec F_{\rm BA}=0$から、運動方程式$\vec F=m{\mathrm d \vec v\over \mathrm d t}$を用いて $$ m_{\rm A}{\mathrm d\vec v_{\rm A}\over \mathrm d t} + m_{\rm B}{\mathrm d\vec v_{\rm B}\over \mathrm d t}=0 $$ が言える。これは $$ {\mathrm d \over \mathrm d t}\left(m_{\rm A}\vec v_{\rm A}+ m_{\rm B}\vec v_{\rm B}\right)=0 $$ と書き換えることができて、運動量保存則そのものである。
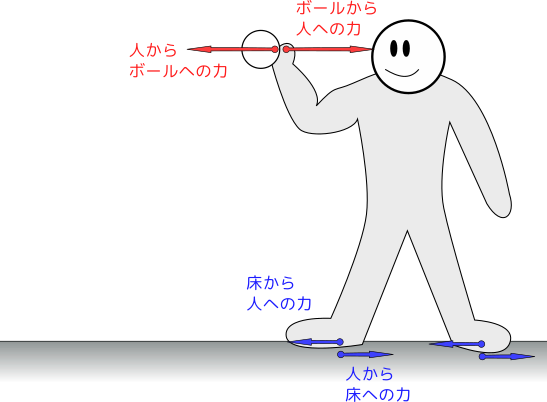
次にエネルギーの方を考えよう。同様に二つの物体それぞれに働く力を$\vec F_{\rm AB}$と$\vec F_{\rm BA}$とする。この二つの物体が
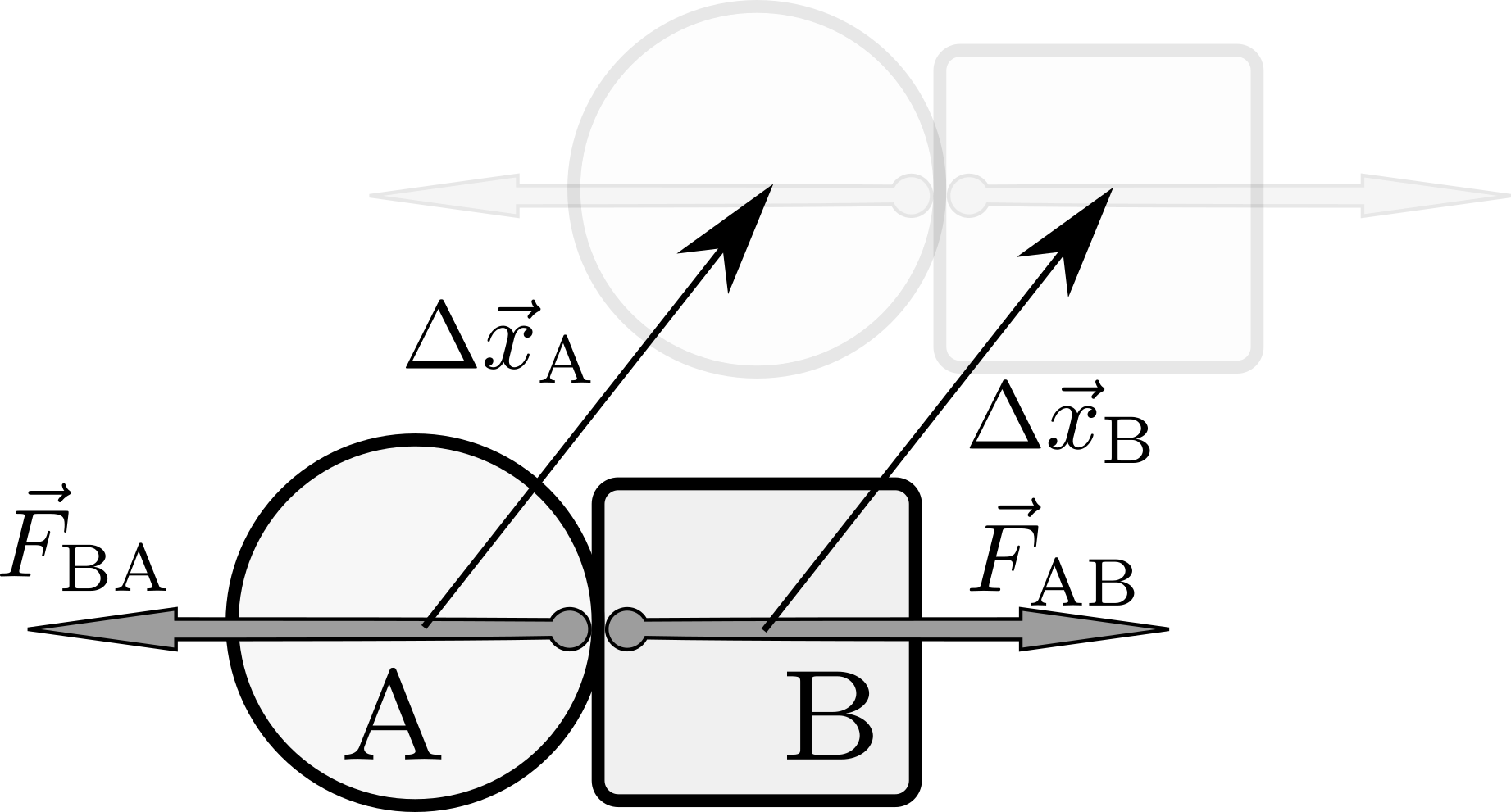
のように同じ動きをしたとしよう($\Delta \vec x_{\rm A}=\Delta \vec x_{\rm B}$に注意)。
この図の状況であれば、$\underbrace{\vec F_{\rm AB}\cdot \Delta \vec x_{\rm B}}_{系{\rm A}が\atop 系{\rm B}にした仕事}$は正で、$\underbrace{\vec F_{\rm BA}\cdot \Delta \vec x_{\rm A}}_{系{\rm B}が\atop 系{\rm A}にした仕事}$は負である(絶対値が等しい)。すなわち $$ \vec F_{\rm AB}\cdot \Delta \vec x_{\rm B}+\vec F_{\rm BA}\cdot \Delta \vec x_{\rm A}=0 $$ が成り立つ。「Aにされた仕事」と「Bにされた仕事」の和は0となり、全エネルギーは保存する。
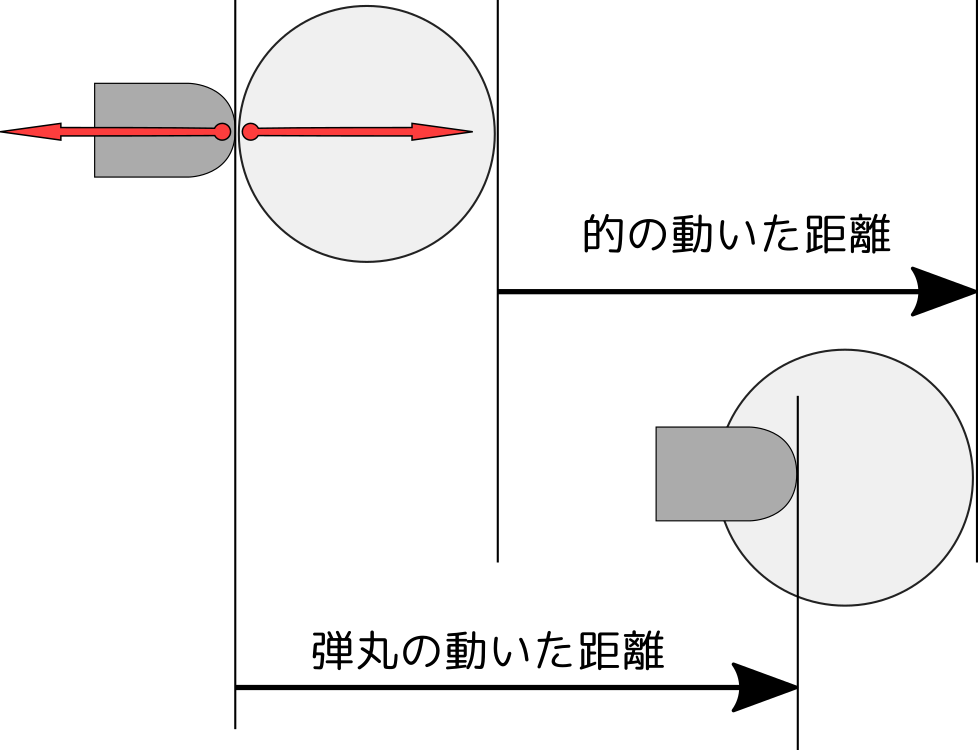
しかし、物体に変形が生じるなどの理由で
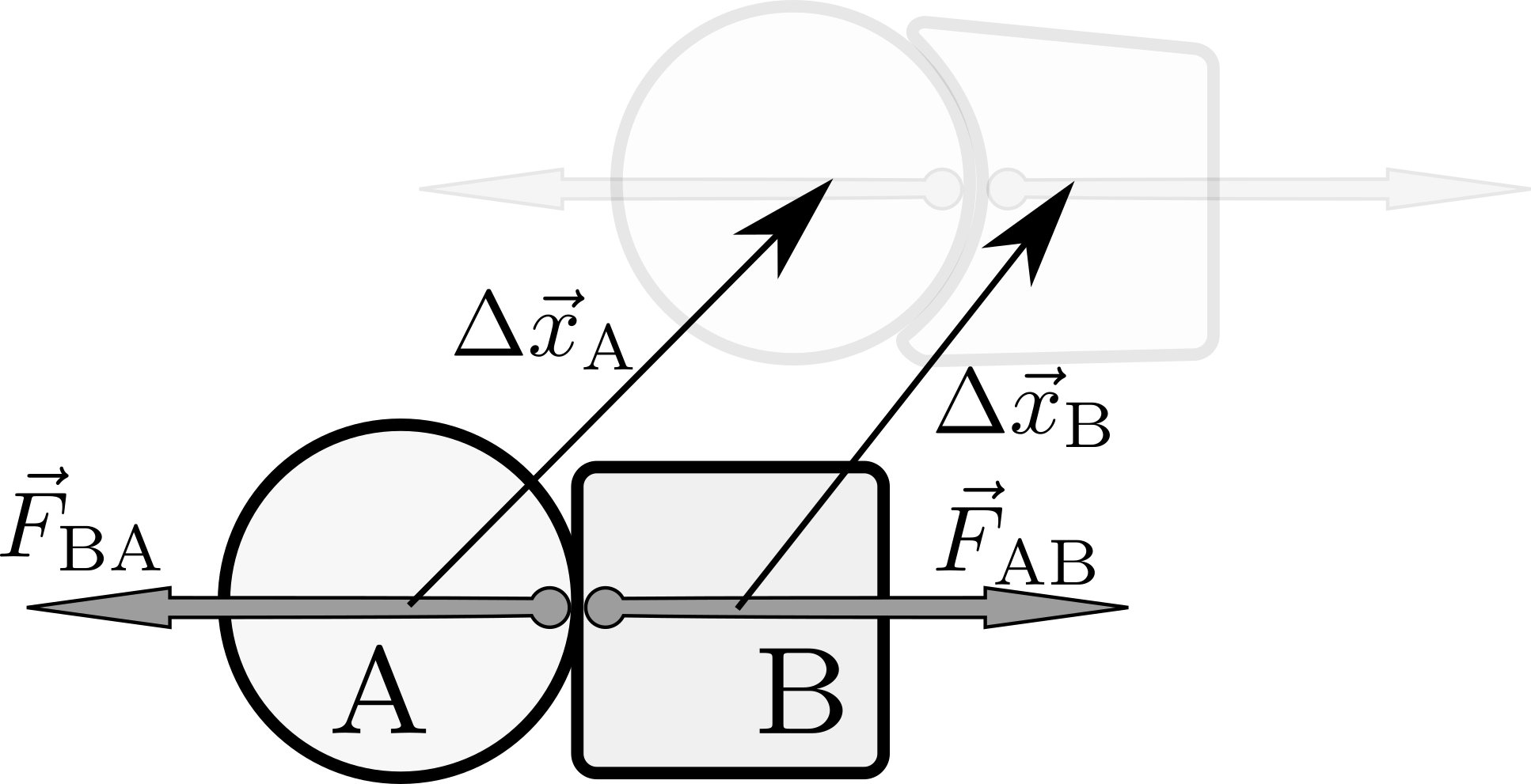
のようになって二つの$\Delta\vec x$が一致しないならば、 $$ \underbrace{\vec F_{\rm AB}\cdot \Delta \vec x_{\rm B}}_{系{\rm A}が\atop 系{\rm B}にした仕事}+ \underbrace{\vec F_{\rm BA}\cdot \Delta \vec x_{\rm A}}_{系{\rm B}が\atop 系{\rm A}にした仕事}\neq0 $$ となることも起こり得る。図の状況で左辺の$\underbrace{\vec F_{\rm AB}\cdot \Delta \vec x_{\rm B}}_{系{\rm A}が\atop 系{\rm B}にした仕事}$は正で、右辺にある$\underbrace{\vec F_{\rm BA}\cdot \Delta \vec x_{\rm A}}_{系{\rm B}が\atop 系{\rm A}にした仕事}$は負であることに変わりないが、絶対値は後者の方が大きい。よってこの場合、「Aにされた仕事」と「Bにされた仕事」の和は負になる(エネルギーが失われる)ことになる。この失われたエネルギーは「物体の変形に使われた」と解釈される。
変形などが起こってエネルギーが保存しないように見えるときも、物体の持つ内部エネルギーを考慮に入れて考えると全エネルギーは保存する。
以上からわかることは、外力(系内の物体以外から及ぼされる力)が仕事をしないで、かつ内力(系内の物体同士の及ぼし合う力)のする仕事が消し合う(消し合うのは「力」ではなく「仕事」であることに注意)なら、その系のエネルギーが保存するということである。