第１章 量子力学の「あらすじ」-光の粒子性を中心に
この章では、これから「初等量子力学」および「量子力学」で学ぶ量子力学のあらましをつかんでもらうために、まず光の粒子性ということについて概観を述べる。詳細な計算などは後で述べるが、まずは量子力学とはどのような学問なのかの「あらすじ」を知ってもらいたい。
1.1 光は波か粒子か
19
世紀頃、「物理はもうすぐ終わる」と言われていた。力学、電磁気学がほぼ完成し、天体の運動がニュートン力学で完全に予言されるようになった。ところが次
の年から20世紀だという1900年、プランクは黒体輻射に関する研究から「光のエネルギーは不連続な値を取る」という仮説を発表した(このプランク
の主張までは、光に限らずエネルギーというのはいかなる値でも取ることができると思われていた)。これが量子力学の始まりである。量子力学と直接関係はな
いが、20世紀の始まりには特殊相対性理論1も作られている。量子力学と相対論が、「終わる」はずだった物理の世界を一変させてしまったのである。
せっかくなので、ここで「今年は世界物理年で、なぜかというとちょうど100年前にアインシュタインが相対性理論と光電効果とブラウン運動についての三大論文を出したんだよ」という話をした。
光は波であるか粒子であるか、というのはニュートンやホイヘンスの時代(17世紀後半)でも論争になった謎であった。ニュートンは光が直進するというこ
とから光は粒子であると考えた。波ならば広がるはずであり、「光線」という言葉で呼ばれるような形状にはならないと考えたのである。
しかし、後に光が干渉現象を起こすということが明らかになったので、「光は波である」と
20世紀初頭までは考えられた。また、マックスウェルが電磁気学の方程式から光速で進む波動解(電磁波)を見つけたことも光が波であることを支持してい
た。つまり、光とは空間中の電場と磁場が振動して、それが伝わっていくものなのである。
このようにして19世紀までは「光は波である」ということで決着がついたと思われていた。ところが1900年、プランクが以下のようなことを主張する2。
振動数nを持った光のエネルギーは、hnの整数倍に制限される(hはプランク 定数で、SI単位系での値は6.6×10-34J·sec)。
プランク以外にもいろんな研究により、光は一個あたり(プランク定数)×(振動数)というエネルギーを持った粒子(「光子」と名付ける)でできていると
わかった(なぜこんなことがわかったのか、という点は、次の章でくわしく説明する)。プランク定数は非常に小さいゆえに、通常我々が目にする光は、たくさ
んの光子の集まりでできている。
光のエネルギーが不連続だと言われてもにわかに納得しがたいと思うが、同様に連続に見えて実は連続でない例として、コップの水を考えよう。コップの水は連続的で、切っても切ってもいくらでも小さくなるように見える。けど、実際には水はH2O分子でできているのだから、切っていってH2O
一個になったら、もう切れない。同じように、光を切っていったとすると、これ以上切れない単位がある。たとえば向こうから光がやってくる時に、一瞬だけ
シャッター開けてすぐ閉める。シャッター速度を短くすればいくらでも小さいエネルギーの光を切り取れそうだけど、そうはいかない。hnの整数倍というエネルギーの光しか作れないのである。
【捕捉】この部分は授業では話さない可能性もあるが、その場合は読んでおいてください。
ニュートンは直進することを光が粒子である理由としていた。では、光は波であるのに、なぜ直
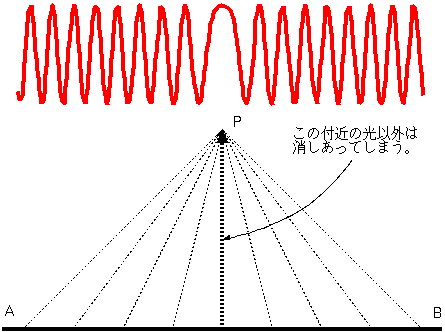
進する(ように見える)のだろうか。波動説にしたがえば、光はいろんな方向に広がろうとするはずである。右の図のように、ある直線ABの上から出発した波
が、ある一点Pにやってくるところを考えよう。直線AB上では波の位相はそろっている（山なら全部山、谷なら全部谷）が、そこから離れた点にやってきた
時、線上から点Pまでの距離の違いから、やってくる波の位相にずれが生じている（あるところからきた光は山、別のところからきた光は谷）。図の上の方に書
いてある波形は、AB上からP点にやってきた波がどのような状態でやってくるかを書いたものである。
波は干渉するので、山と谷がぶつかると互いに消しあう。上のグラフのようになっていると、真
ん中付近をのぞいてはほとんどすべての波が消しあって消えてしまう。真ん中付近は位相（つまり距離）の変化が比較的緩やかなので足し算しても消されずに残
る。特に波長が短いと、この振動がより激しくなり、消しあう可能性がより高くなる。結局、中央付近のあまり消しあわない波だけが、現実にこの場所にやって
くる波だということになる。
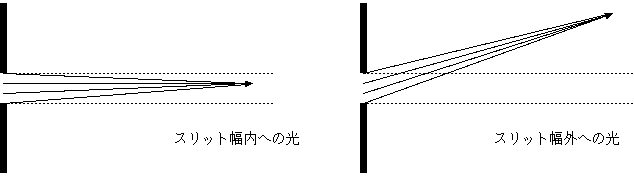
単スリットを通り抜けた後の光を考えよう。右側にやってくる光はスリットを通り抜けた光の和であるが、スリットの幅よ
り外にやってくる光は、上で説明した、位相の変化の少ない部分を含まないので、互いに消しあってしまう。スリット幅より内側については光がある程度消され
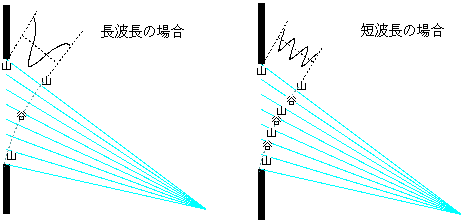
ずに残る。実際に計算してみると、波長が短い時には図の点線より外側での光の振幅はほとんど０になってしまうことが確認できる。
波長が長いかスリットの幅が非常に小さいかどちらかの場合は、やってくる光の位相変化が小さいので、波は広い範囲で消されずに残る。
図は波長が長い場合と短い場合で、単スリットを通り抜けた光がどのように重なるかを描いたものである。短波長の場合、図に示した点にやってくる光はたくさんの山と谷が集まってできたものとなり、必然的に小さな振幅になってしまう。
長波長の場合には、光は波として広がることになる。光学の方では「波長とスリット幅が同程度の時よく回折が起こる」と言われるが、それはこういう理由である。
このような単スリットの回折の波の様子を見せるjavaアプレットがあるので、見たい人はこちらへ。
つまり、各点各点の波としての光は広がろうとするのだが、光全体の進む路から離れたところへ来た波は互いに消しあってしまうので、全体としての光は広がることができないのである。厳密に言うと、少し広がっているのだが、その広がりが小さくて見えない3。これは、後で出てくる「波動関数(これが何なのかはまだわからなくてよい)で表される粒子が、なぜ直進するのか」という疑問に対する答でもある。覚えておこう。
【捕捉終わり】
↑の捕捉はしゃべらないつもりだったが、ヤングの実験の話をしていたら「なぜ光は直進したり広
がったりするのか」という意味の質問が出たので、結局javaアプレットを見せながら話した。波長とスリット幅によって、広がりを見せたり直進性を見せた
りするのが波の面白いところだが、その性質は量子力学でも不確定性関係という形で顕れてくる。早い時期にこの話ができたのはよかった。
実は光の粒子性は特殊な現象を見なくても、日常生活にも現れる。たとえば夏に太陽の光を浴び
ると日焼けするが、冬に電気ストーブにあたっても日焼けすることはない。得られるエネルギーは同程度であっても、紫外線と赤外線では質が違う。古典的に見
るとそれは振動数の違いであり、「紫外線の方が振動数が大きい(振動が速い)から、人間の体に化学変化を起こさせるのだ」という考えもできないではない
が、現実にはうまく行かない。光を光子の集まりとして考え、赤外線(振動数が小さい)は一個一個のエネルギーが低い光子でできており、紫外線は一個一個の
エネルギーが高い光子でできていると考えられた方が実験に合う。人間の体に化学変化を起こさせるのは、この光子一個一個の衝突だと考えるとこの現象が理解
できる4 (演習問題1-1を参照せよ)。
例えば、夜空の星を見上げればすぐに星が見えるが、これも光が光子という塊で降ってくるおかげである。眼が見える(人間が光を感知できる)のは、眼の中に
ある化学物質が光に反応して化学変化を起こすからである。しかし、光が連続的にやってきて、エネルギーがたまって始めて反応が起こるのだとすると、長い時
間がたたないと感知できないことになる(演習問題1-4を参照せよ)。
光って大きさあるんですか？（黒板に光の粒が飛んでいる様子を ○→ のように書くので、どうしてもこんな質問が出る）
ありません。図はあくまで絵です。
絵と言えば、光ってたいてい〜〜〜〜って感じで波線で書くもんだから、ほんとにあんな線を描いて進んでいるんだと思いこんでいた人がいました。ある日私の部屋に来て
「光は秒速３０万キロで進むっていうけど、蛇行して進むんだから３０万キロより遅くなりますよね！」
と大発見したような顔して言ってました。でもほんとは光はちゃんと直進します。
という話をしたら、最後に書いてもらった感想の中に「ぼくもそうでした」というのがあった(^_^;)。
重さもないんですか？
相対論の方で「質量」というのをどう定義するのかを勉強するけど、その定義では質量はありません。でも忘れないでほしいのは「ぶつかることによって何かを動かすことはできる」ということ（そういう意味での“重さ”はある）です。
1.2 二重スリットと波束の収縮
光が波でありながら粒子である、ということは非常に理解しがたいことであろう。しかし今は「あらすじ」の段階なので、これをどう理解すべきかということはとりあえず後に回す。ここではさらに別の例で光の粒子性がどのような現象を起こすのか、を見ていく。
そこで、光の波動性を表す実験として有名なヤングの実験を考えよう。ヤングの実験では点光源(実際の実験では単スリットで点光源化することが多い)から出た光が、複スリットを通った後回折5してスクリーンにあたり、そこに干渉縞が生じる。
二つのスリットからスクリーン上にやってきた光の電場をE0sin(k(r1-ct))およびE0sin(k(r2-ct))としよう。電場の振幅E0は定数ではなくrが大きくなるほど小さくなるはずであるが、ここでは簡単のために定数とおいた。スクリーン上にできる電場はこの二つの和なので、
|
E0(sin(k(r1-ct))+sin(k(r2-ct))) |
| (1.1) |
とおける。xが変化すればそれに応じてr1,r2も変化していく。二つの項sin(k(r1-ct))とsin(k(r2-ct))もそれに応じて振動していくが、うまく両方の位相がそろったところは強めあって振幅の大きい電場となり、位相が反対になっていると弱めあって振幅が０になる。この和を具体的に計算すると、公式sinA+sinB = 2cos([(A-B)/2])sin([(A+B)/2])を使って、以下のように書ける。
|
2E0cos |
(
|
k
2
|
(r1-r2) | )
|
sin |
(
|
k
2
|
(r1+r2)-kct | )
|
|
| (1.2) |
この式から、cos(k/2(r1-r2))=0となる点には光がこないことがわかる。
|
|
[問い1-1]
この二つの光の光路差r1-r2を計算し、スクリーン上で暗くなる場所のx座標を求めよ。ただし、光の波長をlとし、Lはdおよびlに比べて十分大きいとして近似せよ。必要ならば公式(1+x)n @ 1+nx(x << 1の時)を使え。
[問い1-2]
二つのスリットから出る電場の和から、スクリーン上の電場のエネルギー密度1/2eE2の一周期分での平均を計算せよ。
ヒント：sinq,cosqなどは一周期分積分したら0になる。
sin2q = [(1-cos2q)/2]となるが、cos2q
の部分もやはり、一周期分積分すると0である。
|
|
↑この問題は今日の宿題です。
ヤングの実験をアニメーションで見るjavaアプレットはこちら。
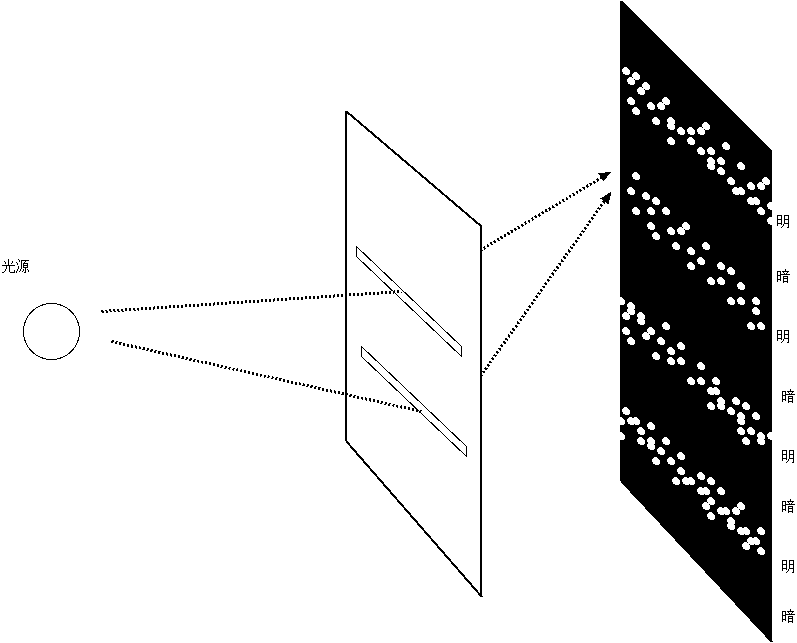
この実験を、「光は粒子でもある」という知見のもとに考え直すと、いろいろ不思議なこ
とが出てくる。上の図はこの実験の様子を、光が粒子であるという観点を強調して描いたものである。粒子説にしたがえば、光がやってくるということは実際に
は光子がやってくるということである。つまり、ヤングの実験で発生する明暗の縞は、実は左の図のように、光子の当たる場所と当たらない場所が発生している
ということになる。
と、だいたいこのあたりで今日は時間切れ。来週は二章からなので、以下は話さないが、以下と同様の話はいずれ話すことになるだろう。
以上の実験からわかることは、あたかも「一つの光子が二つのスリットを同時に通ってきた」と
解釈できるような現象が起こっているということである。つまりこのスクリーンにあたった一個の光子は「上のスリットを通ってきた光子」でも「下のスリット
を通ってきた光子」でもなく、いわばその重ね合わせとして存在しているのである。
たとえば上のスリットをふさいだとする。すると、光子は「暗」の場所にも当たるようにな
る。この場合、光子は確実に下のスリットを通ってきているはずなのだが、「上のスリットが空いているのか空いていないのか」ということを知っているかのご
とく、それに応じて挙動が変化することになる。
観測機器などの状況設定によって、光の粒子性が顕著になったり、波動性が顕著になったりす
る。ここでは詳しく述べないが、たとえばスリットの片側に光が通過するかどうかの測定器をつけたりすると、この干渉縞は消失してしまう。このように、「何
を観測しようとするか」によって観測される側の状態が変わってしまうというのが量子力学のややこしいところである7。
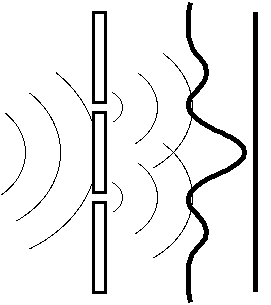ここで起こったことをもう一度よく考えてみる。二つのスリットを通る時の電子は、両方を通るような波として広がっている。そして通り抜けた後は、図で太
い線で表したような、二つの波の干渉の結果としてできあがる波がスクリーンに到達する。ところが、スクリーンに到着する光子は一個であって、ある一カ所に
しか光子は存在しなくなってしまう。
ここでスクリーンで起こっている現象を考えよう。スクリーンに当たる直前の光は、左図の上のような状態、つまり干渉を起こした波の状態であったはずであ
る。ところがスクリーンに当たると、粒子性が顔を出して一点のみに光子がぶつかる。広がっていたはずの波がいっきに一点に縮まってしまう、ということで、
このような現象を「波束の収縮」と呼ぶ。
収縮が起こるメカニズムについてはよくわかっていないが、そういうことが起こっていると解釈しなければならないような現象が起こっていることは確かである8。
大事なことは、どこに収縮するのかを決める方法がないということである。残念ながら量子力学で計算できるのは確率だけなのである。後でくわしく学ぶが、量
子力学の計算を正しく用いれば波の形が計算できる。波の振幅が大きくなっている部分(つまり「明」となる部分)に収縮する確率が大きく、振幅が小さい部分
(「暗」部)に収縮する確率は小さいのである。
確率だけしか計算できない、ということについてはもちろん批判者も多く、量子力学は不完全であるとの主張がよくされてきた。その筆頭はアインシュタインであって、彼の「神はサイコロ遊びをしない」と
いう言葉は有名である。アインシュタインは「量子力学の計算の中には入ってこないだけで、粒子がどこにいるかは最初から決まっているはずだ」という考え方
をしていた。この考え方を「隠れた変数の理論」と呼ぶ。しかしこの隠れた変数の理論とは矛盾する実験結果がある。どうやら光子の位置を観測するまでは光子
の位置は決まっていないと考えなくてはいけないらしい。
1.3 これからの学習で注意すべきこと
この章では、量子力学の「あらすじ」を述べた。初めてこのような話を聞いた人にとっては、` 非常識'と感じられるだろう。しかし、我々の` 常識'は「光が粒子の集まりであることを実感することがあまりない世界(我々が見る光源はたいてい１秒に1020個以上の光子を出している)」で作られたものである。実験が進むことによって知識が増え、世界が広がれば、常識というものは必然的に変わっていく。「光は粒子である」という実験結果が出た以上は、新しい「常識」を作らなくてはいけない。
ボーアは
「量子力学に衝撃を受けないとしたら、それは量子力学を理解してない証拠だ」
という意味のことを言っている。だから、この「あらすじ」を聞いて「そうか、量子力学ってそういうものなのか」とわかったような気がしたとしたら、
それは錯覚である。
これからの１年間の講義の中で、量子力学に衝撃を受け、量子力学の不思議さを感じて欲しい。量子力学の不思議さはすなわち、我々の住
んでいるこの世界の不思議さである。我々の住んでいるこの世界は、量子力学を知らない人が漠然と思っているよりもずっとずっと、不可思議なからくりを持っ
ている。それを解き明かしていき、理解していくことこそが物理の勉強である。
また、今回は概要だけを述べたわけであるが、物理を学ぶ者は、
自分で手を動かして納得するまでは、何事も信じ込んではいけない。
ということを肝に命じておこう。先生の説明を聞いてわかったような気になっただけでは、実はまだまだ何もわかってない9。まして概要をかいつまんで述べただけの講義を聞いて納得してはいけない。
次の章からしばらくは、歴史をたどりながら、この不思議な量子力学がどのように建設されていったかを学ぶ。
演習問題は、「初等量子力学演習」で使う。演習を受けてない人は自習しておこう。
[演習問題1-1]
紫外線(波長が5×10-8m)と赤外線(波長が1×10-6m)の一個の光子の持つエネルギーと、水素原子のイオン化エネルギー13.6eVを比較せよ。これは何を意味するか。
(注：1eVは1.6×10-19J)
[演習問題1-2]
カップ焼きそばを一杯(150グラム)食べると、約750キロカロリーのエネルギーを摂取することができる。計算を簡単にするためにすべて炭素(分子量12)でできているとする。炭素原子一個あたり、何Jのエネルギーをもっていることになるか。
(注：1カロリーは約4.2J。アボガドロ数は6.0×1023)
この値はだいたい、生物が生活していく上で起こる化学変化でやりとりされる分子一個あたりのエネルギーである。このエネルギーが光子一個になったとすると、振動数がどのくらいの光となるか。この振動数がおおむね可視光の振動数と近いことには、どんな意味があるか。
[演習問題1-3]
100Wの電球が波長5×10-7mの光を出しているとすると、この電球が１秒間に出している光のエネルギーはhnを単位として何個分と考えられるか。光速は3×108m/sである。
また、この電球の1メートル向こうで断面積0.5cm2の瞳でこの光を見たとすると、瞳に飛込む光子は1秒に何個か。
[演習問題1-4]
0等星の照度は2.5×10-6ルクスである。1ルクスは1平方メートルあたり[1/683]ワットのエネルギー流に対応する。人間の瞳の広さを0.5cm2として、瞳から入ってくるエネルギーを考え、そのエネルギーが眼の水晶体(レンズ)によって視細胞一個(半径10-6mの球とする)に集められたとする。光を波動と考えた場合、視細胞にある感光物質(ロドプシン)の1原子(半径10-10mとしよう)が化学反応するエネルギー(5×10-19Jとしよう) を得るには何秒かかるか。
[演習問題1-5]
「光が粒でやってきていて、連続的な波ではないから、星の光がまたたいて見えるのではないか？」と言った人がいる。これがほんとうかどうか、つまり星のまたたきは光子の粒子性によるものかどうかを考察せよ。
学生からの質問&コメント
大きさも質量もないのに、光子は物を通過しないのか不思議。
光は電場と磁場でできていて、物質は電場や磁場と相互作用するからです。逆に言うと、質量があったとしても電場や磁場と相互作用しないものはなんでも通過してしまいます（ニュートリノという粒子がそう）。
光の粒子は質量がないのになぜ力を及ぼすことができるのですか？
上の繰り返しになりますが、光というのは結局電場と磁場だからです。電場や磁場はクーロン力やローレンツ力という力を生み出すことができますね。
赤外線や紫外線などで物体を温めることができるのですが、逆に冷やすことができますか？
できません・・・と言いたいところですが、レーザークーリングという、光で物を冷やす技術はあります。その原理は量子力学なのです。今はまだ説明できませんが、後で話すことができるかもしれません。
光が〜〜〜じゃなくてまっすぐ進むのはわかるんですが、じゃあ山と谷って何なんでしょう？
光は電場と磁場と波（電磁波）です。つまり山と言うのは、その場所の電場（磁場でもいい）が＋向きだということで、谷は−向きだちうことです。±の定義は適当です。
スリットの干渉は波で考えると理解できたのだが、粒子で考えた場合はなぜ縞模様となるのかを、もう少し説明してほしいです。
あわてないで。その説明には前期の授業全部ぐらいがいります。
波長が長い赤色の夕日が大きく見えることがあるのは、光が広がりの性質を持っているからですか？
残念ながら違います。夕日が大きいのは対象物（山とかビルとか）が近くにあるという心理的効果が一番大きいのです。
ちなみに夕日が赤いのは空気中で波長の短い青い光がよく散乱し、波長の長い青い光はあまり散乱しないからです。波長が短いと広がりやすいという性質がここでも効いています。
光を粒として考えた時、光の粒については慣性質量と重力質量が違うということでしょうか。
いえ、それはちょっと違います。「質量」という言葉の定義をちゃんとしないといけないので、それは相対論の講義を待ってください。気をつけておいてほしいことは、「質量がない」ということと「物を押せない」ということは同じではないということです。
<> ヤングの実験で、二つの光が消し合っている部分がよくわからない。粒子だからそこに飛んでいっているのに、光子の跡がついていない。何か気持ちの悪い話だと思う。
確かに気持ちの悪い話です。気持ちが悪くなるのは当然なので安心してください。その気持ち悪さを通り抜けた後、量子力学がわかるようになります（たぶん）。
量子力学は難しいらしいので、心配です（同様のコメント多数）
たしかに難しい。難しいのでしばらくは「昔の人がこの難しい量子力学とどのように戦ったのか、そしてどのように量子力学ができあがったのか」という筋書きで話をしていくつもりです。一〇〇年前の物理学者たちの苦悩を感じ取りながら勉強してください。
脚注:
1勘違いしている人が多いが、相対論は古典力学である。物理の世界で「古典力学」と言ったら「量子力学ではない」という意味。
2プランクがどのような根拠を持ってこの主張を行ったか、およびそれがどのように正当化されるかについては次の章で述べる。
3この広がり具合は波の波長に比例するが、光の波長は10-7mのオーダーであるから、日常において広がりはほとんど見えない。一方、音の波長は1mのオーダーであるから、音の広がりは日常でもよくわかる。
4念のために書いておくと、紫外線によって起こった化学変化が日焼けそのものではない。人間の体が紫外線によって起こされた化学変化に反応した結果が日焼けである。肌が黒くなるのは、人間の体の持っている防衛機構である。
5スリットの幅が狭いがゆえに通り抜けた光は直進せず、回折して広がる。
6可視光であっても弱い光を使ってこの条件を満たすことはできる。また、エックス線をつかってガイガー管などで計測すれば、一個の光子を測定することも可能である
7と書いたが、観測機器によって状態が乱されるということ自体は、古典力学的状況であっても同様である。量子力学では少々劇的になっているというだけのこと
8この現象をどう解釈するかについては諸説があるが、ややこしくなるのでここでは触れない。
9これはもちろん、前野の自戒が込められた言葉である。
File translated from
TEX
by
TTH,
version 3.67.(TTHの出力をmozilla composerで編集しています）
On 15 Apr 2005, 12:23.
