試験問題解説
今日は7月26日にやった試験の解説と講評です。

答えはここをクリック
基本的概念を問うただけなのだが、正解率はよくなかった。特に悪かったのは
系をある状態$(T;V,N)$から別の状態$(T';V',N)$へと様々な断熱操作で変化させた。このときに系のする仕事は準静的でも準静的でなくても同じである。
が答えられないもの。準静的かそうでないかには関係なく、断熱操作では始状態と終状態が同じなら仕事は同じ、というのは熱力学の要請である。このあたりから間違っているようでは先が思いやられる。

答えはここをクリック
これは、(ウ)のみが起こり得る現象である。系が負の仕事をした後なら、温度が上がっている可能性があるからである。(ア)と(イ)はエントロピー増大則から起きないし、(エ)は示量変数がもとに戻っていることから、プランクの原理により起こり得ない。

答えはここをクリック
(1)については「途中ではピストンの動きについていけず、気体の圧力が下がっている。このために仕事は小さくなる。」ということが書いてあればよい。
(2)この状態から準静的に元に戻すと、気体は$-W_{\rm max}$の仕事をする。最初にした仕事を$w$とするとこのサイクルで気体のする仕事は$w-W_{\rm max}$だが、Kelvinの原理からこれは0以下である。よって$w < W_{\rm max}$である。Kelvinの原理を使うためにはサイクルにしなくてはいけないので、自分で「元に戻す操作」を付け加える必要があるが、これをやらずにただ「Kelvinの原理から」で説明した気になっている答案があったが、それでは説明になってない。
答えはここをクリック
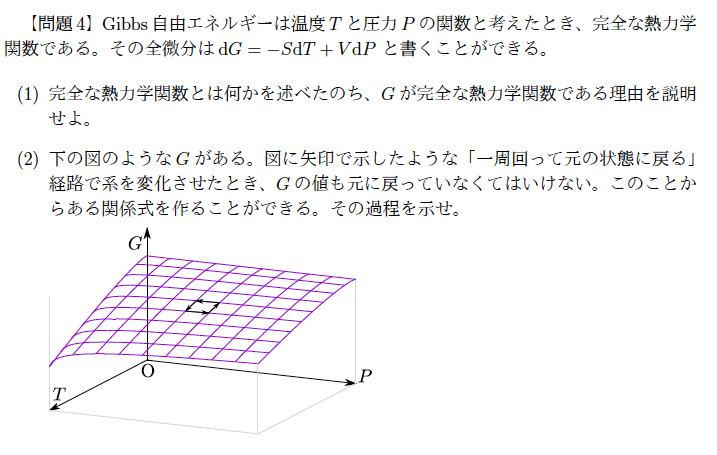
(1)その関数を知ることで熱力学で得るべき情報を全部得ることができるのが「完全な熱力学関数」である。$G$を知れば、$S,V$は$G$を偏微分することで知ることができるから、$G$は完全な熱力学関数である。
【誤答】「最小値が求まる関数」とか「凸関数」とかの答えがあったが、これらは完全な熱力学関数とは全く別物。
(2)Maxwell関係式を出す問題。${\partial G\over\partial T}=-S$と${\partial G\over\partial P}=V$が読み取れるから、「$T$で微分したものを$P$で微分したもの」と「$P$で微分したものを$T$で微分したもの」が等しいとおけば、 $$ -{\partial S\over\partial P}={\partial V\over\partial T} $$ という式になる。

答えはここをクリック
(1) 2つの答え方があって、「周りの空気の温度が上がっているから、実は全体のエントロピーは増えている」と指摘するか、「断熱操作ではないからエントロピー増大則の適用範囲外」と指摘するか。後者の答えが多かったが、前者の答え方の方がより丁寧に現象を説明している。
(2) 2つのエネルギーは、考えている操作が違う($F$は等温準静的操作で、$U$は断熱操作)。よって比較すること自体、意味がない。
(3) 「室外機のないクーラー」は断熱操作で温度を下げることになるから、プランクの原理によりありえない。技術が進歩したらどうなるというものではない。

答えはここをクリック
(1) $\diff U=cNR\diff T$、$P={NRT\over V}$として$\diff S={1\over T}\diff U+{P\over T}\diff V$に代入すると、 $$ \diff S= {cNR\over T}\diff T+{NR\over V}\diff V $$ となり、これを積分して、 $$ S=cNR\log T+ NR\log V+S_0 $$ となる。
(2) $\diff U=4\alpha T^3 V\diff T+\alpha T^4\diff V$で $$ \begin{array}{rl} \diff S=&{1\over T}\left(4\alpha T^3 V\diff T+\alpha T^4\diff V\right)+\left({1\over 3}\alpha T^3\right)\diff V\\ \diff S=&4\alpha T^2 V \diff T +{4\over 3}\alpha T^3 \diff V\\ \diff S=&{4\over 3}\alpha\diff \left(T^3V\right)\\ S=&{4\over 3}\alpha T^3 V + S_0 \end{array} $$ となる($S_0$は積分定数)
なお、$\int 4\alpha T^2 V\diff T={4\over 3}\alpha T^3V$および$\int {4\over 3}\alpha T^3 \diff V= {4\over 3}\alpha T^3V$と積分したつもりで答えを${8\over 3}\alpha T^3 V + S_0$としている答案があったが、これはだめ($T$も$V$も定数じゃないから)。逆に${8\over 3}\alpha T^3 V$を微分したら$4\alpha T^2 V \diff T +{4\over 3}\alpha T^3 \diff V$には戻らない。

答えはここをクリック
(1) $U(T,V)=F(T,V)+TS(T,V)$を($T$を一定にして)$V$で微分すると、 $$ {\partial U(T,V)\over\partial V}=\underbrace{{\partial F(T,V)\over \partial V}}_{-P}+T{\partial S(T,V)\over \partial V} $$ となり、ここでMaxwellの関係式から、${\partial S(T,V)\over \partial V}={\partial P(T,V)\over\partial T}$を使うと、 $$ {\partial U(T,V)\over\partial V}=-P-T{\partial P(T,V)\over \partial T} $$ となる。理想気体の状態方程式を使うと、右辺は0。
(2) $TV^\alpha$が一定という式を微分して、$\diff T V^\alpha + \alpha TV^{\alpha-1}\diff V=0$がわかる。これから$\diff V=-{V\over \alpha T}\diff T$なので、$\diff U={pV\over T}{1\over \alpha}\diff T={NR\over \alpha}\diff T$となる。積分して、$U={NR\over \alpha}T+C$となる。境界条件より積分定数は0なので、$U={NR\over \alpha}\diff T$

答えはここをクリック
(1) $0=\diff S=(U-F)\times\left(-{\diff T\over T^2}\right)+{1\over T}(\diff U-\diff F)$に$\diff U=-P\diff V$を代入すると、$0=-{U-F\over T}{\diff T\over T}+{1\over T}(-P\diff V-\diff F)$となって、これから$\diff F=-S\diff T-P\diff V$
(2) $0=\diff T=(U-F)\times\left(-{\diff S\over S^2}\right)+{1\over S}(\diff U-\diff F)$に$\diff F=-P\diff V$を代入すると、$0=-{U-F\over S}{\diff S\over S}+{1\over S}(\diff U+P\diff V)$となって、これから$\diff U=T\diff S-P\diff V$

答えはここをクリック
(1) $p={NRT\over V}$なので、$\int_{V_1}^{V_2}p\diff V=NRT\int_{V_1}^{V_2}{\diff V\over V-b}=NRT\log\left({V_2-b\over V_1-b}\right)$
(2) $\Delta U=Q-W$で、$W$が上の答え。$\Delta U=0$(等温だから)。よって上の答えそのものである。
(3) 始状態と終状態で温度が変化してないから、$\Delta U=0$、断熱操作なので $Q=0$だから、仕事も0。
(4) 断熱操作だから、$\diff U=-p\diff V$となり、$Nc\diff T=-{NRT\over V-b}\diff V$という式が成立する。変数分離して$c{\diff T\over T}=-R{\diff V\over V-b}$なので積分して、$c\log T=-R\log (V-b)$となり、一定となるのは$T^c (V-b)^R$という量(または、$T(V-b)^{R\over c}$などでもよい)。あるいは状態方程式から$T={p(V-b)\over NR}$だから、$p(V-b)^{1+{R\over c}}$が一定。
答えはここをクリック
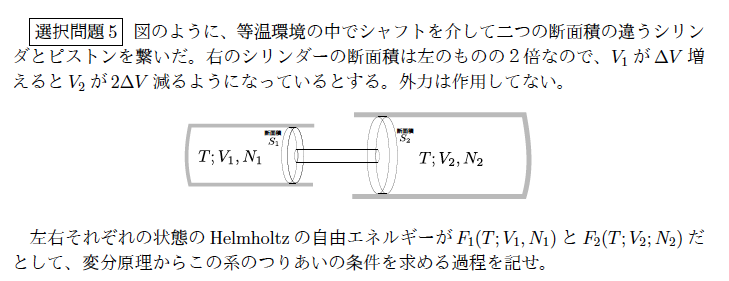
極小となるべきは、 $$ F_1(T;V_1+\Delta V,N_1)+F_2(T;V_2-2\Delta V,N_2) $$ なので、これを$\Delta V$で微分して0と置くと、 $$ {\partial F_1(T;V_1,N_1)\over \partial V_1}-2{\partial F_2(T;V_2-2\Delta V,N_2)\over\partial V_2}=0 $$ となり、左の圧力が右の2倍、という答えが出る。

答えはここをクリック
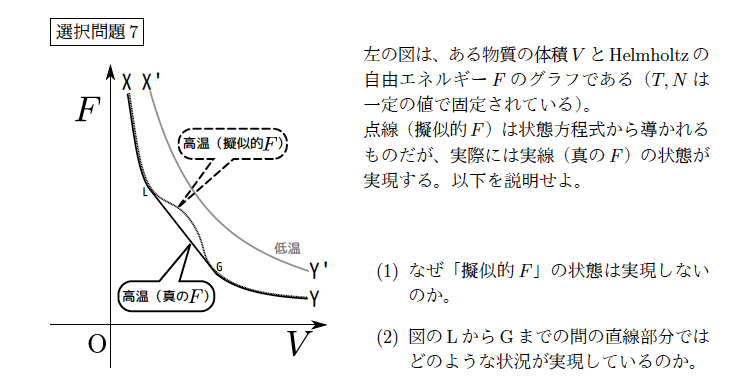
最初のHelmholtz自由エネルギーは、 $$ \begin{array}{rl} &cN_1RT-NRT\log\left({T^cV_1\over N_1}\right)\\ +&cN_2RT-NRT\log\left({T^cV_2\over N_2}\right) \end{array} $$ であり、終状態では $$ c(N_1+N_2)RT-NRT\log\left({T^c(V_1+V_2)\over (N_1+N_2)}\right) $$ となる。できる仕事はこの差となり、 $$ W= N_1RT\log\left({(V_1+V_2)\over (N_1+N_2)}\times{N_1\over V_1}\right) +N_2RT\log\left({(V_1+V_2)\over (N_1+N_2)}\times{N_2\over V_2}\right) $$ となる。これが0になるのは、${N_1\over V_1}={N_2\over V_2}={N_1+N_2\over V_1+V_2}$のとき。つまり、密度が最初から等しく、始状態と終状態で密度が変化しない場合である。
答えはここをクリック

答えはここをクリック
(1) $H(T,p;N)=G(T,p;N)+TS(T,p,N)$の両辺を$T$で微分する。 $$ {\partial H(T,p;N)\over \partial T}={\partial G(T,p;N)\over\partial T}+S(T,p,N)+T{\partial S(T,p;N)\over \partial T} $$ となるが、やはり右辺第一項と第2項が消える。
(2) 両辺を$T$で微分する。右辺第1項の微分では、第1引数の微分と第2微分の引数の二つが出る。すなわち、 $$ {\partial\over \partial T}F[T;V(T,p;N),N]={\partial F\over \partial T}+{\partial F\over \partial V}{\partial V\over \partial T} $$ となる。この結果の第2項は$-p{\partial V\over \partial T}$となるので、後から出てくるものと消える。