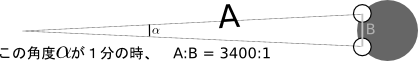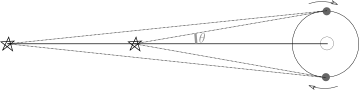確認テスト1
今回の授業への感想をどうぞ。
要望などがあったら書いてくれてもいいです(要望に応えるかどうかは場合によります)。
テストと言いつつ、1は単なる感想でした。いくつか代表的な感想と、質問などで返事できるものに返事しておきます。
授業内容に関連した物理学の豆知識や雑学を挟んでいただけると、記憶にも残りやすいためありがたいです
関係する話はついついしゃべってしまうと思います。
私はオンデマンドでの授業が初めてであったため、とても新鮮に感じました。この授業ではわからないことを何度も見直すことができる点がとても素晴らしいと感じました。また、図やアプリケーションを多用して授業が行われているため、視覚的にわかることができました。
読み返し、見返ししながら、あとアプリで遊びながら、いろいろ理解していってください。
昔の人が行う遠い距離の測り方などは疑問に思っていたし初めて知ることができたのでとても為になった。月と地球と太陽の大きさを比べるアプリを見て実際どれくらい大きさに違いがあるのか知れてよかった。
ものすごく遠くにあるものの大きさを知るってのはなかなかむつかしいですね。
月があんなに小さく見えてるなんてすごく驚きました。
「月が小さい」ということを実感するには、写真を撮ってみるのが一番です。「あれ、写真だとこんなに小さいの?」と思えます。人間の眼は騙されても、カメラは騙されない。
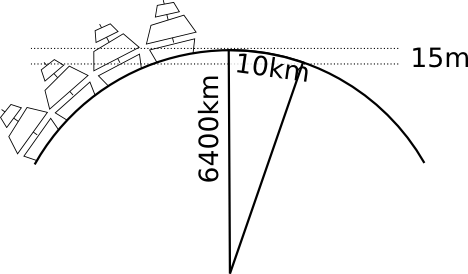
「•••このような水平をちゃんと測る技術ができてからでないと、地球が丸いことには気が付きません」とありますがそれはなぜでしょうか?
地球が丸い原因に万有引力が関係していることは知っています。
丸い原因の話をしているんじゃなくて、人間が丸いことに気付けるかどうか、という話です。我々は学校で習ったから「地球は丸い」と知っているけど、日常生活ではそれは気付けないでしょう? それがわかるためには、回りの見えているものを正確に測定する必要があるのです。
そしてその後に{•••人間が直観的に理解できるスケールに比べて、この差はかなり「微妙」です}とありますがこの際の微妙とは人間にとってはあまりにも小さな変化すぎるということでしょうか?
はいそういうことです。
私は、インターステラー_というSF映画が大好きで、何度も見るほどである。しかし、「時間」や「空間」を題材にしており一向に理解ができない。が、この講義を受ければ、少しでも理解に近づけられるのではないかと感じ、期待とワクワクがこみあげる授業であった。
「インターステラー」は物理学者も協力していて、なかなかおもしろい映画ですね。映画そのものではないけど、似たような話もしたいと思ってます。
高校の卒業研究でブラックホールについて少し調べたことがあるので、今後の授業で学ぶであろう相対性理論や重力と時間と空間の関係をさらに詳しく学びたいです。
ブラックホールの話もそのうちやります。
地球は丸いという話題のところで気になったことがありました。それは標高はどうやって測っているのかということです。海面の高さを0とした時の海抜ということはなんとなくわかるのですが、ユーラシア大陸の真ん中らへんの標高はどこの海面を基準に測っているのですか?
「海面」ってどう定義するかが難しいところですね。実は地球は完全な球ではないので、どこが「海面」なのかは結構複雑です。標高を決めるには海面を(仮想的に)大陸の下まで延長していくんですが、そのとき「重力と垂直な方向」を水平と見て、水平な方向に伸ばしていく(こうやって求めた面を「等ポテンシャル面」とか「ジオイド」とか呼びます)という方法を取ります。「重力の方向」は「真下」なので、「真下と直角」なら「水平」と考えるわけです。
授業の資料がずっとぐるぐるして見れなかったです。
すいません、なんかトラブルがあったみたいです。こういうのは感想に書いても月曜日まで見ないので、連絡用掲示板をwebClassに作ったのでそこに書いてください。
動画で画面が全部黒いところがあって何を説明しているのか分かりずらかったです
どこのことかな?? こういうのも、具体的にここがこう、と掲示板の方で報告してくれたらすぐ対応します(感想は月曜日にまとめて見ているので)。
確認テスト2
月と太陽を地球からみた見かけの大きさは、だいたい同じです。
月と太陽とが同じ距離になる場所(ただしどちらも円に見える程度は近い)に行ったら、どっちが大きく見えるでしょう。
さすがにほとんどの人が正解でしたが、「月」と答えた人が2名、「どちらも同じ」と答えた人が1名いました。正解はもちろん「太陽」です。
確認テスト3
月が太陽を隠すと日食になりますが、太陽が月を隠すことは有り得るでしょうか。
- 有り得る。それが月食である。
- 有り得る。夜太陽が見えないのは月に隠れているからである。
- 有り得ない。地球からの距離は太陽の方が遠いから。
- 有り得ない。月の方がサイズが大きいから。
76名3.「有り得ない。地球からの距離は太陽の方が遠いから。」(正解)を選んでましたが、1.「有り得る。それが月食である」と答えた人が7名いました。月食というのは隠れるんじゃなくて「影を落とす」現象ですね。
確認テスト4
月の上に見る太陽は、地球から見る太陽より大きいだろうか、小さいだろうか。
- 見てすぐわかるほどに、すごく大きい
- 見てすぐわかるほどに、すごく小さい
- 時間により、大きかったり小さかったりすることが、見てすぐわかる。
- 時間により、大きかったり小さかったりするのだが、見てすぐわかるほどの変化じゃない。
ちょっと難しかったかな?? アニメーションを見てもらうとわかるように、月と太陽の距離は、月が地球の回りを回っている分だけ近くなったり遠くなったりするので、大きくなったり小さくなったりはするのですが、太陽・地球間の距離が地球の直径の11726倍に対して地球・月間の距離は30.2倍なので、11726+30と11726-30の違い程度にしか大きさは変化しません。というわけで、4.「見てすぐわかるほどの変化じゃない。」が正解です。83%が正解でした。
今、あなたはゆいレールが走っている場所の近くにいる。物差しを使わずに、ゆいレールの車両が地上何メートルの高さにあるかを測る方法をどんなものでもよいので考えてください。
最後は少しだけ頭を使ってもらう問題でした。以下は皆さんの解答の一例です。
ゆいレールの軌道の直下地点から直線で任意の距離の場所に立ち、その場所から車両を見上げた際の角度aを測定する。三角比を用いて、ゆいレールから立っている場所までの距離に角度a°tanを掛けると車両の高さを求めることができる。
のような感じの解答が多いかなと予想して出した問題です(もちろんこれ以外でもちゃんと考えて説明がされていれば正解です)が、このように三角比を使うという解答が多かったですね。なお、
三角測量を使う。
みたいな説明不足なものは少しだけ減点しました。
三角測量でも、
ゆいレールから地上の2点を見下ろして、その2点の距離と、2点と見下ろした場所との角度を求めて、計算によって高さを導く。
とか、
まず自分の手でアロハポーズをとる。親指から小指の長さは自分で大体わかっているからである。そしてゆいレールの真下に車を置く。車の車高をアロハポーズで測る。そして車がちょうどアロハポーズで収まるところまで離れる。そしたらゆいレールがアロハポーズ(車)何個分か測る。最後は普通に計算したり対比を用いて求める。
とか、ちょっと違う方向で考えている人もいました。これもよさそうです。
ゆいレールの真下に立ち、自分の影の長さとゆいレールの影の長さの比率を見る。続いて、自分の身長にその比率をかけるとおおよその高さがわかる。
のように、影を使うという案もいくつかありました。
ゆいレールを支えている柱のところに自分が立ち、写真を撮って、自分の身長から何倍かを求めて高さを測る。
のように写真を使う手を考えてくれた人もいました。
自分の身長が分かれば相似を用いて求められる。
とだけ書いていた人もいて、なんとなく気持ちはわかるけど、もう少し説明はほしいかな。
ビルや建物の一階あたりの高さが大体3-4Mである。ゆいレールは大体オフィス街や周りに建物がある所を通るため、近くのビルの大体何階辺りにゆいレール車両があるかを見て高さを推測する。
という案もありました。だいたいの目安としてはこれで大丈夫な気もします。
ゆいレールに乗るためには階段を上る必要があり、その全段はだいたいゆいレールの高さに等しい。なので階段一段がだいたい何センチかを自分の手のひらなどで測り予測して、階段の段数をかけることでおおまかなゆいレールの高さがわかる。
のような直接的な測定を考えていた人もいました。
ボールや軽い物を使って、ゆいレールの車両から地面までの落下時間を測定し、その時間を使って高さを計算します。
- ゆいレールの真下に立ち、ボールを真下に落とすと仮定します。
- 落下時間をストップウォッチやスマートフォンのアプリで計測します。
- 重力加速度の公式を使い、高さを計算します。
のように物を落とす方法を考えている人も何人かいました。これはこれで面白そうですが、実際に物を落とすときは空気抵抗が聞いてくるので加速度運動の公式どおりにいかない可能性があることは考えなくてはいけないでしょう。
1000円札の横の長さが15センチメートルであるため、ゆいレールの柱にびっしりと1000円札を並べて、その枚数で長さを測る。
というなかなかすごい案もあったけど、ゆいレールの柱に1000円札並べるのは、大変だし、高いから危ないと思う。