波の反射／透過
これは、波が１次元的に進行してきた波が境界面で反射／境界面を透過する様子を示すアニメーションである。説明はプログラムの下の方にある。
振動数ν= 角振動数ω= 波数k= 速度v=
最初は、↑のセレクトボックスに書いてあるように「固定端反射」の場合の動くグラフが出ている。
固定端反射とは
（図では中央にある）反射点(x=0)において合成波の変位が0になる（つまり、合成波がx=0で固定されている）場合の波の反射である。合成波は実際にこの場所で観測される波であり、入射波と反射波の重ねあわせでできている。数式で表現すると
入射波：y入= A sin( kx-ωt )
反射波：y反= -A sin( -kx-ωt ) = A sin( -kx-ωt +π)
となる。ここで、kは波数で（2π÷波長）、ωは角振動数で（2π÷周期）である。このような式になっていると、x=0においてy入+y反=0になる。しばしば、「固定端反射では位相がπずれる」と表現されるが、それはx=0における波を、y入= A sin( -ωt )とy反= A sin( -ωt +π)のように表現することができるからである。
自由端反射とは
自由端反射とは固定端とは逆に、反射点(x=0)が「自由に」動くことができる場合の波の反射である。自由という名前がついているが反射波が何でもよいという意味で自由なのではない。
入射波：y入= A sin( kx-ωt )
反射波：y反= A sin( -kx-ωt )
のように、今度は位相がずれない、という形で反射する。こうすることで、x=0において
| ∂ ∂x | (y入+y反)=0 |
という条件が満たされる。この条件の意味するところは x=0において合成波が平坦（傾き０）になれ ということである。上のアニメーションで実際そうなっていることを確認しよう。
屈折率と反射の仕方はどう関係するのか？
となっている時は波は境界（x=0）で跳ね返されるのではなく、内部にも進入し、透過波になる。
まず、「屈折率」という言葉の意味から説明しよう。x>0の領域とx<0の領域で（たとえばその場所での波の媒質が違うなどの理由で）波長（波数）が変化する場合がある。境界（x=0）を超えることで波長が(1/n)場合になる場合（つまり、波数kがn倍になる場合）、「屈折率=n」と表現する。つまり
| 屈折率n= | 入射波の波長 透過波の波長 |
である。上にあるスライダーを動かして屈折率を変化させ、状況を確認しよう。ここで大事なことは入射波と透過波が境界x=0でつながっているだけではなく、その傾きもちゃんと接続されているということである。
屈折率を変化させて状況を確認して欲しいが、
屈折率nが大きい時は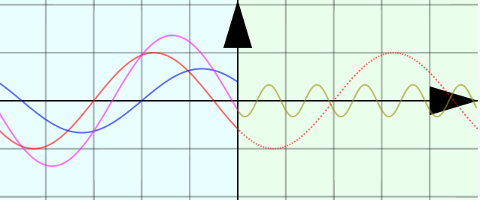
のように、
屈折率nが小さい時は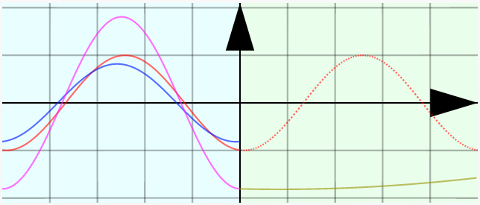
のようになる。
屈折率nが小さい時は「自由端」に近い形になっていることがわかるだろうか？---右側（透過後）では波長が長くなるのだから、左側（透過前）よりも平坦に近い波になり、これと接続されなくてはいけないから、自由端の場合に似た反射になるのである（屈折率nが大きい時はこの逆で、固定端に似た反射になる）。
式で表現しておくと、屈折率nの場合の波の式は、
| 反射波：y反=A | 1-n 1+n | sin( -kx-ωt ) |
| 透過波：y透=A | 2 1+n | sin( nkx-ωt ) |
である。ここで反射波の係数に1-nが含まれているために屈折率nが1より大きいかどうかで反射波の位相がπずれるかずれないかが決まる。