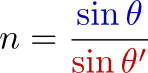波の屈折:スネルの式
まず最初に、「屈折の法則(スネルの式)」を実感しよう。
屈折の法則(スネルの式)は、
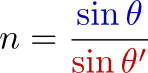
という式である。ここでθは上に示した角度で「入射角」と呼び、θ'も同じく図に示した角度で「屈折角」と呼ぶ。動いている緑の線は、波の「山」を表す線(波面)である。
屈折角 θ'=14.4775...
速度v=1m/s
上のスライダで波長λ、周期T、入射角θと屈折率nを変えることができる(屈折角θ'はこの二つに応じて変わる)。特に入射角と屈折率をいろいろと変化させて様子を見よう。
nが1だと曲がらない。
nが1より大きいと、大きいほどよく曲がる。
nが1より小さいと、小さいほどよく曲がる。
ということがわかったであろうか?
上の図の中央に描かれた円は単位円(半径1)なので、aと書いた長さがちょうどsinθ、bと書いた長さがちょうどsinθ'である。この二つの比が屈折率nである(図を見て、動かしながら確認しよう)。
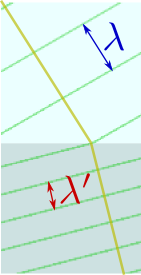
屈折率とはいったいどのような物理量で、どうしてこういう法則が成り立つのだろうか?---上の図でnを変化させた時に変わるものを見ていくと、左の図に示した、上と下での波長(λとλ')の比であることがわかる(これも図を動かしながら確認しよう)。
| つまり、屈折率とは、 | 境界を超える前の波の波長λ
境界を超えた後の波の波長λ' | で計算される量なのである。 |
ここで念のため注意しておくが、屈折すると波長が変わるのではない。
波長が変わることが屈折の原因なのである。
このことの説明の方法はいろいろあるが、まずは上の図をじっくり見て、
上と下で波長が違いつつ、かつ山の線(波面)がちゃんとつながるようになるためには、波の進行方向(波面の進む向き)が変わらなくてはいけない。
ということを実感して欲しいとおもう。
ホイヘンスの原理による波の直進
屈折率の意味は波長の変化の割合であるが、波長の変化により波が屈折する(曲がる)ことは、ホイヘンスの原理を使って説明することができる。
ホイヘンスの原理とは、以下のように考えることである瞬間の波面からしばらく後での波面を知る方法である。
ある瞬間の波面(波の山)の各点各点が素元波とよばれる小さい波を発生させる。素元波は(点から出ているので)球面状に広がる(ここでは平面図で表現してるので、球面状ではなく円形状に広がる)。
ある瞬間の波面の各点から出た素元波を重ねあわせ時、素元波の波面の包絡線が新しい波面になる。
では、まずは屈折せずに直進している波の場合でホイヘンスの原理を実感することにしよう。説明は動く図の下にある。
振動数=14.4775...
速度v=1m/s
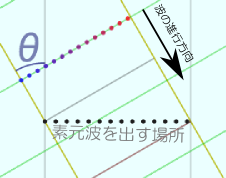
上の図が何を表しているかを説明しよう。
ホイヘンスの原理における「素元波」はありとあらゆる場所から出ているのだが、それを全部表示していると重なって何がなんだかわからなくなるので、図で素元波を出す場所と書いた直線の上から出る素元波だけを見ることにする。
左の図は波が素元波を出す場所に向かって進んでくる様子を示したもので、色のついた●は波の「山」を表す。この波の山が波の進行方向に移動してきて、素元波を出す場所にあたるとその点を中心として素元波を出す。
その素元波のあつまりがどのような波面を作るか、上の動く図を見ながら確認して欲しい。それぞれの場所から同時に同じ速さで素元波(平面で考えているので円状になる)が広がっていく。
なお、通常ホイヘンスの原理で直進する波の説明をする時は素元波を出す場所を波面に沿って並べることが多い。上の図でそのようにしたければ、θ=0にすればよい。その場合、素元波を出す場所は波面と平行な線になり、波の山は同じ時刻にこの線に到着することになる。
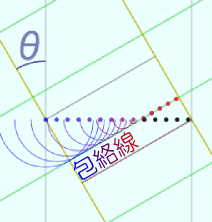
この広がっていく素元波の円を重ねた時の、円を外から包み込むような線が包絡線(右の図)であり、この包絡線のところに新しい「波の山」ができる、というのがホイヘンスの原理である。
いろいろ角度などを変えて試して欲しい。素元波によって作られる「新しい波面」は「最初の波面」と平行であること、そして波の進む方向はその波面と垂直であることがわかる。
ただし、ここまでではホイヘンスの原理の威力というのはあまりわからないだろう。次のページで屈折の法則をホイヘンスの原理を使って理解していこう。
なお、ホイヘンスの原理では「後ろ向きに進む波がなぜないのか」は説明できない(図ではあえて後向の波を表示してない)。ホイヘンスの原理はそもそも波の進む向きを決めるこごとができない法則なので、それは仕方ない。
ホイヘンスの原理から理解する波の屈折
屈折が起こるのは境界面を通り過ぎたことで波の波長や速度が変化するときである。次の図はそのような場合のホイヘンスの原理を説明したものである。素元波を出す場所を境界面上に置いている。
屈折角 θ'=14.4775...
振動数=14.4775...
速度v=1m/s
進んできた波が境界面上にならんだ素元波を出す場所に当たるとそこで素元波を出すと考える。すると今度はさっきと違って、素元波が出る時期にずれが生じる(入射角θが0ならば生じないが、この図ではθは0にならないようになっている)。また、境界より先では波の速度が変化するから、波面が折れ曲がる。
全反射
屈折率、角度などをいろいろ変えて試してみよう。いろいろ試していると、「屈折した波が存在しない場合」があることに気づくと思う。この状態を全反射と言う。全反射は数式で理解するならば、スネルの式
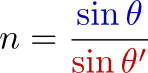
において、sinθ'が1より大きくなってしまう状況に対応している。
上の図で全反射を起こしてみると、
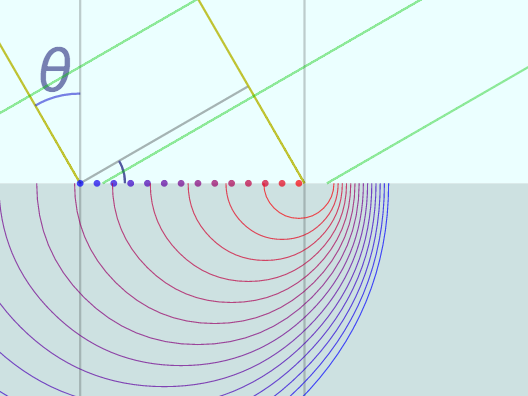
のようになって、それぞれの素元波の山が重ならず、包絡線ができない状況に対応していることがわかる。