はじめに
「微分」の理解で大きなネックとなるのが「極限」の概念。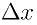 を0に近づける、と言われてもなんのこっちゃ、という感じであろう。そこで、「
を0に近づける、と言われてもなんのこっちゃ、という感じであろう。そこで、「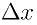 を小さくする」のではなく「グラフを拡大する」という視点でこの極限というものを理解してみよう、ということでアニメーションつきのプログラムを作ってみた。
を小さくする」のではなく「グラフを拡大する」という視点でこの極限というものを理解してみよう、ということでアニメーションつきのプログラムを作ってみた。
はじめに「微分」の理解で大きなネックとなるのが「極限」の概念。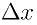 を0に近づける、と言われてもなんのこっちゃ、という感じであろう。そこで、「 を0に近づける、と言われてもなんのこっちゃ、という感じであろう。そこで、「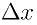 を小さくする」のではなく「グラフを拡大する」という視点でこの極限というものを理解してみよう、ということでアニメーションつきのプログラムを作ってみた。 を小さくする」のではなく「グラフを拡大する」という視点でこの極限というものを理解してみよう、ということでアニメーションつきのプログラムを作ってみた。 |
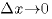 極限での傾き」を求める、という言い方をするが、それはつまり「直線とみなしても構わないぐらい拡大してから
極限での傾き」を求める、という言い方をするが、それはつまり「直線とみなしても構わないぐらい拡大してから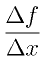 を考える」ということだと言ってもよい(厳密には極限という操作をちゃんと定義しなくてはいけないのはもちろんである。ここでは定義するというよりは「気持ち」を理解して欲しい)。
を考える」ということだと言ってもよい(厳密には極限という操作をちゃんと定義しなくてはいけないのはもちろんである。ここでは定義するというよりは「気持ち」を理解して欲しい)。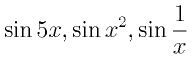 のグラフを用意している。上にある▼をクリックすると関数を変えられる。特にsin(1/x)は原点近くで激しく変化する関数だが、根気よく拡大していけば、いつかは直線のグラフに、ちゃんとなる。
のグラフを用意している。上にある▼をクリックすると関数を変えられる。特にsin(1/x)は原点近くで激しく変化する関数だが、根気よく拡大していけば、いつかは直線のグラフに、ちゃんとなる。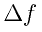 と
と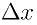 が0に近づくのに、
が0に近づくのに、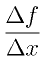 が一定って、なんか嘘くせえ」
が一定って、なんか嘘くせえ」