三角関数というのは「直角三角形の角度と辺の比」という関数としてまず定義される。 この時の角度は「度」ではなく「ラジアン」と呼ぶ単位を使うことが多い。角度を表す文字として、ギリシャ文字のθ（シータ）を使おう（こういうのはあくまで慣例であって、別に角度にどんな文字を使ったって構わない）。
直角三角形の３辺の長さは、底辺、高さ、斜辺の三つである。この三つから作られる比は６種類あるが、特に（下に書いた）三つの比がよく使われる（残り３つはその逆数である）。
| sinθ= | 高さ 斜辺 | cosθ= | 底辺 斜辺 | tanθ= | 高さ 底辺 |
以下の図の直角三角形はドラッグして動かすことができ、直角以外の頂点を動かすことで変形できる（ただし、天辺の頂点は上下にしか動かないし、底辺のうち直角でない方の点は左右にしか動かない）。点を動かしながら、それぞれの辺の比（sin,cos,tan）がどういう量かを実感しよう。
| sinθ= | = |
| cosθ= | = |
| tanθ= | = |
次に、斜辺を1に固定した直角三角形のsinとcosの値の変化の様子を次の図で実感しよう。
この図もドラッグで直角三角形を移動・変形できるが、斜辺の長さは一定になっている。角度とcosθとsinθの変化の様子を観察しよう。
この図から容易に、cos2θ+sin2θ=1となることがわかる（斜辺がつねに長さ1であることに注意せよ）。
sin,cosが正になったり負になったりするが、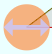
から
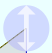に向かう方向が「上」「右」の時にsin,cosは正であり、「下」「左」の時にはsin,cosは負である。図ではそれを
や
が鏡文字になることで表現している。
次に、任意の角度でのsinとcosを以下の図のように定義しよう。ここまでで動かしてみてθという角度の意味はからに向かう方向を表すものであることがわかったと思うので、ここからはを固定して、斜辺にあたる角度の変わる部分の長さを1に固定して考える。
まず、sinθの方だけを考えることにしよう。
この図の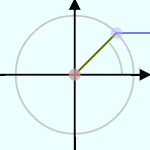
は半径１の円（単位円）を描いたもので、中心から円周の一点に向かっている棒
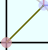の角度に応じて、sinθの値が決まる。
棒の角度はドラッグによって変えられて、
のように2πより大きい（何周も回る）角度にしたり、
のように負の角度にしたりもできるので、いろいろ変えて状況を確認して欲しい。
次に、sinθとcosθを同時に表示してみよう。さっきはθは任意の角度にしておいたが、今度は-πからπまで（-180度から180度まで）にしておく。
三角関数の「公式」として、
sin(θ+π)=-sinθ
cos(θ+π)=-cosθ
というものがある。この式がなぜ成立するか、は下の図でしばらく遊んでみればわかるのではないかと思う。
図の
の部分の薄い色になっている
の方が、θよりπラジアン（180度）大きい角度の場合の「長さ1の棒」になっている。sin,cosがπ足されることでどう変化するかを、図から読み取っていけば、公式が作られる（この公式は式として覚えようとしなくても、意味を考えればすぐにわかる）。
前ページ同様によくでてくる三角関数の公式として、
| sin(θ+ | π 2 | )= cosθ |
| cos(θ+ | π 2 | )= -sinθ |
がある。これも下の図で遊びながら理解して欲しい。
これが分かれば、
| sin(θ- | π 2 | )= -cosθ |
| cos(θ- | π 2 | )= sinθ |
の方も理解できるだろう。
のようにθが直角より大きくなり「
のようにθが負になり「