オイラー角
webGLという3Dのライブラリが動かないブラウザ環境では遅くなる場合があります。できるかぎり、webGLの使える環境で動かしてください。
剛体の運動を考えるとき、剛体が今どのような位置関係を持っているかを3つの角度を使って表現するのが「オイラー角」である。3つの角度を表す記号としてφ、θ、ψを使おう。passiveな変換、すなわち座標系の方を回す変換として説明する。図に示したように座標軸の向きを変える。下の図では、その三つの角度を変更して、どういう変換を行っているかをアニメーションで見ることができる。
回転の向きはすべて右ねじが軸の方向に進むときに右ねじが回る向きである。
x軸、y軸、z軸を回転させるパラメータがφ、θ、ψである。
φは、元々のz軸を軸として角度φの回転を行う。
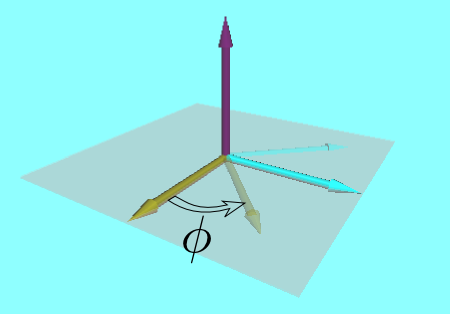これは、${\bf C}=\left(\begin{array}{ccc} \cos \phi&\sin \phi&0\\ -\sin \phi &\cos\phi&0 \\ 0&0 &1 \\ \end{array}\right)$という行列で表現される。上のスライダを動かすことで、φを変えられるので、どのような回転が起こるかを確認しよう。
次に、今の移動が終わった後のx を軸として二つ目の角度θの回転を行う。
これは、${\bf B}=\left(\begin{array}{ccc}1 &0 &0 \\0&\cos \theta&\sin \theta\\0 &-\sin \theta &\cos\theta \\\end{array}\right)$という行列で表現される。
θは、いわば「z軸をどれだけ倒すか」を決める角度である。そしてここで、φが「z軸をどの方向に倒すか」を決める角度であったことがわかる。スライダーを動かしていろいろな値にして、確認しよう。
最後に、以上二つの回転が終わった後のz軸を軸として角度ψの回転を行う。
${\bf A}=\left(\begin{array}{ccc}\cos \psi&\sin \psi&0\\-\sin \psi &\cos\psi&0 \\0&0 &1 \\\end{array}\right)$がそれを表現する行列である。
三つの操作をまとめると、 \begin{equation} \underbrace{ \left(\begin{array}{ccc} \cos \psi&\sin \psi&0\\ -\sin \psi &\cos\psi&0 \\ 0&0 &1 \\ \end{array}\right)}_{\bf A} \underbrace{ \left(\begin{array}{ccc} 1 &0 &0 \\ 0&\cos \theta&\sin \theta\\ 0 &-\sin \theta &\cos\theta \\ \end{array}\right)}_{\bf B}\underbrace{ \left(\begin{array}{ccc} \cos \phi&\sin \phi&0\\ -\sin \phi &\cos\phi&0 \\ 0&0 &1 \\ \end{array}\right)}_{\bf C}\label{EulerPassive} \end{equation} である。この行列によって$\left(\begin{array}{c}\vec{\mathbf e}_X\\ \vec{\mathbf e}_Y \\ \vec{\mathbf e}_Z\end{array}\right)={\bf ABC}\left(\begin{array}{c}\vec{\mathbf e}_x\\ \vec{\mathbf e}_y \\ \vec{\mathbf e}_z\end{array}\right)$のように座標基底ベクトルが変換される。
具体的計算結果は以下の通り。 \begin{equation} \left( \begin{array}{ccc} \cos \psi\cos \phi -\sin \psi\cos \theta \sin \phi & \cos \psi \sin \phi+\sin \psi\cos \theta\cos \phi & \sin \psi \sin \theta \\ -\sin \psi\cos \phi-\cos \psi \cos \theta \sin \phi & -\sin \psi \sin \phi+\cos \psi \cos \theta\cos \phi & \cos \psi \sin \theta \\ \sin \theta\sin \phi & -\sin \theta\cos \phi & \cos \theta \\ \end{array} \right) \end{equation}
ここで描いた回し方は「$z$軸→$x$軸→$z$軸」の順なので、「$zxz$のオイラー角」という言い方をする。これとは順番を変える定義もある。「$z$軸→$y$軸→$z$軸」の順にすると、$\theta,\phi$の意味が極座標の$\theta,\phi$に一致するのでこの順を使うこともある。また、「$x$→$y$→$z$」のように全部違う軸を使う方法もよく使われる。
ここで紹介したのと同じ回転を、操作の手順を少し変えて解釈して表すこともできる。こちらのたむぶんさんのページで説明されているので参考にしてください。
プログラムについて御質問、御要望、バグ報告などございましたら、前野［いろもの物理学者］昌弘へメールくださるか、または、twitterにてirobutsuまでメンションしてください。