位相空間とはなにか:はじめに
この文書は「よくわかる解析力学」【東京図書】の9.3節(215ページ)からの位相空間の概念について、動く図を使って説明したものです。
説明は1自由度の系で行う。よって、座標$q(t)$と、これに対応する運動量$p(t)$はそれぞれ1成分の量である。この、あわせて2次元となる$(q,p)$によって作られる空間を「位相空間」(phase space)と呼ぶ。
「相空間」と呼ぶ場合もある。数学用語で「位相空間」と訳される言葉として、もう一つ「topological space」があるが、これは全く別の概念。出てくる場面が重ならないので混同することはあまりないと思うが、誤解を避けたいなら「phase space(フェイズスペース)」と呼んだ方がよいかもしれない。
いろんな関数(ハミルトニアン等)を$q,p$の関数すなわち「$q,p$の1組を決めると値が決まる」量として扱う。よって$p$(本来、運動量であって座標ではない)を「位相空間内の点を表現する座標」と考えて、$H(q,p)$のような関数を「位相空間上の1点を定めると値が決まる関数」と考える。これに対し、座標$q$だけの空間は「配位空間」(configuration space)と呼ぶ($q$と速度$\dot q$の空間を「速度配位空間」と呼ぶこともある)。
以下でいろんな現象の場合の位相空間を動く図で見ていこう。
調和振動子の運動
配位空間・速度配位空間
下の図で表されるような、調和振動子の運動を考えよう。
最初から見たい時は、t=0に戻す。
質点●の運動を横軸x,縦軸tで表現したのが下のグラフである(通常と違って時間軸が縦になっているが、上の図と照らしあわせて見るためである)。これがいわゆる「配位空間」で、各時刻ごとの位置座標x(t)で運動を表現している。
スライダで振幅と角振動数を変化させることができるので、いろいろ変化させて運動の様子を確認して欲しい。
次に、速度を考えてみよう。
↓をクリックすることで、速度表示のOn/Offを切り替えられる。
右に(x,v)のグラフも出るので、運動の図と(x,t)のグラフ、(x,v)のグラフを見比べて、時間的変化がそれぞれの図でどのように表現されているかを見よう。
(x,v)の空間を「速度配位空間」と呼び、(x,p)の空間である「位相空間」とは少し違うのだが、この場合はp=mvであるから、縦軸をvでなくpにしても定数倍違うだけで、速度配位空間と位相空間は(この段階では)本質的違いはあまりない。次のページからは(x,p)のグラフで考えることにする(m=1にしておくので、グラフ自体は全く変化しない)。
あたりまえのことではあるが、ここで確認しておいて欲しいこと。
vが正である範囲(グラフの上半分)では、xは増加する。逆にvが負である範囲(グラフの下半分)では、xは減少する。
ここで考えているのは調和振動子なので、xが正である範囲(グラフの右半分)では、vが減少する(負の向きの力が働いている)。xが負である範囲(グラフの左半分)では、vが増加する(正の向きの力が働いている)。
位相空間での「運動」:自由粒子
位相空間(x,p)上で1点を指定すると、速度と初速度を指定しているのと同じであるから、その後の運動が全て決まる。
まず最も簡単な自由粒子の場合で、位相空間の1点に初期状態を与えるとその後どのような運動が起こるかを見てみよう。
←のグラフのどこかをクリックしてください。
上の(x,p)グラフのどこか一点をクリックするとその場所に質点●が現れ、その運動量を持って運動を開始する。
位相空間内の場所に従って、違う速度での運動が起こることを確認しよう。質点がグラフの外に出たら、またグラフのどこかをクリックするとまた質点が現れる。
運動量が0または非常に小さいところに置いてしまって、なかなか外に出ない場合は、次のボタンを押すこと。→消去
この状況を、位相空間内にpに比例した流れがあると解釈することもできる。自由粒子では、${\mathrm dx\over \mathrm dt}={p\over m},{\mathrm dp\over\mathrm dt}=0$だから、その流れは$\left({p\over m},0\right)$というベクトルになる。
上のグラフにその流れを表示させたかったら、↓のボタンを押してON/OFFの状態を切り替えよう。
位相空間での「運動」:重力場中
次に重力が働く場合を考えよう。ただし、この重力は左向き(x軸負の方向)に働くものとする。
↑のグラフのどこかをクリックしてください。
上の(x,p)グラフのどこか一点をクリックするとその場所に質点●が現れ、その運動量を持って運動を開始する。今度は重力が働くため、運動量は変化していく。
やはり、位相空間内の場所に従って、違う速度での運動が起こることを確認しよう。
質点を消したい時は、次のボタンを押すこと。→消去
この状況においては、${\mathrm dx\over \mathrm dt}={p\over m},{\mathrm dp\over\mathrm dt}=-mg$が成り立つから、位相空間の流れは$\left({p\over m},-mg\right)$というベクトルになる。重力加速度を変化させることもできるので、gの変化によりどのように運動および位相空間内での軌道が変化するかを見よう。
上のグラフにその流れおよびその流線(軌跡)を表示させたい場合、およびハミルトニアンの値を縦軸とした3Dグラフを表示させたい場合は、↓のボタンを押してON/OFFの状態を切り替えよう。
ただし、3D表示は機種・ブラウザによっては遅過ぎる場合もあるので注意。できるならwebGLに対応したブラウザで見て下さい。
特に3Dグラフを見ると、同じ高さのところ(つまりハミルトニアンが同じ値を取るところ)を動いていくことを確認しておこう。
まとめ
ここでは3つの運動(自由粒子、重力場中、調和振動子)について、位相空間内のどのような軌道に対応しているかを動く図で示した。
位相空間の中の流れは、
- 自由粒子$\left({p\over m},0\right)$、微分演算子で表現すると${p\over m}{\partial \over \partial x}$
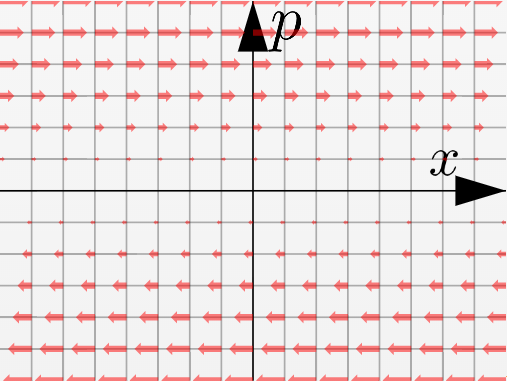
- 重力場中$\left({p\over m},-mg\right)$、微分演算子で表現すると${p\over m}{\partial \over \partial x}-mg{\partial \over \partial p}$
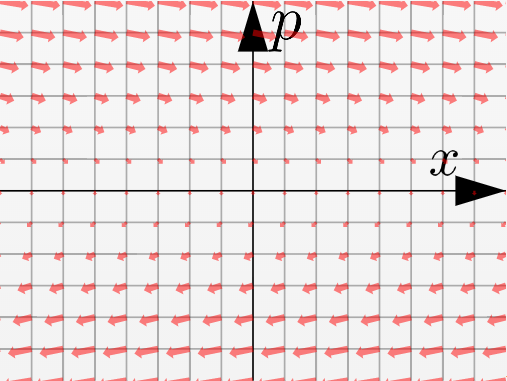
- 調和振動子$\left({p\over m},-kx\right)$、微分演算子で表現すると${p\over m}{\partial \over \partial x}-kx{\partial \over \partial p}$
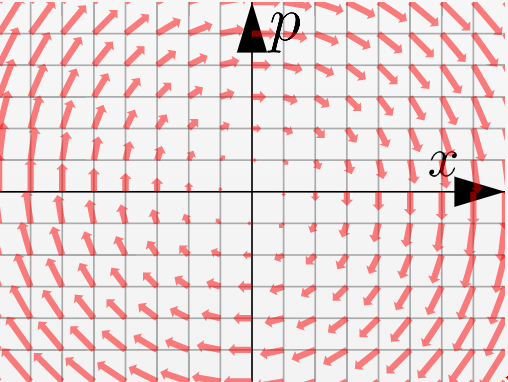
のようになっている。
実はこれらの「位相空間の流れ」ベクトルはそれぞれのハミルトニアン(自由粒子なら$H={p^2\over 2m}$、重力場中なら$H={p^2\over 2m}+mgx$、調和振動子なら$H={p^2\over2m}+{k\over2}x^2$)を使って、$\left({\partial H\over \partial p},-{\partial H\over \partial x}\right)$と書くこともできる。
このベクトル$\left({\partial H\over \partial p},-{\partial H\over \partial x}\right)$は、位相空間における$H$のgrad、つまり$\left({\partial H\over \partial x},{\partial H\over \partial p}\right)$と直交する。
${\rm grad}H$はハミルトニアンが変化する方向であるから、位相空間の流れがそれと直交しているということは、その流れに沿って(つまり運動方程式に従って)動いている限り、エネルギーは保存する、ということになる。


