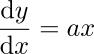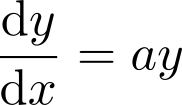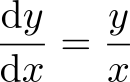微分方程式を図解する
はじめに
物理では(実は物理によらず、いろいろな場面では)「微分方程式を解く」必要があることが多い。なぜなら、物理法則のほとんどが「微分形」で書かれているからである。「微分形で書かれている」というのは「微小変化と微小変化の関係式で書かれている」と言ってもよい。物理の主な分野における基礎方程式は、運動方程式
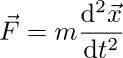
を初めとして、微分方程式だらけなのである。
微分方程式を解くには、積分という数学的技巧が必要になる。そのため「ややこしい」と嫌われる場合もあるようだ。
計算ではなく図形で「微分方程式を解いて関数を求める」というのはどういうことなのかを感じていただけたらと思い、アニメーションプログラムを作った。ただ計算するのではなく、「何を計算しているのか」をわかった上で計算のテクニックを学んだ方が理解は深まると思う。
ここでは微分方程式の中でも一番単純な「一階常微分方程式」を考える。「一階常微分方程式を解く」とはどういうことか、一言で言えば、
dxと dyの関係が与えられた時、xと y の関係を求める。
ということになる。
dxと dyの意味は、「xの微小な変化」と「yの微小な変化」である。

yはxの関数であるから、「xを一つ決めれば yが一つ決まる」という関係にある。そこで「xをほんの少し(dx)動かすとyはどれだけ(dy)動くか」という「変化と変化の関係」を考えることができる。関数が与えられた時にdyとdxの比(dy/dx)を計算するのが「微分する」もしくは「導関数を求める」という操作であった。
微分という操作の逆を行い、「各点各点におけるdyとdyの比」を与えて「じゃあ今考えている関数はどういう関数なのか」を決めるのが「微分方程式を解く」ということなのである。一般には
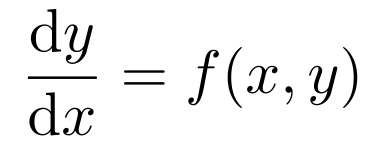
のように右辺はxとyの関数で書かれる。
では、次のページから、非常に簡単な例で微分方程式を図解していこう。
このページをandroidアプリ化したものが、
ここにあります。
目次
プログラムについて御質問、御要望、バグ報告などございましたら、前野[いろもの物理学者]昌弘へメールくださるか、または、twitterにてirobutsuまでメンションしてください。
1 一番簡単な例:(dy/dx)=a
一階微分方程式の中でも簡単とおもわれる、
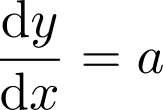 (aは定数)
(aは定数)
から始めよう。yという関数は微分したら定数aになる、というのだから、答はもう
y=ax+C (Cは積分定数)
となることはわかっているのだが、それをあえて図で表現してみたい。
図で考えると、(dy/dx)(すなわち、導関数または微係数)というのはつまり、「グラフの傾き」である。
a=1の場合を考えると、(dy/dx)=1つまり傾き1というのはx軸から45度の傾斜を持っている線だということになる。しかもこれは定数だから、どの点でも同じである。それを、次の図のように表す。
水平の黒線はx軸、鉛直の黒線はy軸である。
図の中の というマークは、(dy/dx)=1、つまり傾きが1であることを表現している。
というマークは、(dy/dx)=1、つまり傾きが1であることを表現している。
dyとdxが同じ、つまりxが変化する時、yも同じだけ変化しなさい、というのはx軸に対して45度の方向に動け、ということと同じなのである。
各場所で の方向に動けば、どのような線(関数)ができるか?---どうなるかを予想した上で
の方向に動けば、どのような線(関数)ができるか?---どうなるかを予想した上で
ボタンを押してみよう。
赤い線―で予想どおりの線が引かれたであろうか?
アニメーションを止めたい時は、
を押そう。
下のスライダで、
(dy/dx)=a
のa(つまり傾き)の値を(0〜3の範囲で)変えることができるので、その変化を観察しよう。
a=
2 少し方程式らしく:(dy/dx)=ax
少し問題を難しくして、
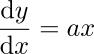
という微分方程式を考えよう。この場合の(dy/dx)を表す図は、
である。つまり、傾きがxの1次式で変化する(右へ行くほど傾きが急になることを確認しよう)。y軸より左では傾きがマイナスなので、右下がりの傾きになっている。
では、各場所でこの傾きにしたがって線を引いていくとどうなるか?
予想した後で、
ボタンを押してみよう。
赤い線―で予想どおりの線が引かれたであろうか?(この線の形が予想できただろうか?)
アニメーションを止めたい時は、
を押そう。
下のスライダで、(dy/dx)=aのaの値を(0.1〜3の範囲で)変えることができるので、その変化を観察しよう。
a=
計算により微分方程式を解く場合、この式は
(dy/dx)=ax
y= ax^2/2 +C
のように解かれる。
3 では次は:(dy/dx)=ay
今度は
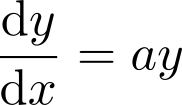
を考えてみよう。この式は「yが大きいほど傾きが大きくなる」を意味している。図を見て傾きがy座標に比例していることを確認した後、前頁までと同様にグラフを書かせてみよう。
以下のボタン類の意味はこれまでと同様。
a=
計算で答を出すのであれば、
(dy/dx)=ay
y= C exp(ax)
となる。グラフが指数関数であることを確認しよう。
4 (dy/dx)=y/x
今度は
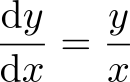
を考えてみよう。
この式の意味するところは「グラフの傾き(下の図の水色の直角三角形の斜辺の傾き)と(y/x)(下の図の青色の直角三角形の斜辺の傾き)が等しい」である。
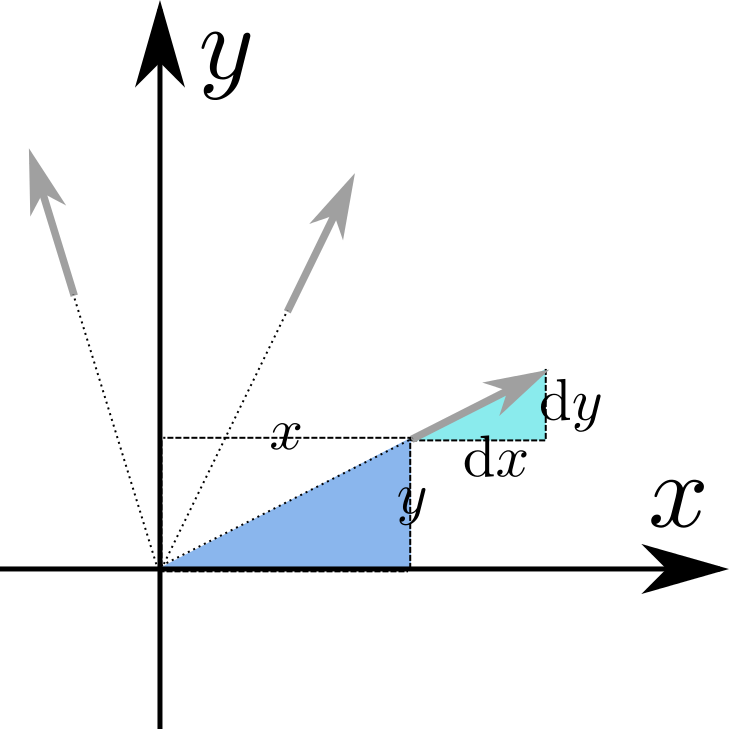
この下にこれまで同様の「動く図」がある。どのような関数になるか、だいたいわかると思うが、これまで同様に絵を書かせてみよう。
以下のボタン類の意味はこれまでと同様(このページでは、aは変えられない)。
計算で答を出すのであれば、
(dy/dx)=y/x
から(ちょこちょこと計算することで)
y= C x
となる(この場合図で考えるより計算する方がむしろ難しい!)。
これが
(dy/dx)=ay/x
だとどうなるかもやってみるといいだろう。次に用意した最後のページでいろんな場合を試すことができる。
最後のページ:いろいろやってみよう
さて、最後のページではいろんな関数を表示できるようにしてあるので、自由に遊んでみて欲しい。
ゆっくりとアニメーションで図を書くのがまっていられない人の為に、一挙に線を引いてしまうこともできるようにした。下にある「描画モード」を選べばよい。
微分方程式を計算して解いていくのはもちろん大事だが、こういう図のイメージで「微分方程式を解いて関数を求める」というのは何をやっているのかを感じておくのも大事である。
a=
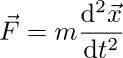

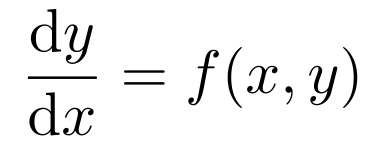
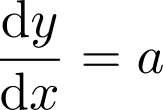 (aは定数)
(aは定数)