調和振動子の波動関数
調和振動子の波動関数をアニメーションで書きます。たとえばn=0のスライダだけを動かして0でなくすると、
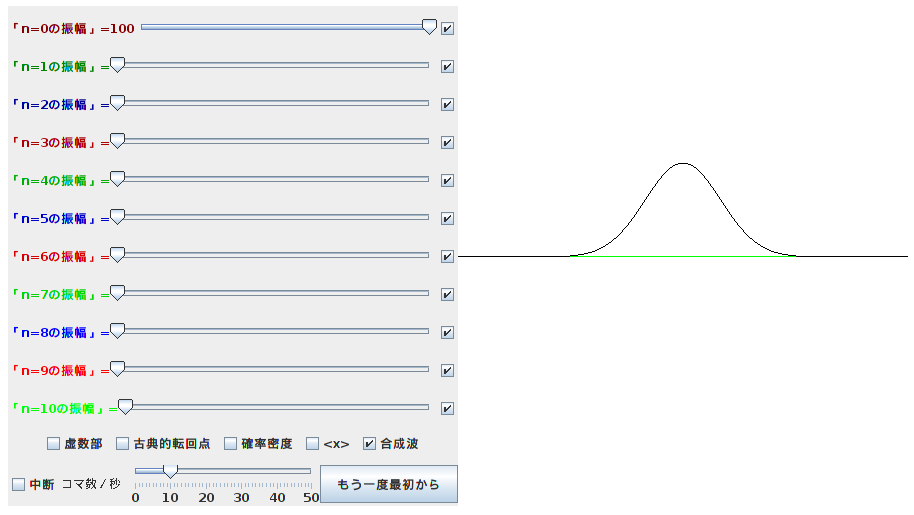
のような基底状態の波動関数が動いているところが見えます。
n=1の振幅だけを0でなくすると、
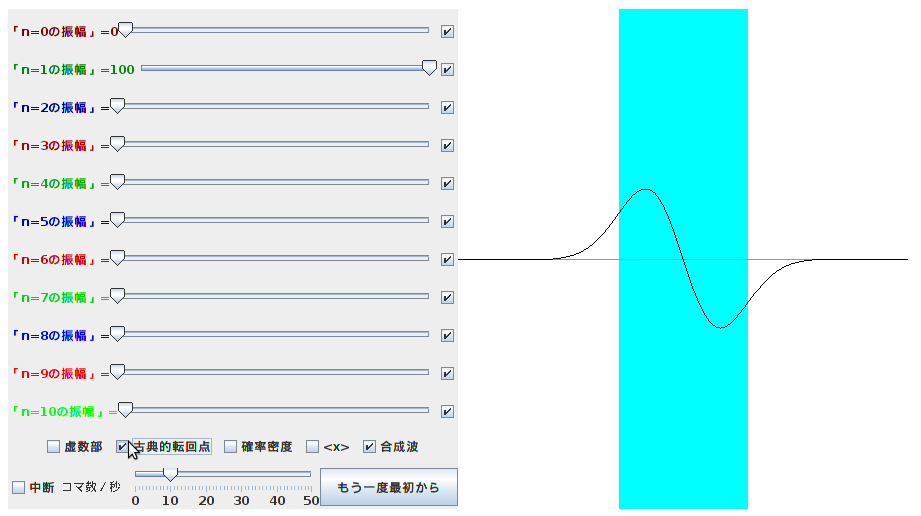
↑の図では、「古典的転回点」を表示させています。具体的には↑の図の中の水色の領域で、古典的に許されるのはこの範囲の運動です。この外では波動関数が減衰していることに注意してください。
「古典的転回点」は、エネルギー固有状態でのみ定義されるものなので、モードのうち一つだけがnon-zeroになっている時しか意味がありません。
n=0とn=1を合成した波動関数の様子が
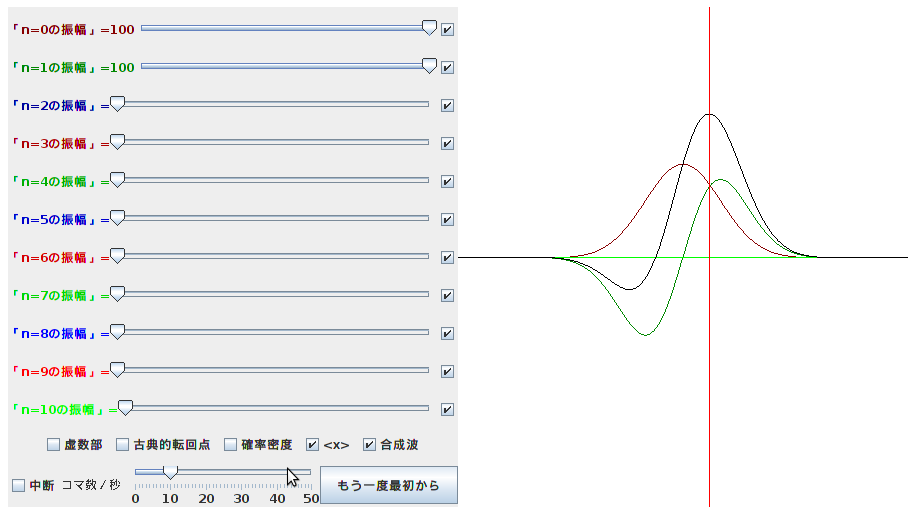
です。二つの波動関数がどのように重なっているかを確認しましょう。この場合<x>というところにチェックをいれていますが、こうしているとxの期待値が赤い線で表示されます。ちゃんと左右に揺れることを確認しましょう。
もっと複雑な足し算をすると、
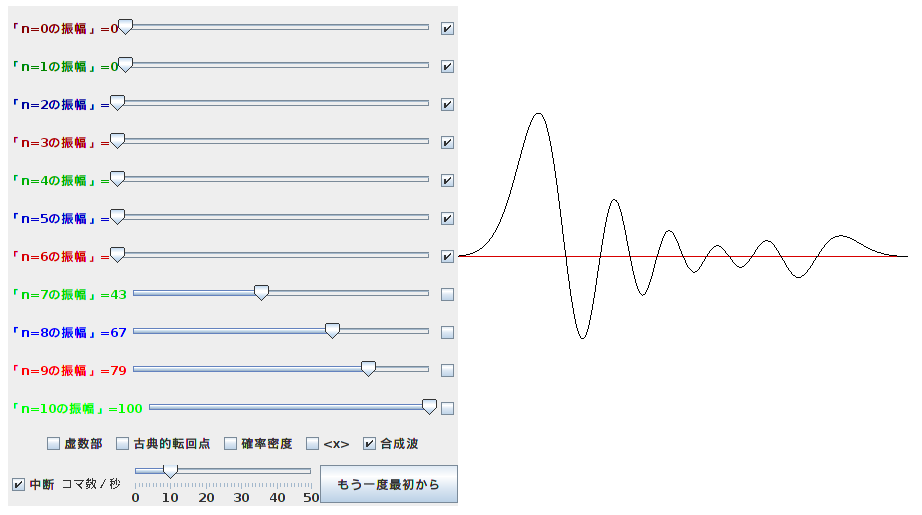
のような「振り子がいったりきたりする様子」に対応する波動関数を見ることができます。
確率密度や波動関数の虚数部を表示させるチェックもついてます。