ファンデルワールスの状態方程式
下に「動くグラフ」があるので、いろいろな場合で温度を変化させて、
- ある「臨界温度」より高いとき、グラフは単調減少になること。
- 臨界温度より低いときは、同じ圧力に対して体積が三つ存在することがあること。
を確認しよう。
青い線はヘルムホルツ自由エネルギーのグラフである。やはり、
- 臨界温度より高いとグラフは常に下に凸。
- 臨界温度より低いときは、グラフに下に凸でない領域が出現する。
ことを確認しよう。
a[10-3Pa・m6・mol-2]
b[10-6m3・mol-1]:
T[K]:
体積（横軸）は1目盛が
圧力（縦軸）は1目盛が
ヘルムホルツ自由エネルギー（縦軸）は1目盛が
初期値であるa=141、b=39は窒素の場合の値。
たとえば水蒸気（水）の場合でどうなるか、などを見てみよう。
下の図の赤く塗った部分では、圧力すなわち$-{\partial F\over\partial V}$が一定のままで体積が変化する。これが「気相・液相の共存領域」になる。
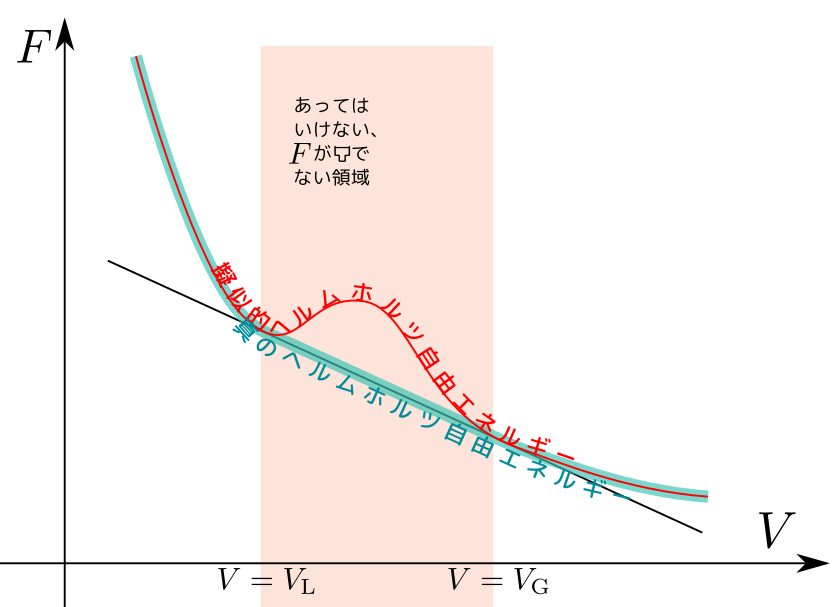
上の「動くグラフ」でも温度に応じて（低温のときに）このような領域が現れることを確認しよう。
この共存領域をV-Pのグラフ上に表現すると↓のようになる。
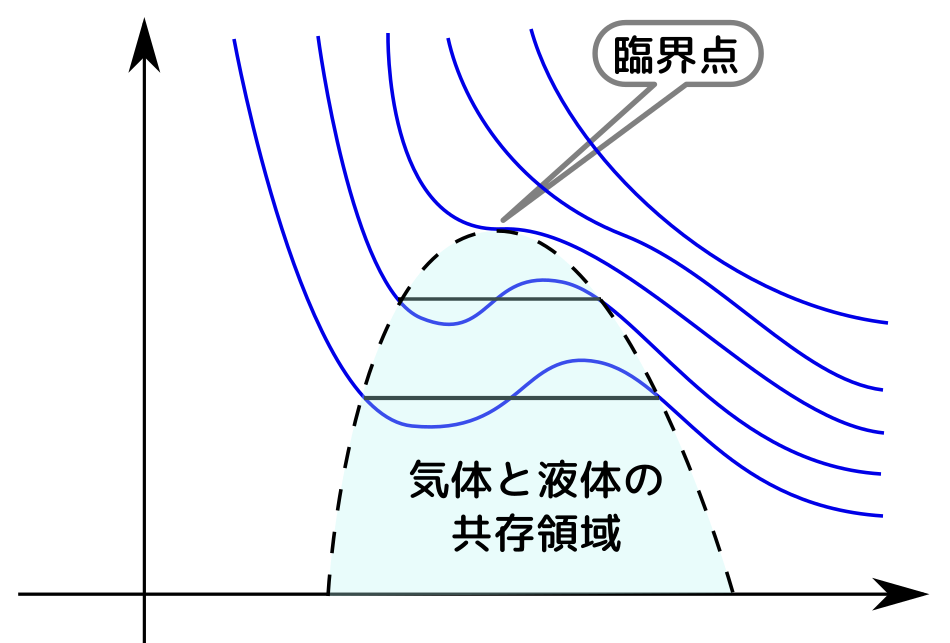
この間に、たとえば液体→気体と相転移したなら、ぐっと体積が増える（液体窒素→気体窒素の場合で700倍）。