ステイホーム勉強問題集

　このページは、谷村省吾さんの呼びかけ

に賛同して作った「物理のステイホーム勉強」問題集です。

　ときどき学生さんとかに出している問題を出してみます。レベルも対象もいろいろですが、楽しんでみてください。

　解答はGW終了の頃にまとめてアップロードすることにしようと思っています。基本、それまでは解答やヒントは出さないで自由に楽しんでもらうというつもりでおります（ヒント出してしまうと自明な問題になっちゃう場合もあるので）。問題の意図がわからん、みたいなコメントもありましたので、補足を入れておきますので、疑問に思うことなどある人は該当部分をクリックしてください。

問題集

磁場中の電子のボーア・ゾンマーフェルト条件とランダウ準位

2020.5.16追加↓　解答は一週間後ぐらいに。

2020.5.22追加↓

　解答はこちらにあります。

ロケットの加速の有利不利

2020.5.5追加↓

　解答はこちらにあります。

Heisenberg方程式と$\hat H=\mathrm i\hbar{\partial \over\partial t}$

この人がどう間違えて(1.2)を出したのかよくわからない、という人はこの文章をクリックすると説明が出現します。 この人は、「だって、右辺に、$\hat H=\mathrm i\hbar{\partial\over\partial t}$を代入したら、 $$\left[\hat A(t),\mathrm i\hbar{\partial\over\partial t }\right]=\mathrm i\hbar\left(\hat A(t){\partial\over \partial t}-{\partial\over \partial t} \hat A(t)\right)=-\mathrm i \hbar {\mathrm d\over\mathrm dt}\hat A(t)$$ じゃん！」と考えました。この考えはどこが間違っているかを説明してあげてください。

2020.5.6追加↓

　解答はこちらにあります。

超伝導リングと永久機関？

2020.5.6追加↓

　解答はこちらにあります。

ロケットの加速の有利不利

　状況をもう少し詳しく図にすると下の通り。

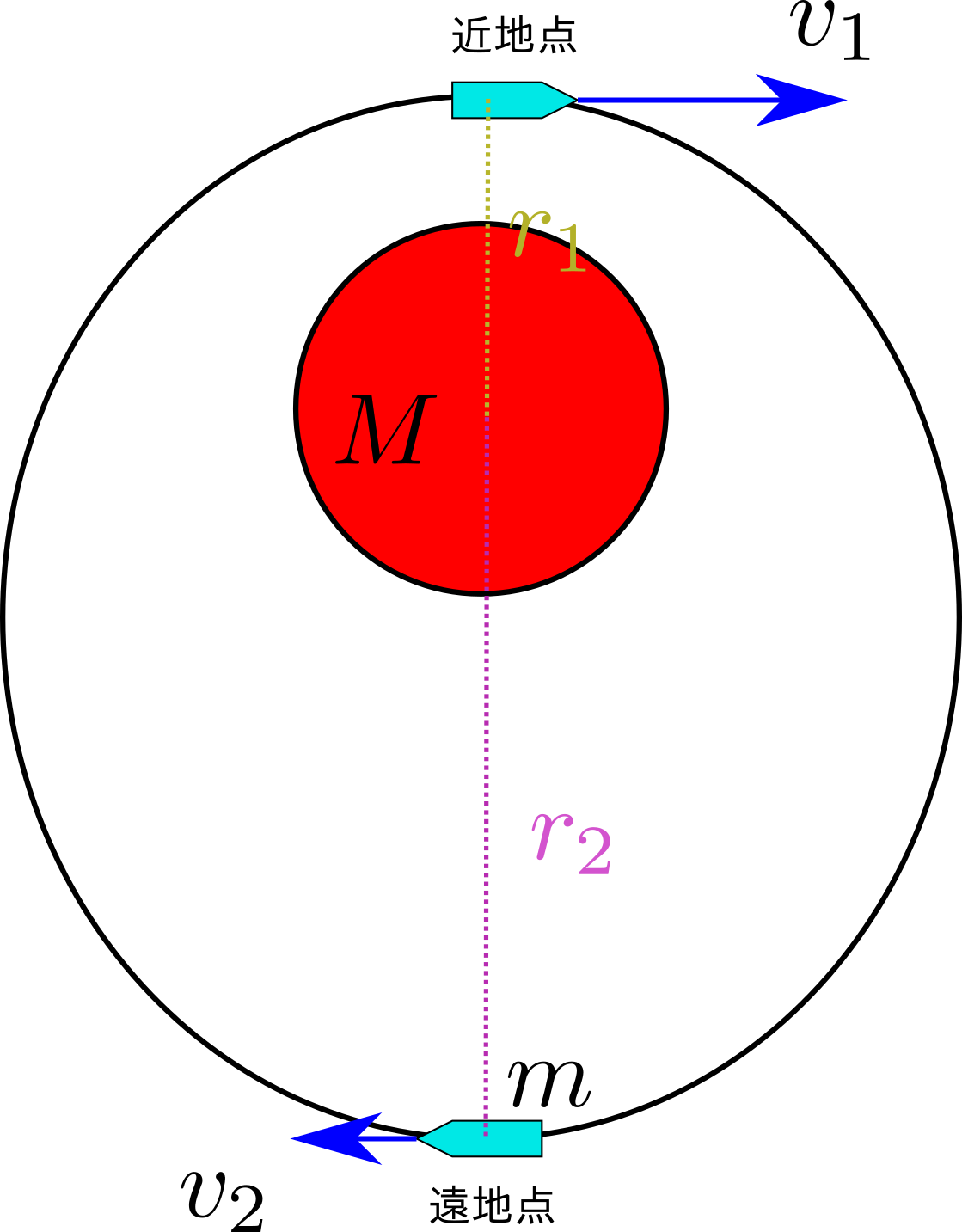
　画像を見てまず気づくことは

  1. 近地点での速さは遠地点での速さより大きい（$v_1> v_2$）
  2. 近地点での位置エネルギーが遠地点での位置エネルギーより小さい（$-{GMm\over r_1}<-{GMm\over r_2}$）

ということだろう。

　ここで考えているのは「加速したときの力学的エネルギーの変化」だが、この加速の間に位置は大きくは変化しないとすれば、2.の効果は関係なさそうだ。

　この「加速」によって、速さが$\Delta v$だけ増えるとしよう。すると、近地点での運動エネルギーの増加は $${1\over2}m(v_1+\Delta v)^2 - {1\over2}m(v_1)^2 = m v_1\Delta v + {1\over2}m(\Delta v)^2$$ となる。同様に計算すると遠地点では $${1\over2}m(v_2+\Delta v)^2 - {1\over2}m(v_2)^2 = m v_2\Delta v + {1\over2}m(\Delta v)^2$$ だけエネルギーが増加する。

　比較すると、エネルギーの増加は近地点の方が多い（$m v_1\Delta v>m v_2\Delta v$だから）と気づく。

　これでなんだそんだけのことかで終わってしまうと、問題の同じ燃料を消費するのだから同じかと思いきや、差が出るのはなぜ？？の部分に答えきれていない。この問いをした人は

同じ燃料を消費している（つまり燃料の持っている化学的エネルギー原子力ロケットなら核エネルギーだがは同じだけ使っている）のに、ロケットの得るエネルギーが違うのはなぜ？

ということに疑問を感じているのである。だから、上の式を見せて元々の運動エネルギーが大きい方がエネルギー増加も大きいねっ！だけで終わったら、きっと不満だろう。

　ここまで読んで「おっと、上のところまで考えてなかった」という人は、もう一度考えてから、下のボタンを押して続きを読もう。ちゃんとその先まで考えたよ、という人はすぐに続きに進もう。
ロケットの加速の有利不利（続き）

ロケットの加速の有利不利（続き）

　さて、

同じ燃料を消費している（つまり燃料の持っている化学的エネルギーは同じだけ使っている）のに、ロケットの得るエネルギーが違うのはなぜ？

という疑問に答える方法は二つある。

  1. エネルギーの増加は「仕事」であることを使う。
  2. ロケット以外の物体のエネルギーをちゃんと考える。

エネルギーの増加＝仕事

　まず1.から。仕事は（力）×（力の方向への移動距離）である。同じ燃料を使っているのだから、近地点でも遠地点でも、同じ大きさ$F$の力を同じ時間$\Delta t$だけロケットに加えることができたとしよう。つまり、力積の大きさ$F\Delta t$は、どちらも同じである。

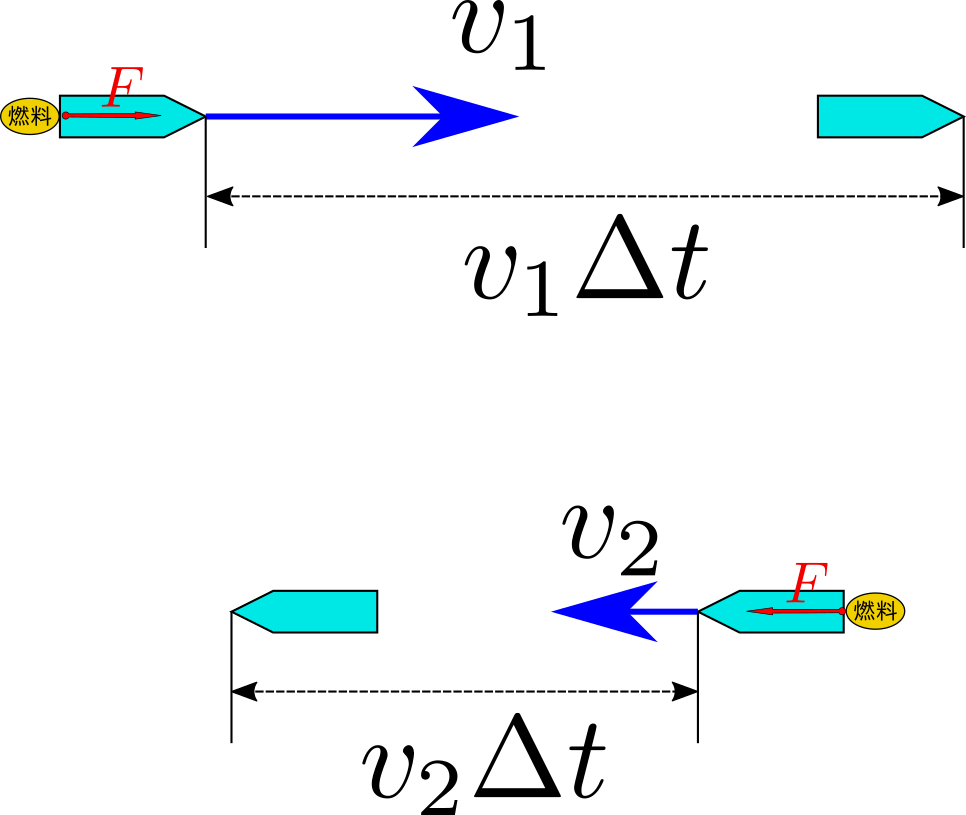
　この間にロケットが進む距離は概ね$v_1\Delta t$（近地点で）と$v_2\Delta t$（遠地点で）であるもう少しちゃんと計算しても面白いが、ここでは「概ね」で済ませておこう。である。

　上のように移動を考えると、ロケットにされる仕事は、

となる。近地点の方が大きい。つまり「同じ力を加えられても、その間に動く距離が長ければ仕事は大きくなる」ということなのである。

　力積の大きさが同じでも、仕事の大きさが同じとは限らないというのが、エネルギーの変化（仕事で決まる）が同じにならない理由である、と言える。

　「エネルギー増加の大小を知りたければ、仕事を見よ！」というのがこの解答の教訓である。

　とはいえ、「エネルギーは保存するはず」という感覚を持っていると、この説明でもまだ「？」が残る人はいるだろう。というわけで、もう一つの「ロケットが得るエネルギーが同じではない理由」を考えよう。

ロケット以外の物体のエネルギー

と聞いて「地球のエネルギーか？」と思った人もいるかもしれないが、さすがにここで地球は関係ない。もう一人の登場人物は「燃料」である。

　噴射前と噴射後の、ロケットと燃料の運動を見ると（これも「概ね」の計算だが）、

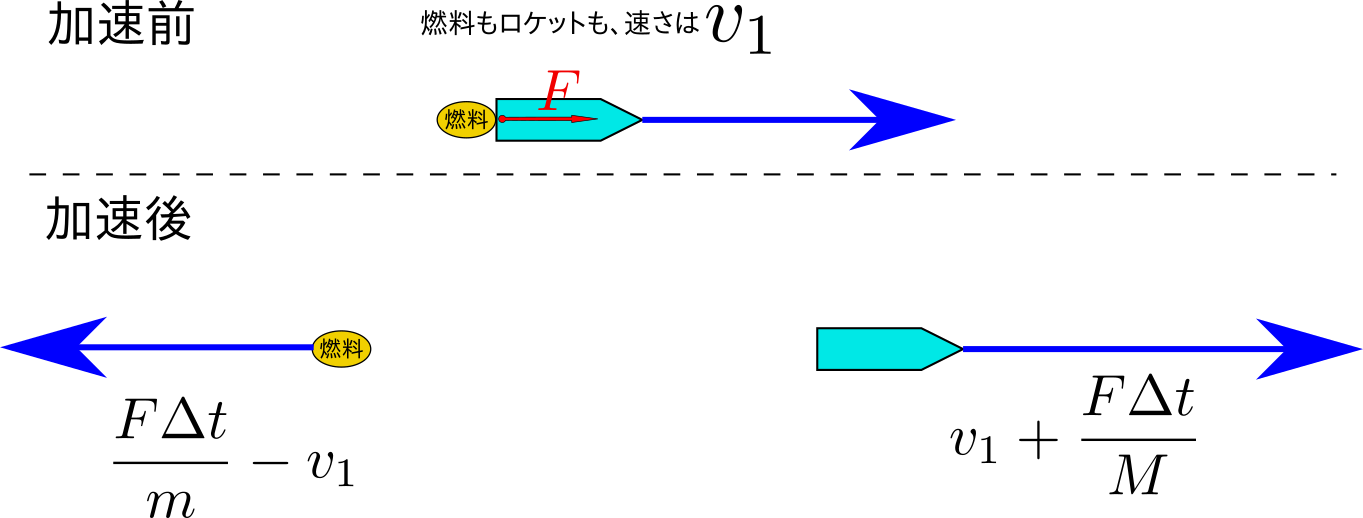
のようになる。$F\Delta t$という力積をロケットと燃料が互いに与え合うので、最初どちらも速さ$v_1$だったロケットと燃料の速さは、$v_1-{F\Delta t\over M}$と$\left|{F\Delta t\over m}-v_1\right|$に変わる上の図では、${F\Delta t\over m}-v_1>0$の場合で書いている。のである。

　このとき、加速後の全エネルギーを計算してみよう。 まず燃料の運動エネルギーは${1\over 2}m\left({F\Delta t\over m}-v_1\right)^2$、ロケットの運動エネルギーは${1\over2}M\left(v_1-{F\Delta t\over M}\right)^2$である。この二つの和は $${1\over2}{\left(F\Delta t\right)^2\over m}-F\Delta t v_1 + {1\over2}m(v_1)^2+{1\over2}{\left(F\Delta t\right)^2\over M}+F\Delta t v_1 +{1\over2}M(v_1)^2$$ となるが、$F\Delta t v_1$が$\pm$の符号を持って２回出てくるので消しあい、結果は $${1\over2}\left({1\over m}+{1\over M}\right){\left(F\Delta t\right)^2\over m}+{1\over2}(M+m)(v_1)^2$$ となる。第２項の${1\over2}(M+m)(v_1)^2$が最初のエネルギーであることから、第１項の${1\over2}\left({1\over m}+{1\over M}\right){\left(F\Delta t\right)^2\over m}$が「全力学的エネルギーの増加」であり、これは$v_1$には依らない（つまりこれが燃料が消費したエネルギーなのだ！）。

　この燃料が消費したエネルギーはロケットと燃料に分配されるから、燃料の取り分を減らせばロケットの取り分は増える（ロケットはより大きな力学的エネルギーを得ることができる）。

　燃料が獲得する力学的エネルギーは上の計算から、${1\over2}{\left(F\Delta t\right)^2\over m}-F\Delta t v_1$だから、$v_1$が大きいほど小さくなる。

　こうして、近地点で加速した場合（というより、初速度が大きい状態から加速した場合）の方が、燃料が最後に持っている運動エネルギーが少ない（その分、ロケットの持つ運動エネルギーが多くなる）のである。

「ロケットが加速する」という問題だからといって、ロケットの運動エネルギーだけを見ていたのではいか〜〜んん！！---というのがこの問題の教訓である。

ロケットの加速の有利不利

Heisenberg方程式と$\hat H=\mathrm i\hbar{\partial \over\partial t}$

　まず身も蓋もないことを先に言ってしまえば、$\mathrm i\hbar{\partial\over\partial t}=\hat H$が成立するのは、

ときである。つまり、

$\mathrm i\hbar{\partial\over\partial t}\left|\Psi(t)\right>=\hat H\left|\Psi(t)\right>$は成り立つがだからといって$\mathrm i\hbar{\partial\over\partial t}=\hat H$とは限らない。

のである。

　問題の式の右辺の右から、$\left|\Psi(t)\right>$を掛けてみたとしよう$\hat A(t)$はHeisenberg表示、$\left|\Psi(t)\right>$はSchrödinger表示なので、「混ぜるな危険」であるが、どうせ間違った計算なので危険を承知で計算する。。すると、 $$\begin{array}{rl} \left[\hat A(t),\hat H\right]\left|\Psi(t)\right>=& \left(\hat A(t)\hat H-\hat H \hat A(t)\right)\left|\Psi(t)\right> =\hat A(t)\hat H\left|\Psi(t)\right>-\hat H \hat A(t)\left|\Psi(t)\right> \\ \end{array}$$ となるが、第１項を$\hat A(t)\hat H\left|\Psi(t)\right>=\hat A(t)\left(\mathrm i\hbar{\partial\over\partial t}\left|\Psi(t)\right>\right)$と書き直すのはいい。だが、第２項を$\hat H \hat A(t)\left|\Psi(t)\right>=\mathrm i\hbar{\partial\over\partial t}\left(\hat A(t)\left|\Psi(t)\right>\right)$としてはいけない。$\hat A(t)\left|\Psi(t)\right>$はSchrödinger方程式の解ではないからである。

実はこの後「じゃあどうして正解は間違えた計算のちょうど反対符号なのか」を書こうとしたのだが、やってみると結局Heisenberg方程式をもう一回導出するのと同じ計算になっていることに気づいたので、やめておく。

超伝導リングと永久機関

　twitterでの反応を見ていると、これが一番正解が多かったように思う。

　正解を書くために、Maxwell方程式を復習しよう。 $${\rm div}\vec D=\rho,~~{\rm div}\vec B=0,~~{\rm rot}\vec E=-{\partial\vec B\over\partial t},~~{\rm rot}\vec H=\vec j +{\partial\vec D\over\partial t}$$ である。だがこれはモノポールなんてものがない場合の式なので、ある場合は

$${\rm div}\vec D=\rho,~~{\rm div}\vec B=\color{red}{\rho_M},~~{\rm rot}\vec E=\color{red}{-\vec j_M}-{\partial\vec B\over\partial t},~~{\rm rot}\vec H=\vec j +{\partial\vec D\over\partial t}$$ と変更しなくてはいけない（磁極密度$\rho_M$と磁流密度$\vec j_{\rm M}$が加わる）。ここで、磁流密度は電流密度とは逆符号で加わることに注意しよう（${\partial \vec D\over\partial t}$と${\partial \vec B\over\partial t}$と同様だ）。

　これは「電流が作る磁場」が「右ねじの法則」を満たしたのに対し、「磁流の作る電場」は「左ねじの法則」を満たすことを意味する。

　というわけでモノポールが動くことによってできる電場を図に描き足すと、

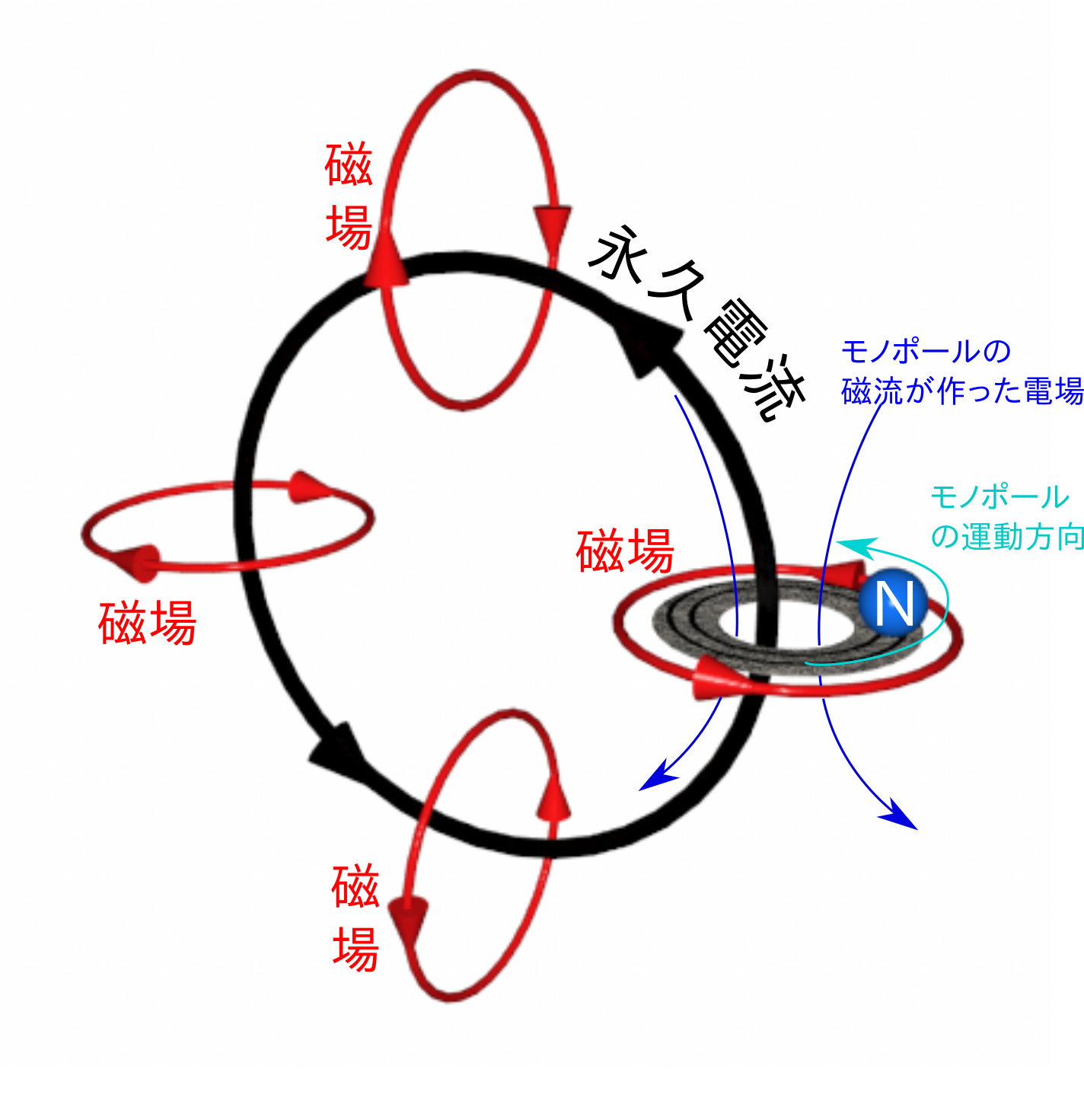
となる。この「磁流が作った電場」は超伝導体を流れる電流と逆向きであり、電流を弱くする効果がある（つまり永久電流でなくなるのだ）。

　つまり、モノポールの円運動によって作られた電場が電流を小さくしていき、電流が0になったところで止まる。

　こうなったのは「磁流の作る電場」は「左ねじの法則」になるからで、それは元はと言えば、Maxwell方程式のDとBの時間微分の項が逆符号であることが効いている。

磁場中の電子のボーア・ゾンマーフェルト条件とランダウ準位

　量子力学の問題だから量子力学の方に何か間違いがあるのでは、と思った人も多かったかもしれない。しかし、実は古典力学的な部分ですでに間違えているのである。

　間違いは、ボーア・ゾンマーフェルトの量子化条件$\oint p\mathrm dq$の$p$に$mv$を代入してしまったことである。

　磁場中（というよりはベクトルポテンシャルがある空間中）の運動量は$\vec p=\vec mv$ではなく、$\vec p=m\vec v+q\vec A$なのである。電子の電荷が$-e$であることを考えると、$\vec p=m\vec v -e\vec A$という式を使わなくてはいけない。つまり量子化条件は $$\oint(m\vec v-e\vec A)\cdot \mathrm d\vec q=nh$$ になる。この第２項の$-e\oint\vec A\cdot \mathrm d\vec q$を考えよう。

　ストークスの定理を使うと、 $$\oint \vec A\cdot \mathrm d\vec q= \int\left({\rm rot}\vec A\right)\cdot \mathrm d\vec S$$ が成り立つ。${\rm rot}\vec A=\vec B$だから、この積分$\int\vec B\cdot \mathrm d\vec S$は電子の円軌道を貫く磁束であり、つまりは答えは$\pi r^2 B$となる。よって量子化条件は $$ mv\times 2\pi r -e \pi r^2 B=nh $$ になるのである。

　さて、電子の運動方程式は（等速円運動なので） $${mv^2\over r}=evB$$ であり、これから$mv=eBr$がわかる。ゆえに、量子化条件は $$ mv\times 2\pi r - \overbrace{\pi r\times mv}^{e\pi r^2B}=nh $$ となり、 $$ \pi r mv = nh $$ と、$-e\vec A$を忘れていたときの計算の半分になる。$r={v\over\omega}$を使いつつ、これからエネルギーを計算すると、 $$ {1\over 2}mv^2 = {nh\omega\over2\pi} $$ となって、ランダウ準位と同じ式となる。

　なお「磁場のエネルギーを入れるべきなのでは？」と思った人ももしかしたらいるかもしれないが、磁場からの力は、常に運動方向と垂直に働く力なのでエネルギーに寄与しない（これも古典力学からそう）。

　実は、一様磁場中を円運動する荷電粒子が調和振動子と等価な力学系であることは（ハミルトニアンが正準変換で一致するという意味で）古典力学だけでわかることなのである。

　なお、この場合、量子力学において$-\mathrm i\hbar{\partial\over\partial x}$に置き換えられるのはもちろん、$mv$ではなく、$mv+qA$である。