運動方程式
\begin{equation}
m\left({\mathrm d\over\mathrm dt}\right)^2 {x}= -K{\mathrm d\over\mathrm dt}{x}-k{x}
\end{equation}
から、例によって特性方程式を作ると、$m\lambda^2 +K\lambda +k=0$となる。これの解は(二次方程式の解の公式を用いて)
\begin{equation}
\lambda_\pm={-K\pm\sqrt{K^2-4mk}\over 2m}=-{K\over 2m}\mp{{\sqrt{K^2-4mk}}\over 2m}
\end{equation}
となる。ここから、$K^2-4mk$が負の場合、0の場合、正の場合の三つに分けて考える。
このように「場合分け」をしなければいけないというのが、運動に種類がある(予想では2種類だったが実は3種類だった)理由である。
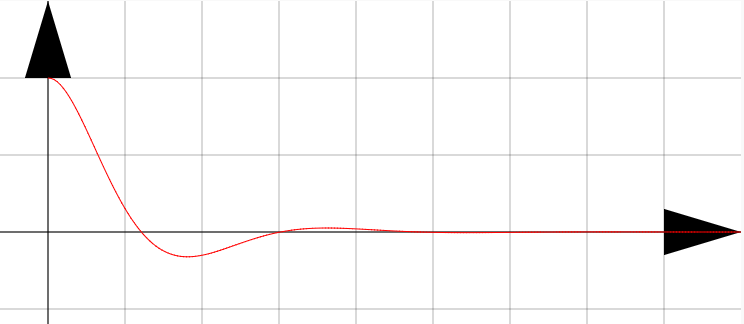
$K^2-4mk<0$の場合この場合は$\lambda$は複素数になる。$\omega={\sqrt{4mk-K^2}\over 2m}$という定数($\omega$は実数である)を定義し、 $\lambda_\pm=-{K\over 2m}\mp\mathrm i\omega$と書くことにする。
こうして解を
\begin{equation}
{x}=
C_+ \mathrm e^{-{K\over 2m}{t}+\mathrm i\omega{t}}
+C_- \mathrm e^{-{K\over 2m}{t}-\mathrm i\omega{t}}
\end{equation}
と表すことができる。一見複素数であるが例によって係数を操作して、$C_+=C,C_-=C^*$とすることで
\begin{equation}
{x}=
\mathrm e^{-{K\over 2m}{t}}\left(
C\mathrm e^{\mathrm i\omega{t}}
+C^* \mathrm e^{-\mathrm i\omega{t}}\right)
\end{equation}
が実数解となる。
つまり、この式をちゃんと計算すると、実は虚数$\mathrm i$はどこにもいないのだ!
そのことを確認するために、$C=A+\mathrm iB,C^*=A-\mathrm iB$などと置いて計算をしてみる。
オイラーの公式$\mathrm e^{\mathrm i\theta}=\cos\theta+\mathrm i\sin\theta$などを使って、結果を三角関数で表現すると以下のようになる($A,B,D,\alpha$は実数の定数)。
\begin{equation}
{x}=2
\mathrm e^{-{K\over 2m}{t}}\left(
A\cos \omega{t}
+B\sin\omega{t}\right)
=
D\mathrm e^{-{K\over 2m}{t}}
\cos \left(
\omega{t}+\alpha\right)
\end{equation}
下の動くグラフに$K^2-4mk<0$になる値(ちなみに$m=1$で固定であるから、$K^2<4k$ということ)を代入してみよう。二つの解(青と赤)がプロットされる。線形結合を取ることでいろんな解が出ることもわかる。
$K^2-4mk=0$の場合この場合、$\lambda_+=\lambda_-$となる。よって添字は取って、$\lambda=-{K\over 2m}$と書こう。重解が出る場合であるから、解は以下の通り。
\begin{equation}
{x}=\left(C_1{t}+C_0\right)\mathrm e^{\lambda{t}}
\end{equation}
この解「臨界振動」は、$K^2-4mk<0$と$K^2-4mk>0$のちょうど境目にあたる。
下の動くグラフに$K^2-4mk=0$になる値($K^2=4k$ということ)を代入してみよう。
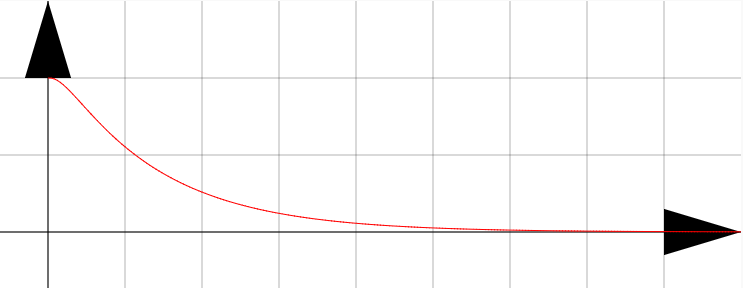
$K^2-4mk>0$の場合この場合は単純に、
\begin{equation}
{x}=
C_+ \mathrm e^{\lambda_+{t}}
+C_- \mathrm e^{\lambda_-{t}}
\end{equation}
が解である。$\lambda_\pm$はどちらも負の数になるから、この二つの解のどちらも「指数関数的に減衰する解」である。
これも下のグラフにいろんな数値を入れてみよう。
A=1
B=1
K=1
k=1