準静的操作（等温操作）

　では力学の復習をしながら、

エネルギーは仕事が行われるとその仕事の量だけ増減（仕事をした方はエネルギーが$W$減少、された方はエネルギーが$W$だけ上昇）する物理量である。

というような話をした。

　熱力学では、この仕事とエネルギーの考え方を（熱力学で扱う状況に合わせて）変化させていかなくてはいけないそして、仕事以外のエネルギー移動の形態として「熱」というものを登場させていくことになる。。

　まず、等温変化における仕事について考えよう。

　理想気体の状態方程式$PV=NRT$を満たすような気体を考えよう。

　断面積$S$のシリンダーに閉じ込められた圧力$P$の気体を考えると、気体がピストン（やはり断面積$S$を押す力は$PS$だから、ピストンが$\Delta x$動いて気体が膨張したときの仕事は$PS\Delta x=P\Delta V$と書くことができる。$P$は変数だから、仕事は$\int P\mathrm dV$であり、$P={NRT\over V}$で、かつずっと等温のままで変化が起こるとすれば、仕事は \begin{equation} \begin{array}{rl} W=&NRT\int{\mathrm dV\over V}\\ =&NRT\left[\log V\right] \end{array} \end{equation} となる。

というのはいくつかの仮定を置いた計算としてそうなるのだが、現実はそれとは少しずれが生じる。

上のような計算は初等力学で言えば摩擦はないとして空気抵抗を無視するとに対応する、「理想的」計算なのである。熱力学の場合でも「現実に起こる変化」と「理想」の間には隔たりがある。以下で、より現実的な話と、その現実を「理想化」したものである準静的操作などについて話していこう。
　熱力学を考えるうえでとても重要な概念が「準静的操作」である。準静的操作は一つの理想的状況であって、現実には存在しない。
　現実には存在しないのではあるが、それを使うことで、熱力学における「状態変化」が記述できる。

　というわけで現実には存在しない準静的操作であるが、では現実とはどのように違うのだろうか。そこで、（まだ現実ではないんだけど）「準静的操作よりは現実に近い状況のシミュレーション」を見せよう。

　下の図で、ピストンを押したり引いたりしてみよう。画像の色は温度を表す（赤が高温、水色が低温である）。

　色の透明度が圧力を表しているので、濃い色のところほど圧力が高いと思ってよい（真っ白な部分は真空に近い）。ピストに働いている力（圧力）は矢印で表現している。

　押したり引いたりすることで、気体は圧縮され温度が上がったり膨張して温度が下がったりしつつ、圧力や体積が変化していく。ピストンの移動は矢印で表現している。

　このシリンダーは、左端だけは断熱されておらず、左端に接した部分の気体は温度が一定である壁に接している（↓の図では、左端が黒ではないことで「左端からは熱が出入りする」ことを表現している）。

　

　プログラムの都合上、あまり急速にピストンを押されると（体積が圧縮されすぎて負になったりして）おかしなことが起こるので、ボタンを押したらじわっと動くようになっている。速度は真ん中にある速くなどと書いてある部分をクリックすることで変えられる。

　左端の部分は温度一定の壁に接しているので等温に保たれる。そして、時間が経過すれば全体が等温に達する（平衡状態）。左端からだけ熱が出入りするようにしたのは、プログラムの都合（1次元的な現象にしたかった）であって物理的意味はない。

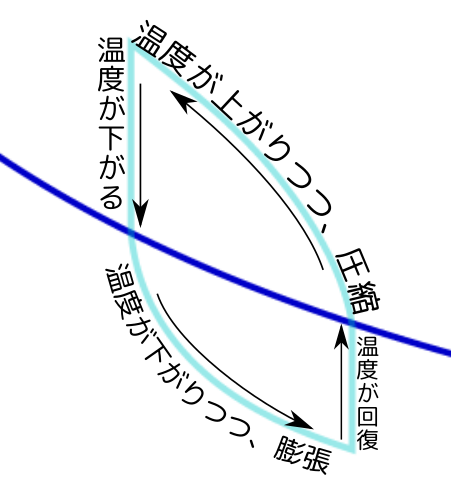
　さて、ピストンを引いてみると、引かれた部分は気体を膨張させたことになるので、圧力が下がり温度も下がる。

↑この絵は単なる画像です。動きません。

　「等温操作」という名前ではあるがこのように操作を行なうと、操作の間じゅうずっと等温というわけにはいかない。↑の図のように、ピストンに近い部分は温度が下がり、シリンダーの気体内に温度勾配ができる。

　そして、その変化が二つの理由で伝わる。二つの理由とは、

  1. 膨張して気圧が下がったので、隣の気体がこちらに移動してくる（いわば、「高気圧から低気圧へ風が吹く」）
  2. ピストン付近の気体の温度が下がったので、隣の気体（まだ温度が下がってない）から熱が移動してきて、ピストン付近の気体は温度が上がり、隣の気体は温度が下がる

である。

　ある程度引いた後、しばらく待って気体の状態が一様になったな、と思ったら今度は押して戻してみよう。今度はピストン付近の気体が圧縮されて温度が上がり、さっきとは逆に現象が伝わっていく。

↑この絵は単なる画像です。動きません。

　逆にピストンを押す時も同様で、↑の図のように、ピストンに近い部分は温度が上がった温度勾配ができる。

　ここで「ピストンを引く」「ピストンを押す」といういっけん「逆」に見える現象をしているが、細かく見ると「逆」になっていないことに注意しよう。これがこの後熱力学で何度も登場する「非可逆性」の最初の顕れである。

　ピストンを引いてから押して元の体積にまで戻したとする（上のプログラムで自分でやってみるべし）。温度もしばらく待っていれば外気温と同じ、つまり元の温度に戻る。こうして外気温に戻ると、完全に「元の状態に戻った」ということになる。

　力学でエネルギー保存則を考えるときは「一周回って戻ってきたのだから、エネルギーも元の状態に戻っている。だから仕事は0」というふうに考える。しかし、この場合の仕事は明らかに0ではない。

　プログラムを動かしながら、ピストンを引く時と戻す時で気体の圧力（青矢印）がどうなっているかを見ると、引く時は比較的圧力が小さく、戻す時は圧力が高くなっていることがわかる。

　↑の図でボタンを押していろいろな変化を起こしてみよう。よく観察すれば、「ピストンを引く時」と「ピストンを押す時」で起こる現象が対称でないことがわかるはずだ。

　結果として、ピストンが引かれる時に気体のする仕事の量は、戻す時に気体にされる仕事の量より大きいことになる。つまり、外部から仕事をしてやらなくてはいけない（気体は一周の間に負の仕事をする、と言ってもよい）。

　仕事をP-Vグラフというグラフ上に表現すると、もっとそのことがわかりやすいかもしれない。すぐそれをやってみたい人は、までジャンプせよ。

　少し先走っておくと、この「等温操作で気体を元の状態に戻すと、気体はその間に必ず負の仕事をしている」というのは熱力学で初めて登場する新しい物理法則であるとなる。

　気体が一周の間に負の仕事をしてしまう理由は「ピストンが引かれた時に気体がついていけないから」と「ピストンが押された時にピストン付近の気体が押されてその部分が特に圧縮されるから」だから、変化を十分ゆっくりと起こしてあげればそんなことは起きない。そのような理想的な操作（現実には起こせない）を「準静的操作」と呼ぶことにする。

　 　 　 　

準静的操作（断熱操作）

　次の例として、周囲と熱のやりとりのない状況で（断熱的に）閉じ込められた気体を考えよう。

　←ピストンは右半分の部分でしか動きません。
　

　まずピストンを引いてみよう。この場合も、温度や圧力は全体が一斉に変化するのではなく、ピストンに近い部分でまず「気体が膨張する」「気体の温度が下がる」という変化が起こり、それが伝わる。

↑この絵は単なる画像です。動きません。

　引いたピストンを押して戻すと、今度はピストンに近い部分で温度と圧力の上昇が起こり、それが伝わる。

↑この絵は単なる画像です。動きません。

　ピストンを引いてしばらくしてから今度は押して、元の体積に戻した時、温度は少々上昇しているはずである。

体積は元の状態に戻しているのに、温度が戻らないのはなぜか？？

この時気体のする仕事がどうなっているかを手がかりに考えてみよう。

　等温操作と違って断熱操作ではまわりと熱の出入りを断っているので、気体のした仕事、された仕事はそのまま気体のエネルギーの増減となる。「ピストンを引いて元に戻す」という操作をすると（ピストンが押される時、気体のされる仕事）＞（ピストンが引かれる時、気体のする仕事）となるため、気体のエネルギーは上昇してしまう、ということ。

　この場合は準静的に操作した場合に限り、行きと帰りの仕事が一致し、元に戻る（こういうの状況を「この操作は可逆である」という言い方をする）。

　準静的でなくても、ピストン引いた後押していって、温度が同じになるところでピタッと止めれば、温度は同じになりませんか？
　その場合、体積が同じになってないから、やっぱり元にはもどってないね。

　断熱操作と等温操作を比べると、熱の形でエネルギーが補充されて温度が一定になっているため、される仕事の状況は違う。詳細な計算は後でやるので、とりあえず今は「断熱操作と等温操作とでは、違うタイプのエネルギーが定義できるみたいだ」と感じておこう実は等温操作において「最大仕事」によって増減する量として「ヘルムホルツの自由エネルギー」という新しいエネルギーを作る、というのがこの後の流れ。。

　

最大仕事と準静的操作（P-Vグラフ付き）

　最後に、同じピストンの運動を、P（圧力）-V（体積）のグラフを見ながら行ってみよう。

ただし、ここでグラフにしている圧力Pとは、「気体全体の圧力」ではない（今考えている操作の途中では気体の圧力・温度は一様ではない）。グラフの縦軸であるPは、「ピストンに掛かる圧力」であり、いわば「ピストンに接している部分の気体の圧力」である。ピストンに接していない部分の気体の圧力は、もちろんこれとは違う。準静的ならば全体の状態が一様だから気体全体の圧力とピストンに接している部分の圧力は同じになる（ただし、このプログラムでは準静的な操作は起こせない）。

　下の図の青い線は、気体全体が常に等温を保った場合のP-Vの線である。等温操作でも断熱操作でも、実際の変化はこのようには起きない。

　

上の「初期状態に戻す。」ボタンを押すとP-Vグラフの軌跡もクリアされるので、いろんな状況での変化の様子を描いてみよう。

　たとえば等温操作でピストンを引き、しばらく待ってから戻した時のグラフが、

である。仕事はこの水色の線の下の面積だから、行き→と帰り←を比べると帰りの方が仕事の絶対値は大きい（ただし、収縮しているから気体のする仕事は負である）。

　こうして、等温操作で元に戻ってくる操作をすると気体がマイナスの仕事をしそうだ、ということがわかる。

　このように現実的な気体では（といっても、ここで見せているシミュレーションはまだまだ実在気体に比べれば簡単化されたモデルにすぎないのだが）、状態方程式から予想されるような変化は起きない。状態が「平衡状態」でない変化をするからである。

　「平衡状態」とは単純に言えば「気体の置かれる状況を変えずに放っておくと最終的に到達する状態」である。平衡状態では、シリンダー内の気体の温度・圧力が全く一様になっている。↑のプログラムで起こっている操作途中の状態は、ほぼすべて平衡状態ではない。

　変化が十分ゆっくりなら、「平衡状態」を保ったままで状態変化を行うことができると考えよう。そのような変化を「準静的操作」と呼ぶことにする。

　変化がゆっくりの場合の気体のP-Vグラフはより、「等温の線」（青色）に近づくことになる。実際にプログラムでピストンの移動速度を遅くしてからやってみよう。

　等温操作でピストンを引く場合に気体のする仕事を見ると、なるべく温度が下がらないように、ゆっくりと引くとよい（それが準静的操作）。そして十分にゆっくりと引いたときに、仕事は$NRT\int {\mathrm dV\over V}$と計算した仕事に一致する。この仕事を「最大仕事」と呼ぶことにしよう。現実的に（準静的でなく）ピストンを引くときは、最大仕事よりも小さい仕事になってしまう。つまり準静的にゆっくりと引く時が気体から得られるエネルギーが最大である。

　前にも述べたように、押す時に気体にされる仕事は、今度は$NRT\int {\mathrm dV\over V}$で計算される仕事より、絶対値が大きくなる。よって等温操作で元に戻る操作をすると、どうやっても気体は負の仕事をする。もし気体に正の仕事をさせることができるなら、気体が元の状態に戻っているのにエネルギーを仕事の形で取り出せたことになり、エネルギー問題なんて解決である（そうはいかないから困っている）。

　こうして「状態変化を一周させると気体が負の仕事をする」というがは、エネルギー保存則とは別の、もう一つの新しい物理法則として熱力学に登場してくることになるのである（熱力学第２法則ということになるのだが、それは今後のお楽しみ）。


　ここでは、「最大仕事」というキーワードと、最大仕事が実現する理想的な操作として「準静的操作」というものがどういうものなのか、なぜ大事なのかをまず理解して欲しい。それぞれを使ってどのように「等温操作におけるエネルギーにあたるものを定義するのか」ということを次に説明していきたい。