「数式が美しくないな」と思った人は、数式の上で右クリックして「Math settings→Math renderer」を「SVG」に設定してください。
と言われると、経験のある人の多くが
と反応するようだ。私も何度かやったことあるが、まじめに計算しようとすると確かにめんどくさい。
あるいは、ナブラと呼ばれるベクトルを $$ \vec\nabla=\vec{\mathbf e}_x{\partial\over\partial x}+\vec{\mathbf e}_y{\partial\over\partial y}+\vec{\mathbf e}_z{\partial\over\partial z} $$ と定義して($\vec{\mathbf e}_x,\vec{\mathbf e}_y,\vec{\mathbf e}_z$はそれぞれ$x,y,z$方向の単位ベクトル)、$\vec\nabla\cdot\vec\nabla$のように自乗(スカラー積)したものと定義しても良い。
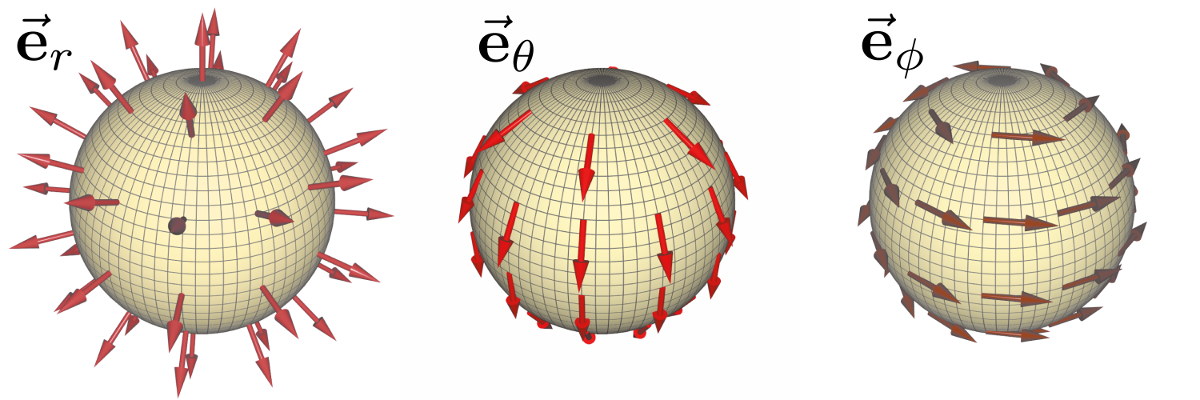
極座標でのナブラは、 $$ \vec\nabla=\vec{\mathbf e}_r{\partial\over\partial r}+\vec{\mathbf e}_\theta{1\over r}{\partial\over\partial \theta}+\vec{\mathbf e}_\phi{1\over r\sin\theta}{\partial\over\partial \phi} $$ と書かれている。なぜ $$ \vec\nabla=\vec{\mathbf e}_r{\partial\over\partial r}+\vec{\mathbf e}_\theta{\partial\over\partial \theta}+\vec{\mathbf e}_\phi{\partial\over\partial \phi} $$ じゃないのかというと、ナブラにおける微分は任意のベクトルを$\vec a$として、 $$ \vec a\cdot\vec\nabla f(\vec x)=\lim_{h\to0}{f(\vec x+h\vec a)-f(\vec x)\over h} $$ と定義されているからである。$\vec a$として単位ベクトルを取るとすると、この式の右辺は$\vec a$方向に$h$だけ離れた2点での差を取るという計算である。一方、θ方向にh進むためには、θを${h\over r}$だけ変化させなくてはいけない。φ方向ならば、φを${h\over r\sin\theta}$変化させなくてはいけないのである。よって、単なる${\partial \over\partial \theta}$ではだめで、 $$ \vec {\mathbf e}_\theta\cdot\vec\nabla f(\vec x)={1\over r}{\partial\over\partial \theta}f(\vec x),~~~\vec {\mathbf e}_\phi\cdot\vec\nabla f(\vec x)={1\over r\sin\theta}{\partial\over\partial \phi}f(\vec x) $$ であるべきなのである。$r\Delta \theta,r\sin\theta\Delta\phi$が「距離」という意味合いを持っていることを考えば、こうなることは納得できる。
これを自乗すると、ベクトルの内積を取って、 $$ \vec\nabla\cdot\vec\nabla={\partial^2\over\partial r^2}+{1\over r^2}{\partial^2\over\partial \theta^2}+{1\over r^2\sin^2\theta}{\partial^2\over\partial \phi^2} $$ となると思いたいところだが、そうならない。実際には、 $$ \vec\nabla\cdot\vec\nabla={1\over r^2}{\partial\over\partial r}\left(r^2{\partial \over\partial r}\right)+{1\over r^2\sin\theta}{\partial\over\partial \theta}\left(\sin\theta{\partial\over\partial\theta}\right)+{1\over r^2\sin^2\theta}{\partial^2\over\partial \phi^2} $$ または $$ \vec\nabla\cdot\vec\nabla={\partial^2\over\partial r^2}+{2\over r}{\partial\over\partial r}+{1\over r^2}{\partial^2\over\partial \theta^2}+{1\over r^2}\cot\theta{\partial\over\partial\theta}+{1\over r^2\sin^2\theta}{\partial^2\over\partial \phi^2} $$ となるのである。
いったい、この余計な部分はどこから出てくるのだろう。学生の頃から不思議でしょうがなかった。
そこでこの項目では、ラプラシアンの計算法の少し楽な方法を示すと同時に、「余計な部分はどこから来たのか?」を考えることにしよう。
ほんとは「こうやれば簡単に出る!」という方法を伝授したいところなのであるが、「簡単」と言いきれるほどには簡単に出ない。しかし、少なくても、「なぜ単純に自乗してはいかんのか」ということを実感することはできる。
一つの考え方として、「物理で使う計算方法で座標変換に強いものといえば?」と考えてみよう。答は「変分法」である。そこで、変分法を使って、ポアッソン方程式 $$ \triangle f=\rho $$ が出るような「作用」を考えてみる。直交座標ならこれは簡単に作れて、 $$ \int \mathrm dx\mathrm dy\mathrm dz\left( {1\over2}\left({\partial f(\vec x)\over\partial x}\right)^2 +{1\over2}\left({\partial f(\vec x)\over\partial y}\right)^2 +{1\over2}\left({\partial f(\vec x)\over\partial z}\right)^2 + \rho(\vec x) f(\vec x)\right) $$ である。$\vec\nabla$を使って書くならば、 $$ \int \mathrm dx\mathrm dy\mathrm dz\left({1\over2}\vec\nabla f(\vec x)\cdot\vec\nabla f(\vec x) + \rho(\vec x) f(\vec x)\right) $$ である。
または、 $$ \int \mathrm dx\mathrm dy\mathrm dz\left({1\over2}\sum_i \left({\partial_i f(\vec x)}\right)^2 + \rho(\vec x) f(\vec x)\right) $$ と書いてもいいだろう。
ここで、$\partial_1={\partial\over\partial x},\partial_2={\partial\over\partial y},\partial_3={\partial\over\partial z}$である。$\sum_i$はもちろん、$i=1,2,3$の和を取る。
この作用からオイラー・ラグランジュ方程式をつくると$\triangle f=\rho$になる。この計算を少しまじめに書いておく。オイラーラグランジュ方程式を作るには、作用の$f$に$f+\delta f$を代入したものを作り、それから元の作用を引く。そうしておいて出た答えの$\delta f$の一次までを取り、それが0になると置く。これを実行すると、 $$ \begin{array}{rl} &\int \mathrm dx\mathrm dy\mathrm dz\left({1\over2}\sum_i \left({\partial_i (f(\vec x)+\delta f(\vec x)}\right)^2 + \rho(\vec x) (f(\vec x)+\delta f(\vec x))\right) -\int \mathrm dx\mathrm dy\mathrm dz\left({1\over2}\sum_i \left({\partial_i f(\vec x)}\right)^2 + \rho(\vec x) f(\vec x)\right)\\ =&\int \mathrm dx\mathrm dy\mathrm dz\left(\sum_i \left({\partial_i f(\vec x)\partial_i\delta f(\vec x)}+{1\over 2} +\left({\partial_i (\delta f(\vec x))}\right)^2\right)+ \rho(\vec x) \delta f(\vec x)\right) \end{array} $$ ここで$\delta f$の2次の項は無視して、 $$ =\int \mathrm dx\mathrm dy\mathrm dz\left(\sum_i \left({\partial_i f(\vec x)\partial_i\delta f(\vec x)}\right)+ \rho(\vec x) \delta f(\vec x)\right) $$ 次に部分積分して、 $$ =\int \mathrm dx\mathrm dy\mathrm dz\left(-\sum_i \left({\partial_i \partial_if(\vec x)\delta f(\vec x)}\right)+ \rho(\vec x) \delta f(\vec x)\right) $$ となる。これが任意の$\delta f$に対して0となるためには、$-\partial_i \partial_if(\vec x)+\rho(\vec x)=0$でなくてはならない。
では、この計算を極座標でやるとどうなるだろうか??
記号$\partial_i$を、$\partial_1={\partial \over\partial r},\partial_2={1\over r}{\partial\over\partial\theta},\partial_3={1\over r\sin\theta}{\partial\over\partial\phi}$とおくことにする(この記号は一般的に使われているものではないので注意。この項目の説明に関してはこういう記号を使った方が楽なのである)。すると、作用を直交座標の場合と同じように $$ \int \mathrm dr\mathrm d\theta\mathrm d\phi r^2\sin\theta \left({1\over2}\vec\nabla f(\vec x)\cdot\vec\nabla f(\vec x) + \rho(\vec x) f(\vec x)\right)= \int \mathrm dr\mathrm d\theta\mathrm d\phi r^2\sin\theta \left({1\over2}\sum_i\left(\partial_i f(\vec x)\right)^2 + \rho(\vec x)f(\vec x)\right) $$ と書くことができる。
この式からオイラー・ラグランジュ方程式をつくると、直交座標と同様の計算になるように思うかもしれない。しかし、最後の部分積分で直交座標と極座標の差が出るのである。なぜなら、極座標の場合、積分要素は$\mathrm dx\mathrm dy\mathrm dz$ではなく、$\mathrm dr\mathrm d\theta\mathrm d\phi r^2\sin\theta$である。ゆえに、作用の変分は $$ \begin{align} &\int \mathrm dr\mathrm d\theta\mathrm d\phi r^2\sin\theta \left(\sum_i \partial_i f(\vec x)\partial \delta f(\vec x)+ \rho(\vec x)\delta f(\vec x)\right)\\ =&\int \mathrm dr\mathrm d\theta\mathrm d\phi\left(-\sum_i\partial_i\left( r^2\sin\theta \partial_i f(\vec x)\right)\delta f(\vec x)+ r^2\sin\theta\rho(\vec x)\delta f(\vec x)\right)\\ =&\int \mathrm dr\mathrm d\theta\mathrm d\phi r^2\sin\theta\left[-\sum_i{1\over r^2\sin\theta}\partial_i\left( r^2\sin\theta \partial_i f(\vec x)\right)+ \rho(\vec x)\right]\delta f(\vec x) \end{align} $$ となる。
括弧内を$\delta f$で割って、 $$ -{1\over r^2\sin\theta}\sum_i\partial_i\left(r^2\sin\theta\partial_i f(\vec x)\right)+\rho(\vec x)=0 $$ が極座標でのポアッソン方程式だということになる。この式の第一項は$−\triangle f(\vec x)$である。 $\triangle$とはつまり、
結局おつりの出る理由は、 直交座標の体積積分は$\mathrm dx\mathrm dy\mathrm dz$だが、極座標では$\mathrm dr\mathrm d\theta \mathrm d\phi r^2\sin\theta$であって、部分積分の時に$rr^2\sin\theta$がひっかかる。 ということで納得できる。
他の座標系でもこの方法は使える。
たとえば、三次元円筒座標を使うならラプラシアンは$\mathrm dx\mathrm dy\mathrm dz=\mathrm dr\mathrm d\theta \mathrm dz r$であり、$\partial_1={\partial\over\partial r},\partial_2={1\over r}{\partial\over\partial\theta},\partial_3={\partial\over\partial z}$である。この場合も、上と同様の計算ができて、
$$
\triangle={1\over r}{\partial \over\partial r}\left(r{\partial \over\partial r}\right)+{1\over r^2}{\partial^2\over\partial \theta^2}+{\partial^2\over\partial z^2}
$$
となる。
このようにして一見変なおつりが出てくる理由をちゃんと理解してしまえば、どんな曲線座標が出てきてもラプラシアンがどうなるかはすぐにわかるはずである。
では次にもう少しストレートな方法で「なぜ単純に自乗しちゃいかんのか?」を考えよう。とりあえず、$\vec\nabla$の自乗というのをまじめに書いてみると、直交座標では $$ \vec\nabla\cdot\vec\nabla= \left( \vec{\mathbf e}_x{\partial\over\partial x}+\vec{\mathbf e}_y{\partial\over\partial y}+\vec{\mathbf e}_z{\partial\over\partial z}\right)\cdot \left( \vec{\mathbf e}_x{\partial\over\partial x}+\vec{\mathbf e}_y{\partial\over\partial y}+\vec{\mathbf e}_z{\partial\over\partial z}\right) $$ 極座標では $$ \vec\nabla\cdot\vec\nabla= \left( \vec{\mathbf e}_r{\partial\over\partial r}+\vec{\mathbf e}_\theta{1\over r}{\partial\over\partial \theta}+\vec{\mathbf e}_\phi{1\over r\sin\theta}{\partial\over\partial \phi} \right)\cdot \left( \vec{\mathbf e}_r{\partial\over\partial r}+\vec{\mathbf e}_\theta{1\over r}{\partial\over\partial \theta}+\vec{\mathbf e}_\phi{1\over r\sin\theta}{\partial\over\partial \phi} \right) $$ となる。この式をみて早とちりのあわてものが「$\vec{\mathbf e}_r,\vec{\mathbf e}_\theta,\vec{\mathbf e}_\phi$は互いに直交して長さが1だから、$\vec{\mathbf e}_r\cdot\vec{\mathbf e}_r$のような同じもの同士の内積を残して計算すればいい」とやってしまうと、 $$ \vec\nabla\cdot\vec\nabla={\partial^2\over\partial r^2}+{1\over r^2}{\partial^2\over\partial \theta^2}+{1\over r^2\sin^2\theta}{\partial^2\over\partial \phi^2} $$ となるが、実際には $$ \vec\nabla\cdot\vec\nabla={\partial^2\over\partial r^2}+\underbrace{{2\over r}{\partial\over\partial r}}_{おつり}+{1\over r^2}{\partial^2\over\partial \theta^2}+\underbrace{{1\over r^2}\cot\theta{\partial\over\partial\theta}}_{おつり}+{1\over r^2\sin^2\theta}{\partial^2\over\partial \phi^2} $$ と、この早とちり計算法では出てこないおつりが出てきたものが正解である。
この早とちり計算法は何がまずいのだろう???
ここで「左にある微分は、右の括弧内を微分しないのか?」ということに気がつけば正解に一歩近づく。たとえば最初にある${\partial\over\partial r}$が、後ろにある${1\over r}$を微分したら??
この部分からおつりが出てくるのでは?と一瞬期待するが、ここからは出ない。確かに${\partial \over\partial r}\left({1\over r}\right)=-{1\over r^2}$となるが、この項は$\vec{\mathbf e}_\theta$に比例している。一方${\partial \over\partial r}$は$\vec{\mathbf e}_r$についているから、内積を取ると0になって効かない。${\partial \over\partial\theta},{\partial\over\partial\phi}$も同様である。
ここで「じゃあやっぱりおつりは出ないじゃないか」と落胆してはいけない。θ,φに依存するものは他にもあるのである。あからさまに書いていないものだからつい見落としがちなのだが、実は$\vec{\mathbf e}_r,\vec{\mathbf e}_\theta,\vec{\mathbf e}_\phi$は場所によって違う方向を向いているので、その微分は0ではない場合があるのである。
では以下で一つずつおつりの出方を確かめよう。まず第1項の$\vec{\mathbf e}_r{\partial\over\partial r}$の部分。この部分はおつりを出さない。なぜなら、$\vec{\mathbf e}_r,\vec{\mathbf e}_\theta,\vec{\mathbf e}_\phi$の全てが、$r$方向に移動しても向きが変わらないからである。
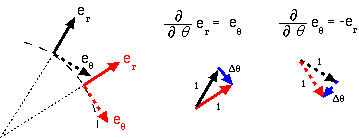
第2項の$\vec{\mathbf e}_\theta{1\over r}{\partial\over\partial\theta}$については、$\vec{\mathbf e}_r$の$\theta$微分は0ではないことが以下のようにわかる。図にあるように、$\theta$が$\Delta \theta$変化すると、新しい$\vec{\mathbf e}_{r新}$(図では、赤で書いているのが新らしい方)は元のベクトルで書くと、 $$ \vec{\mathbf e}_{r新}=\cos\Delta\theta\vec{\mathbf e}_{r旧}+\sin\Delta\theta\vec{\mathbf e}_{\theta 旧} $$ となる。これから、$\vec{\mathbf e}_{r新}-\vec{\mathbf e}_{r旧}$を計算して$\Delta\theta$で割ってから$\Delta \theta\to0$の極限をとれば、 $$ {\partial \over\partial\theta}\vec{\mathbf e}_{r}=\vec{\mathbf e}_\theta $$ である。$\lim_{\Delta\theta\to0}\cos\theta=1$に注意。
つまりは、 $$ \vec{\mathbf e}_\theta{1\over r}{\partial\over\partial\theta}\cdot\vec{\mathbf e}_r{\partial\over\partial r} $$ から $$ \vec{\mathbf e}_\theta{1\over r}\cdot\vec{\mathbf e}_\theta{\partial\over\partial r} $$ となって、さらに$\vec{\mathbf e}_\theta$の内積を計算して、 $$ {1\over r}{\partial\over\partial r} $$ というおつりが出ることになる。
$\vec{\mathbf e}_\theta$をθで微分すると答えは$-\vec{\mathbf e}_r$になる。よって、 $$ \vec{\mathbf e}_\theta{1\over r}{\partial\over\partial\theta}\cdot\vec{\mathbf e}_\theta{1\over r}{\partial\over\partial\theta} $$ は、 $$ -\vec{\mathbf e}_\theta{1\over r}\cdot\vec{\mathbf e}_r{1\over r} $$ である。しかし、$\vec{\mathbf e}_\theta$と内積をとると0になり、ここは効かない。$\vec{\mathbf e}_\phi$はθで微分しても変化しないから答えは0である。
次に、左の括弧内の微分 $$ \vec{\mathbf e}_\phi{1\over r\sin\theta}{\partial\over\partial\phi} $$ が後ろにかかるとどうなるかを考えてみる。同じように図を描いて考えるなりしてみれば、 $$ \vec{\mathbf e}_\phi{1\over r\sin\theta}{\partial\over\partial\phi}\cdot\vec{\mathbf e}_r{\partial\over\partial r} $$ のところからは、 $$ {\partial\over\partial\phi}\vec{\mathbf e}_r=\sin\theta\vec{\mathbf e}_\phi $$ による結果として $$ {1\over r}{\partial\over\partial r} $$ というおつりが出ることになる。
また、 $$ \vec{\mathbf e}_\phi{1\over r\sin\theta}{\partial\over\partial\phi}\cdot\vec{\mathbf e}_\theta{1\over r}{\partial\over\partial \theta} $$ からは、 $$ {\partial\over\partial\phi}\vec{\mathbf e}_\theta=\cos\theta\vec{\mathbf e}_\phi $$ のおかげで、 $$ \vec{\mathbf e}_\phi{\cos\theta\over r\sin\theta}\cdot\vec{\mathbf e}_\phi{1\over r}{\partial\over\partial \theta} $$ となって、 $$ {\cos\theta\over r^2\sin\theta}{\partial\over\partial \theta} $$ というおつりが出る。以上、3つのおつりをあわせると、正しいラプラシアンのできあがり。
こちらの方法で、なぜおつりが出るのかという理由は
ちなみに、一般相対論になじみのある人ならば、 $$ \triangle=g^{\mu\nu}\nabla_\mu\nabla_\nu=g^{\mu\nu}\partial_\mu\partial_\nu +g^{\mu\nu}\Gamma^\rho_{\mu\nu}\partial_\rho $$ と共変微分を使って定義やればおっけい。ちなみにここでの$\nabla_\mu$はいわゆる共変微分で、$\Gamma^\rho_{\mu\nu}$はクリストッフェル記号。もっとも、一般相対論になじみのある人は少ないし、なじみがあったとしてもクリストッフェル記号をささっと計算できる人は少ないだろう。しかし、 $$ g^{\mu\nu}\Gamma^\rho_{\mu\nu}={1\over\sqrt{-g}}\partial_\alpha\left(\sqrt{-g}g^{\alpha\rho}\right) $$ ということを知っていると、 $$ \triangle={1\over\sqrt{-g}}\partial_\mu\left(\sqrt{-g}g^{\mu\nu}\partial_\nu\right) $$ と書き直せることがわかって幸せである。実は一般の座標系でこの式を計算すればラプラシアンが出せる。このようなラプラシアンを出す作用は、 $$ \int \mathrm dV\sqrt{-g}g^{\mu\nu}\partial_\mu f\partial_\nu f $$ である。