「ニュートリノ振動」
ってなあに？
琉球大学理学部 前野 昌弘
右下に出ている矢印（＞、＜、▼、▲）の方向にカーソルまたはマウスクリックで移動できます。
基本「右へ右へ」で読めますが、ときどき「下に」補足説明を読みに行ってください。
Escで目次になります。
途中の質問、ツッコミは大歓迎
質問することは、恥ではありません。
- 「こんなこともわからないの？」と思われると恥ずかしい
- 大丈夫、あなたがわからないってことは、きっと他にも
わからない人はいるから。それに本当に恥ずかしいのは「わからないのにわかったふりをすること」ですよ。
質問することは、話者への非難ではありません。
- 「ここがわからない」と言ったら、説明してくれている人に失礼？？
- そんなこと考えてはいけません。話す人にとっては「あなたにわかってもらうこと」が一番大事なんです。話す人にとっても聞く人にとっても残念な結果は「わからないままで話が終わっちゃうこと」ですよ。
質問することは、互いの理解を深めるために必要です。
科学の世界では
「いい質問する人＞ばかな質問する人＞＞＞＞＞＞＞＞＞＞＞＞＞＞＞＞＞質問しない人」です。
「ニュートリノ振動」
って何なのよ！
そもそもニュートリノって何？
ニュートリノが振動するって何？
振動と質量に何の関係が？？
どうやってそんなことがわかるの？
それがあったら何か役に立つの？
と謎は尽きぬのですが...
まずニュートリノの歴史
- ニュートリノの存在が最初に示唆されたのは1899年のラザフォードの実験。彼は「β崩壊」と呼ばれる現象を観測していた。
- 1913年、このβ崩壊を詳しく調べたチャドウィックは、出てくる電子のエネルギーが計算に合わないことに気づく。
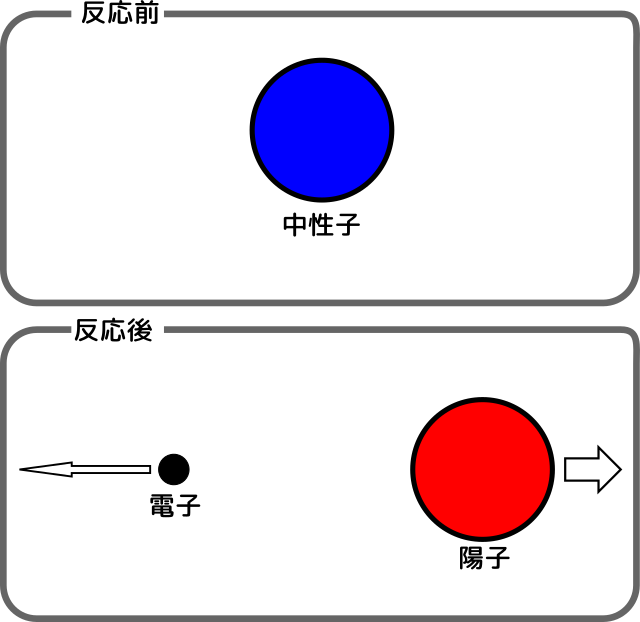
反応後にもう一つ「見えない粒子」がいると仮定すれば。
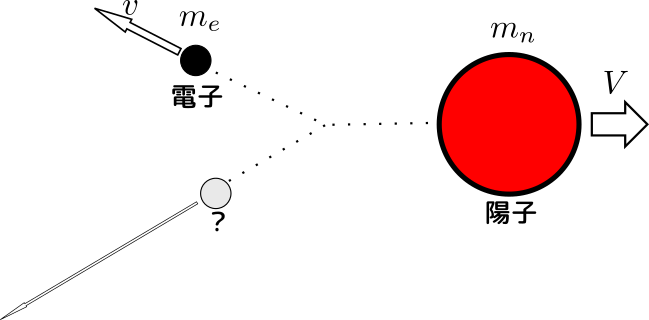
謎の粒子がβ崩壊のエネルギーの一部を持って行ってしまうと考えると、計算が合う！
逆に言えば、この謎の粒子がないとエネルギーすら保存しないのだ！
この謎？の粒子を「ニュートリノ」と名付けよう。
「ニュートリノ」は「中性の小さな粒子」という意味。
いかにも「その場しのぎ」に思えるアイデアだが、
結果は「当たり」だった。
で、その粒子であるニュートリノが振動するとは？
注意：この「振動」は物体がいったりきたりするという「振動」ではありません。
その後わかったことですが、ニュートリノには実は３種類あります。
- 電子ニュートリノ（νe）
- ミューニュートリノ（νμ）
- タウニュートリノ（ντ）
です。
この三つのニュートリノが（運動していくうちに）変化する、というのがニュートリノ振動です。
３種類の違いについては▼を見よ。
３つのニュートリノの違いは、その反応の「素過程」の違いです。
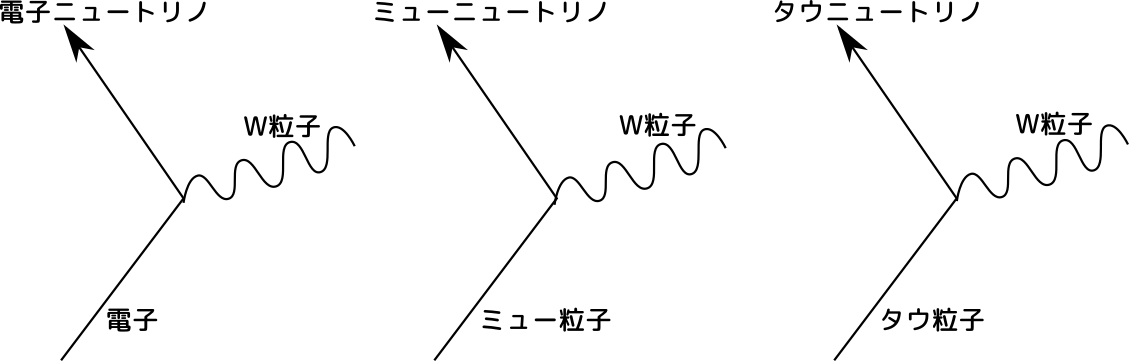
一番左の図は、「電子がW粒子と電子ニュートリノを出す」という相互作用の様子を表現した図です。
（図では上を未来にして書きました）
（他にも素過程はありますが、省略してます）
左上のような図があると、他にもこんな図で表される相互作用があります。
（他のは一つ目の「線の入れ替え」で得られます）
実は、話の最初であげた「β崩壊」は
という相互作用だったのでした。（つまり、正確には「謎の粒子」は反電子ニュートリノだった）
「場」って何？―電場の例
なぜニュートリノの種類が変わるか？―それを知るには「場」のことを知らなくてはいけません。
そこで「場」というものについて考えましょう。
もっともよく知られている「場」は「電場」と「磁場」です。（教科書によっては「電界」「磁界」になっていることもあるけど、方言のようなもので、同じ言葉です）
▼に、電場の図に関する説明があります。
正電荷と負電荷。
正電荷は電場の「湧き出し口」、負電荷は電場の「吸込口」になります。こうして正電荷と負電荷は引き合います。
正電荷と正電荷。
この場合、正電荷どうしが反発します。
重なった正電荷と負電荷。
正電荷と負電荷がほぼ重なると、まわりの電場は消え去ります。
原子は電気を持っているのに、普段気づかないのはプラスマイナスが消し合っているからです。
「場」と「粒子」
ここまで説明した「場」は電場と磁場でしたが、実はこの世にあるもののほとんど（たぶん、全部）は「場」でできています。
我々の身体は分子や原子でできていて、原子はさらに小さい電子や陽子や中性子でできていますが、これらの粒子（と思われているもの）の正体は実は「電子の場」「陽子の場」「中性子の場」なのです。
と言ってもなんのこっちゃ？でしょうから、
まずは「粒子が場ってどういうこと？」というイメージを、場についてのアニメ（ここをクリック）で見てみましょう。
▼「補足説明」が下にあります。
我々が「素粒子」と呼んでいるものは、この「場」にできた「盛り上がり部分」だと考えてください。
世の中み〜んな波ばかり♪
物質がこういう「波」の性質を持っているということは、20世紀の初め頃に、原子・分子、そして光の研究をしていた物理学者達が気づきました。
それが量子力学です。
図に描いたような「原子核という粒の周りを電子という粒が回っている」というイメージは、実は正しくありません。
原子核の周りにできる波についてのアニメ（ここをクリック）で見てみましょう。
▼「よくある質問」が下にあります。
Q:じゃ、原子の中の電子が回っているというのも波なんですか？
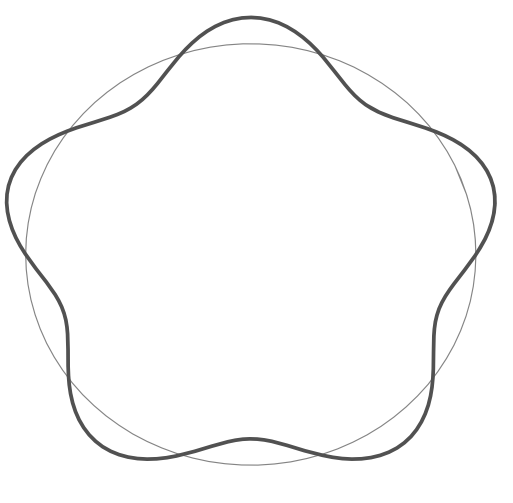A:そうです。あれも波です。ほんとは「回っている」んじゃなくて、周りに波ができてます。
Q:波だとすると広がると思うんですが、物質の波ってのはどうして広がらないんですか？
A:ここのプログラムで見せている波ってのは、互いに力を及ぼしたり、エネルギー与えたりしないような波なので、広がる一方です。
しかし、たとえば原子核と電子だと、電磁力を及ぼし合っています。電磁力は古典力学では「力」として働きますが、量子力学では「波を曲げる（屈折）」作用のように働きます。その屈折作用により、電子の波は原子核の周りを回ってすすみ、広がりません。
水素原子は、陽子の場と電子の場が相互作用して互いを屈折させることで存在できるのです。
波なら広がって消えてしまいませんか？
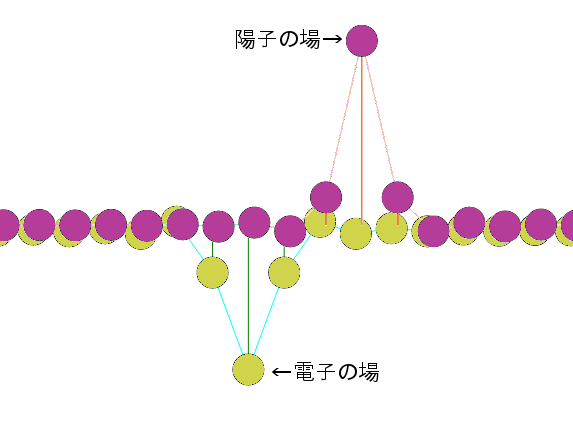
と、思うのも当然ですが、量子力学でいう「波動関数の収縮」という現象（あるいは「射影仮説」という原理）により、粒子が測定・観測されるときは（その観測装置の精度の範囲で）一点で見つかります。
このあたりの話は詳しく話しませんが、量子力学の波動関数の収縮（または射影仮説）により、「波」であるところの「場」が粒子性を持つという二重性が現れています。
この世は全て「場」でできている
信じられないことかもしれませんが…
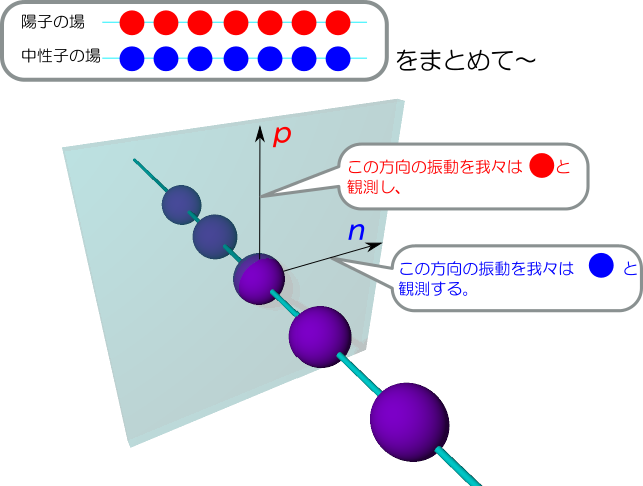
何もないように思える「真空」にも、それぞれの粒子に対応した「場」があります。
我々が「粒子」と呼んでいるのはその「場」が振動している状態（励起状態と言います）です。
粒子は言わば、
場にできた「さざ波」
なのです。
これらのさざ波は「架空の方向」に振動しますが、その架空の方向の違いが粒子の種類の違いです。
粒子が「場のさざ波」
ならば、「質量」とは？？
さっきまで見せていた波は止まれない波
だったということに気づいていますか？？
気づいてなかった人はもう一度アニメ（ここをクリック）を見よう。
ここまで見せた「場」の波は、実は質量のない粒子に対応するものだったです。
質量のある粒子と質量のない粒子
質量は「加速しにくさ」なので、質量が小さいと
「ほんの少しの力でビュ〜〜んと加速してしまう」
ということになります。
質量が0だというのは、究極の状態で、「何もしなくても可能な最大の速度で走る」のです。
相対性理論から粒子の速度は光速を超えられないことがわかっているので、質量が0の粒子は「常に光速で走っている粒子」ということになります。
光の粒子である光子、重力場の粒子である重力子などが質量が0の粒子の例です。
質量のある粒子に対応する場は
どのようになるか？
アニメ（ここをクリック）で見ましょう。違いは、バネです。
新しいアニメでは、●と●をつなぐバネ（水色）だけではなく、●を原点に戻そうとするバネ（緑色）が加わっています。
これがあることで、●の振動がすぐに隣に伝わらずに、「その場で振動」することができるようになります（つまり、粒子が止まることができる）。
この緑のバネが加わったことが、粒子に質量を与えます。
▼補足説明が下にあります。
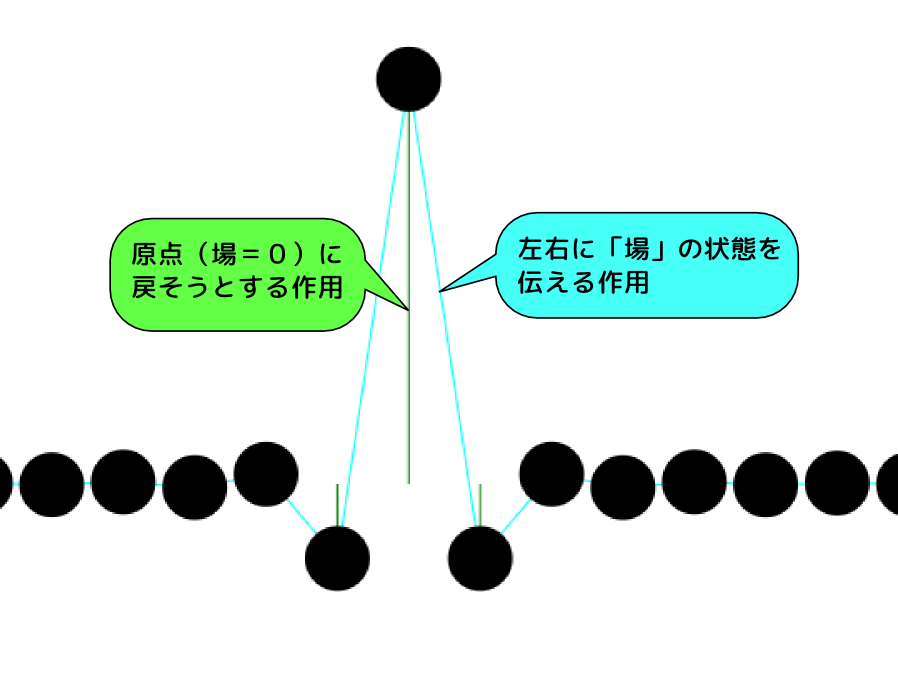
この緑のバネが強いとその場所での振動が長く続き、水色のバネが強いと振動が素早く伝わっていく。緑のバネが強ければ強いほど、重い。
ここまでのまとめ
日常生活で作られた常識からは信じがたいかもしれませんが、この世界にある物質は全て、このような、「場」つまり
空間の各点各点に存在し、「架空の方向」に振動することができる「架空のバネ」の集まり
でできています。
「ニュートリノ振動」という現象は、この「場」で作られた世界で起こる現象です。
というわけで、ここまでで
物質って「場」だったんだ！
という認識を持ってください。
物理の醍醐味は世界の認識を変えること。
ではニュートリノの話に
何もないと思われる「真空」にも素粒子の数だけの「場」があって、その場が振動すると我々は「あ、ここに粒子がいる」と感じます。
ニュートリノは３種類ありますが、３種類を考えるのはたいへんなので、まずは２種類で考えます。つまり、真空の各点各点に、２種類の「架空のバネ」がいて、それらが振動すると「ニュートリノがある」と我々は観測します（←この観測がとても難しい、ということは前に述べた通り）。
ああ、この「真空にある架空のバネの振動がニュートリノ振動ですね？というのは早とちり。
ニュートリノにかぎらず、真空にある架空のバネの振動は「素粒子」です！
二種類のニュートリノの振動のイメージ
とりあえず二つのニュートリノはその１（x方向のニュートリノ）とその2（y方向のニュートリノ）とする。空間のある一点で起っている振動を表現したのが左の図（これが空間の各点各点で起っている）。
この振動をアニメ（ここをクリック）で見てみよう。
この段階では、二つの振動は別々に独立で、いつまでも同じ振動がえんえんと続く。つまり「ニュートリノその1はいつまでもその1のまま、その2はいつまでもその2のまま」である。
▼にプログラムを動かしたところの説明あり。
が横方向の振動、
が縦方向の振動である。横方向の方がバネが強い（ポテンシャル勾配がきつい）ときは横方向の方が速く振動する。
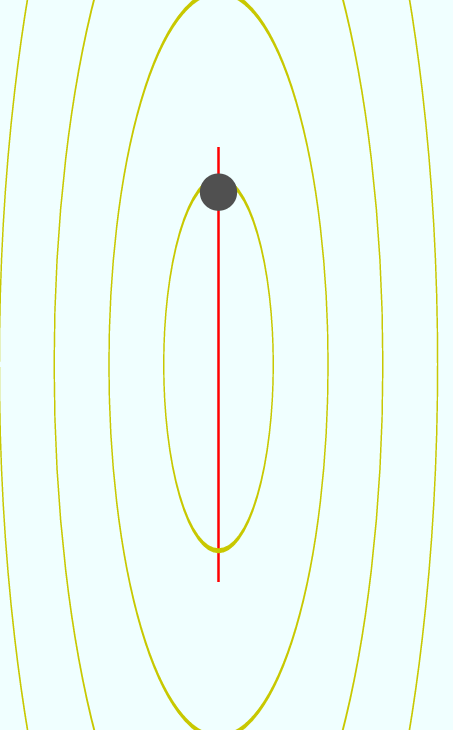左のように、バネの強さ（質量）を変化させると振動の様子も変わるので確認しよう。
二種類のニュートリノの振動のイメージその２
さて、次に振動を左図のように斜めの場所から始めるとどうなるか、を見てみよう。
つまり「その1（x方向）でもその2（y方向）でもない方向に振動が起こったら？」と考えるのである。
この振動もアニメ（ここをクリック）で見てみよう。
「ペンデュラム サンドアート」で検索すると、この動きをする玩具（たとえばこれ）が出てきます。
x方向とy方向のときは同じ振動が続いたが、斜め45度方向で振動させようとすると、一直線の振動は起きない。
▼にプログラムを動かしたところの説明あり。
(1,1)から始めると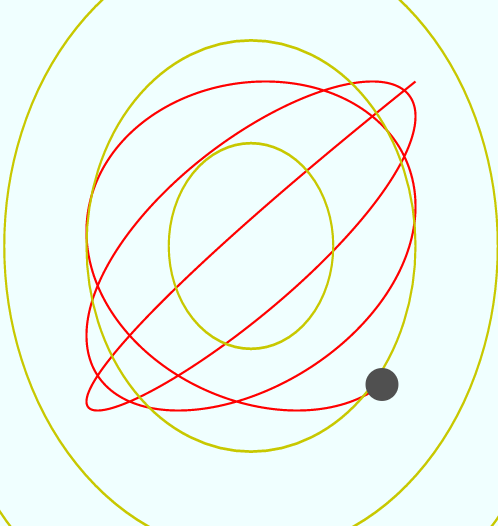
のように軌跡が描かれる。
しばらく待っていると
のように四角の中が埋め尽くされるように動く。
▼に続きあり。
しばらく待っていると、
になったり
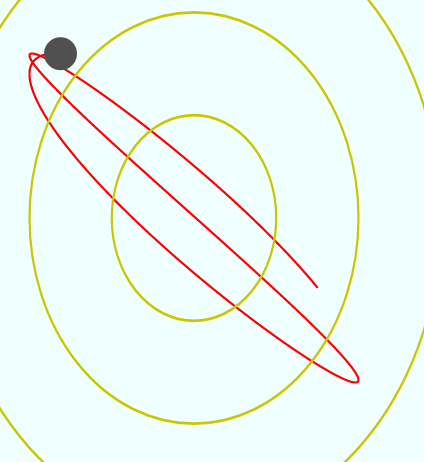になったりを繰り返す。この二つの状態がそれぞれミューニュートリノとタウニュートリノだと思えばよい。これが「ニュートリノ振動」なのだ。
しばらく動きをいろいろ眺めて「あ、ミューからタウに変わった」などと楽しもう。
▼数式での説明あり。
二つの方向の「運動方程式」は
d2Xdt2=−ω2X
と
d2Ydt2=−Ω2Y
のように書ける。
XとYは違う角振動数（ωとΩ）で振動するから、最初(1,1)の場所にいてX=Yであっても、その関係がずれていく。そのためあのような軌跡になる。
ちなみにこの角振動数比が整数になるようにすると、周期的運動になる。試してみよう。
ニュートリノ振動
前のページで見せたように、斜め方向に始まった振動は同じ方向では続かない。
たとえば「ミューニュートリノが生成する」とき、実は斜め45度の位置から振動が始まるとすると、振動するうちに「ミューニュートリノじゃないニュートリノ」が現れてくる。
このようなことが起こるのは、強さの違うバネ（質量の違う場）が混ざってしまったときである。
▼にプログラムを動かしたところの説明あり。
バネの強さを同じにしておくと、(1,1)から始めても
のように、一直線上を振動する。
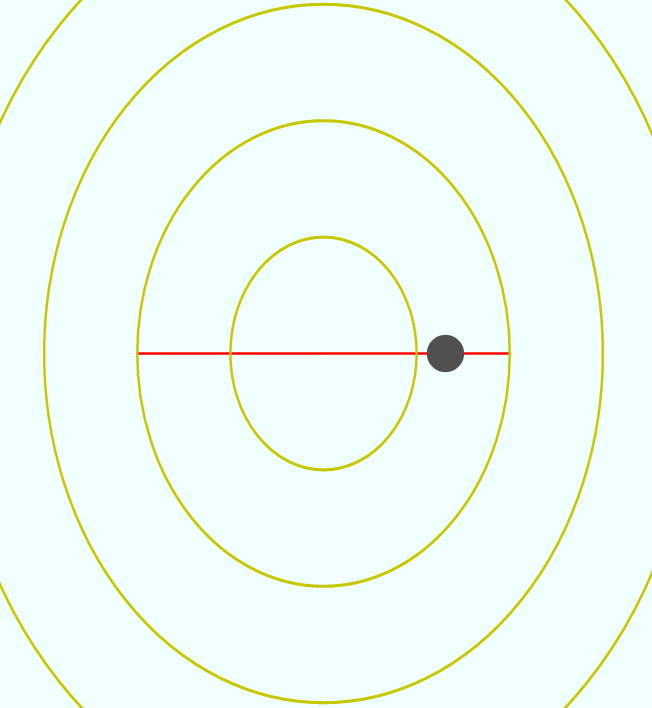
力学の問題としてみれば、力の方向は等ポテンシャル面に垂直だから、等ポテンシャル面がきれいな円になっていれば、力が常に中心方向を向く（楕円だとそうじゃない！）
ニュートリノ振動はなぜ起こる？
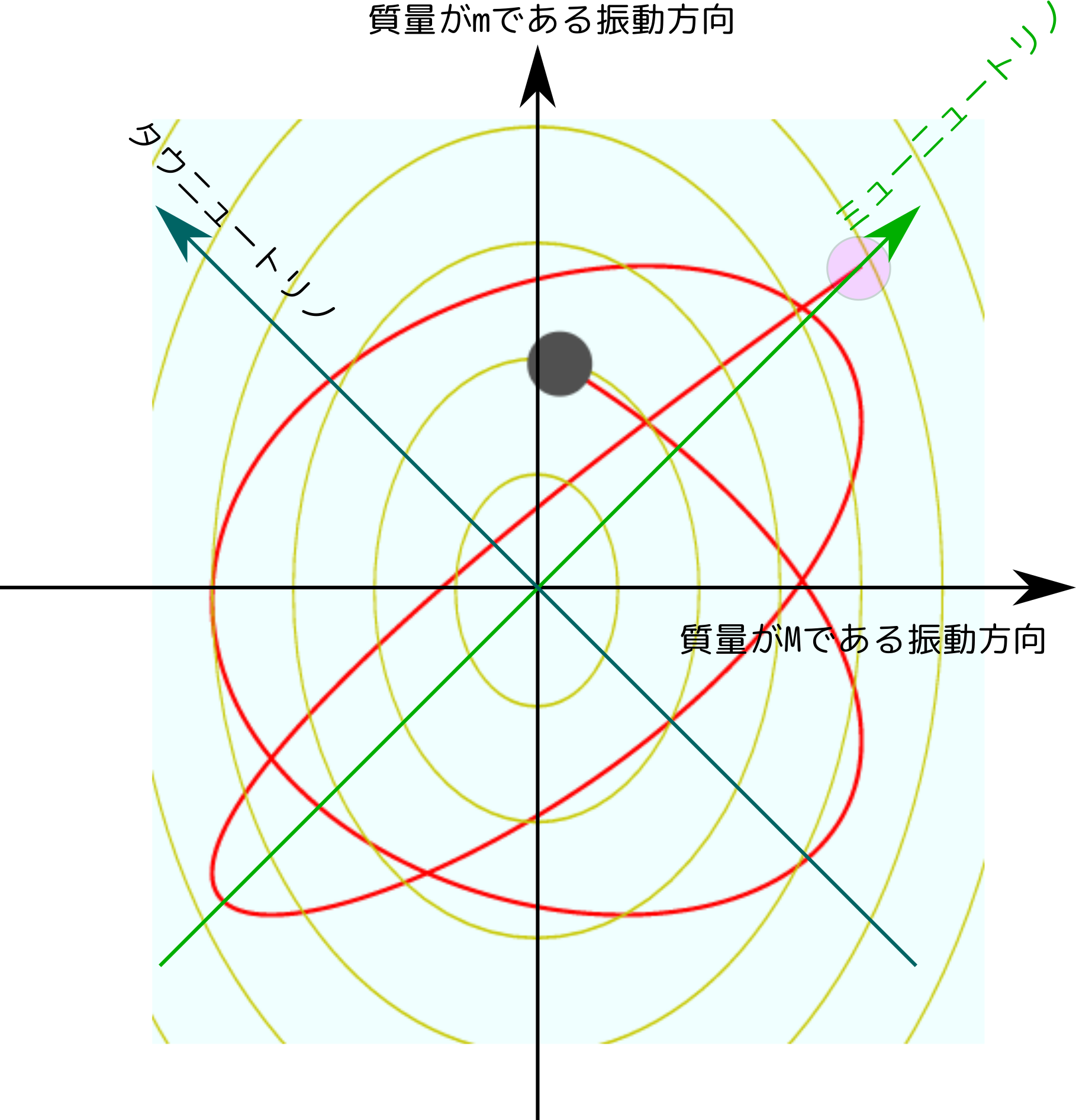
「場の振動」こそが我々が「素粒子」と観測するものである。架空の空間における「振動の方向」が「粒子の種類」に対応しているのだが、「質量（すなわちバネの強さ）」が一定になる「振動方向」とニュートリノの種類の「振動方向」が一致していない場合、振動していくうちに元々の粒子のものとは違う方向の振動が始まり、「粒子が混じる」ということが起こる。
逆に言えば、電子など我々のよく知っている物質ではこの混じりあいがないか、起こってもすごく小さい。だから粒子が変化しないのが当たり前のように思える。
だが、それは「偏見」だということをニュートリノ振動（ちなみに粒子の混合が起こるのはこれだけではない）は教えてくれる。
神岡で行われた実験
よって、
- できたてのミューニュートリノ
- できてから走ってきたミューニュートリノ
を比べると、後者ではミューニュートリノの割合が減る現象が起こる。
2015年のノーベル賞は、地球の大気で発生したミューニュートリノの観測結果を調べて、その現象を確かめた実験に対して送られた。
（スーパーカミオカンデ公式ホームページの大気ニュートリノ説明ページも参照のこと）
ニュートリノに質量がある証拠
アニメ（ここをクリック）で見たように、バネの強さすなわち質量が同じならば、どのような角度の振動が起こっても常に同じ一直線上で振動が続く。ニュートリノの種類が変わるという現象が起こるためには、質量（すなわちバネの強さ）が架空の方向ごとに違っていなくてはいけない。
昔はニュートリノは質量がないと思われていた（電子ニュートリノもミューニュートリノもタウニュートリノも）。しかしそれでは「みな同じ強さのバネ」だから振動現象は起きなくなってしまうのである。
まとめ：わかって欲しいこと
- この世界を作っているものが「場」であること。
- その「場」に起こるさざ波が物質を作っていること
- 場のさざ波である粒子はときには「混ざり合ったり、時間が経つと変化（振動）したりすること
結果として「物質の種類が途中で変わる」なんてことまでわかるのですが、これらが「場の理論」が我々に教えてくれることです。ニュートリノ振動の発見は、場の理論の正しさの確認を一つ付け加えました。
まとめその２：物理学が目指すこと
こうして人類は世界の仕組みを知ることに少しずつ近づいています。
「場の理論」といっても、それは振り子の運動のような「普通の物理」の延長上にあるものです。
しばしば基礎理論は何の役に立つ？と言われますが、これから先どのように科学が進むにしろ、我々の知っている「基礎理論」が正しいことを確認していくことは大きな意味があります。
人類が世界の仕組みを知らないままなのは「嫌」じゃないですか？―それに、仕組みを知った先には今は思いもつかない「役に立つこと」があるかもしれないし。
