の掛算をすればよい。では三角形の面積は？---以下では三角形の中では一番面積を考えることが容易である直角三角形の場合で考えよう。積分とは何か？と尋ねると微分の逆ですと答える人が多い。それは間違いではないが、実際のところは微分には微分の、積分には積分の、それぞれの意味があって、その意味が「逆」であることを示している。
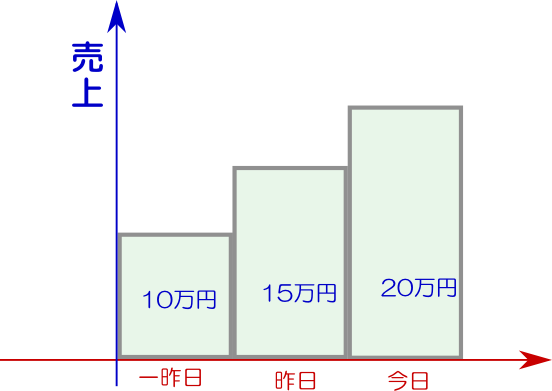
たとえば「一昨日の売上は10万円、昨日の売上は15万円、今日の売上は20万円だった」というなら、この３日間の売上合計は$10+15+20=45$万円である。これは普通の足し算である。平均の売上は？---と言われたら${45\over 3}=15$万円ということになる。これは普通の「足算」と「平均」である。
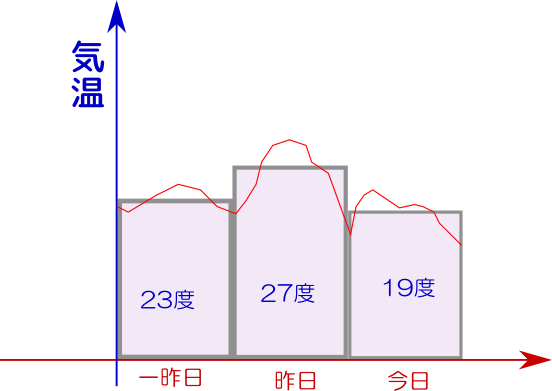
同様に「一昨日の気温は23度、昨日の気温は27度、今日の気温は19度だった。平均気温は？」と言われたら、${23+27+19\over 3}=23$度ということになる。しかしここで、「いや待て。一昨日の気温は23度というが、朝は18度ぐらいで、昼は25度を超えていたぞ」という文句をつける人がいるかもしれない（この「文句」はいちゃもんでもなんでもない、正当なものだ）。確かに売上のように「１日に何円」と明確に決まる量と違って、気温というのは連続的にどんどん変化するものである。この時「平均」を求めるための「足算」はどのように行えばよいのだろうか？？？
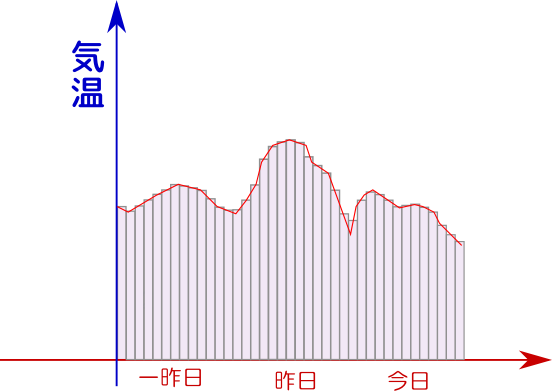
すぐに思いつく対策は「１日ごとに気温を考えるのではなく１時間ごと、あるいは30分ごと、それでもダメなら1分ごとなり1秒ごとなり、なるだけ短い時間感覚で気温の測定を行って平均しよう」ということだ。この連続的に変化する量を足すのに必要な計算が積分である。後で定義する積分がまさにそういう量になっている。
長方形の面積を計算しろ、と言われれば、小学校で習ったように
の掛算をすればよい。では三角形の面積は？---以下では三角形の中では一番面積を考えることが容易である直角三角形の場合で考えよう。
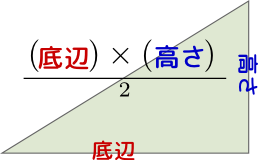という計算をすればよいと、これまた小学校で習う。直角三角形の面積は長方形の面積の半分であることは図形で説明することも、もちろんできる。
直角三角形の面積を以下のように考えることが「積分」の考え方である。
(この場所の高さ)は0から(高さ)まで変化するから、平均を取ると（どうやって取るのかはまた後で考えよう！）、${({高さ})\over 2}$になると考えると、三角形の面積の式が出てくることになる。
つまり、積分は掛算なのだが、「変化する量」との掛算なのである。
そんな「掛算の進化形」を作らなくとも、三角形の面積は見ればわかるだろう---と思う人もいるかもしれない。もちろんそうなのだが、これがもっと違う形であっても（たとえば円であったり、放物線の形だったりしても）面積がちゃんと計算できる方法を作りたい。
また、もっと積分のありがたみがわかる例として、立体の場合がある。直方体の体積が$(底面積)\times(高さ)$なのに対し、角錐の体積は${(底面積)\times(高さ)\over 3}$である。この${1\over 3}$はどこから来たのか（これを図形的に示すのは、少なくとも簡単にはできない）。これもやはり「変化する量との掛算」を行った結果なのである（実際にどう計算するかは後で示そう）。
ここで「足算の化け物」「掛算の進化形」としての積分を紹介したが、実はこの二つはどちらも「グラフの面積」で表現できることがわかった。そこで次の節では「グラフの面積を計算するにはどうするか？」を考えていこう。
もっとも簡単な「直角三角形」から始める「そんなの知っているよ！」と言いたくなる気持ちはわかるが、ここで開発した方法を使ってとても計算できそうにない図形の面積も計算できるようになる。これはあくまで「最初の練習」である。。
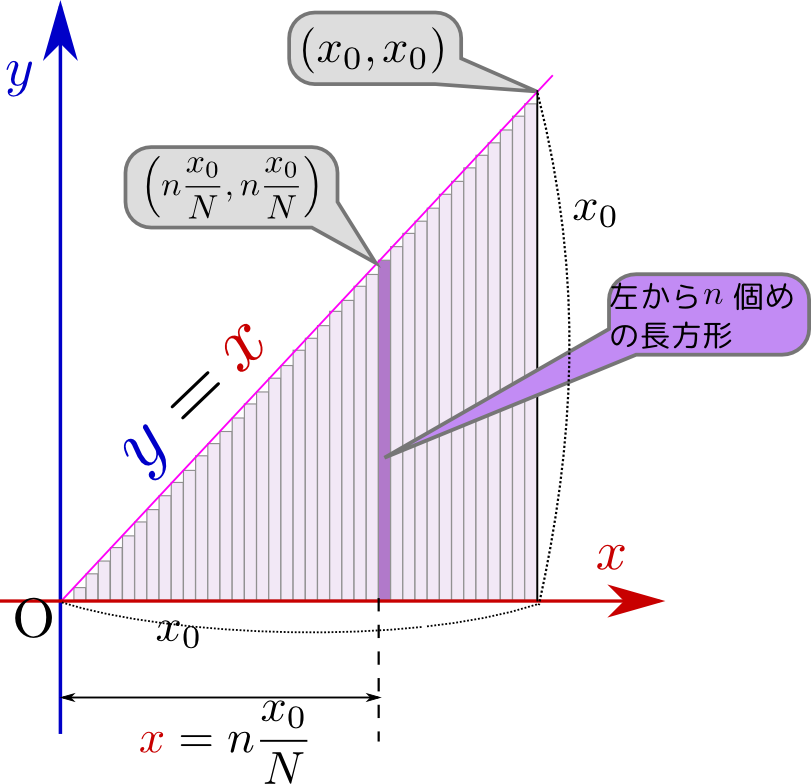
図のような直角三角形（その三つの角が$(0,0)(x_0,0),(x_0,x_0)$になるようにする）の面積を考える。まず底辺を$N$分割しておく（後で$N\to\infty$とする）。切り取られてた一個の長方形は、横幅${x_0\over N}$で縦が$n{x_0\over N}$であるから、面積は$n{(x_0)^2\over N^2}$である。これを$n=1$から$n=N-1$まで足す。
\begin{equation} \sum_{n=1}^{N-1}n{(x_0)^2\over N^2} ={(x_0)^2\over N^2} \sum_{n=1}^{N-1}n =(x_0)^2\times{N-1\over 2N}\label{NNN} \end{equation}上の式では、$\sum_{n=1}^{N-1}n={N(N-1)\over 2}$という和の公式を用いた。最後にある${N-1\over 2N}={1\over 2}-{1\over 2N}$という量は${1\over 2}$より${1\over 2N}$だけ小さい数だから、$N$をどんどん大きくしていけばこの部分が${1\over 2}$となり、長方形の集合の面積は${(x_0)^2\over 2}$、つまり${(底辺)\times(高さ)\over 2}$に下から近づいていく「より小さい」という大小関係を守りつつその値に近づいていく場合は「下から近づく」と表現する。逆の場合は「上から近づく」である。。ただし、これで証明できたのは、長方形の集合の面積$\leq{(底辺)\times(高さ)\over 2}$正確には、$\leq$ではなく$<$が証明されている。そして、$N\to\infty$においてこれが$=$になるだろう、というのは今の段階だはまだ単なる「予想」でしかない。である（まだ等式ではない）。
絵の右にあるのが浴槽で、上にある蛇口から水が注ぎ込まれている。右の方にあるレバー
をひねることで水が出ると思って欲しい（レバーは赤い印のところで水が止まり、時計回りに回すことで出る水の量が増えていく）。
グラフの横軸は時間であり、縦軸はvすなわち「1秒あたりに流し込んでいる水の量」である。（１秒あたりに流し込んでいる量）×（秒数）で「流れ込んできた水の量」が計算できるが、それはちょうどグラフの水色の長方形の面積になっている。
つまり、溜まっている水の量が、グラフの面積（水色に塗ったところ）で表現されているのがわかるかと思う。
最初の状態では、５段階に分けてレバーをひねり、少しずつ水の流量を増やしている。この段階数を∞にしていこう、というのが積分の考え方である。
このプログラムではNを（ある程度までだけど）大きくできるので、どんどん大きくしてみよう。Nが十分大きくなれば、この現象は「連続的に流水量を増やしていった場合」と変わらない、ということがわかるだろう。N→∞の極限を取ることを考えれば、最終的結果はグラフの下の部分（三角形）の面積となる、ということである。
積分は「単なる定数vとｔの掛け算ではなく、変化するvとtの掛け算である」という意味では「掛け算の進化系」である。
そして、ちょっとずつ変化する量×Δt（図の水色長方形）をえんえんと（無限回！）足した結果だと思えば「足し算の化け物」でもある。
そこで、長方形の作り方をちょっと変えてみる。具体的には上では「常に長方形が三角形の下にある」ようにしたが、「常に長方形が三角形より上に飛び出ている」ようにするのである（「上からの極限」）。
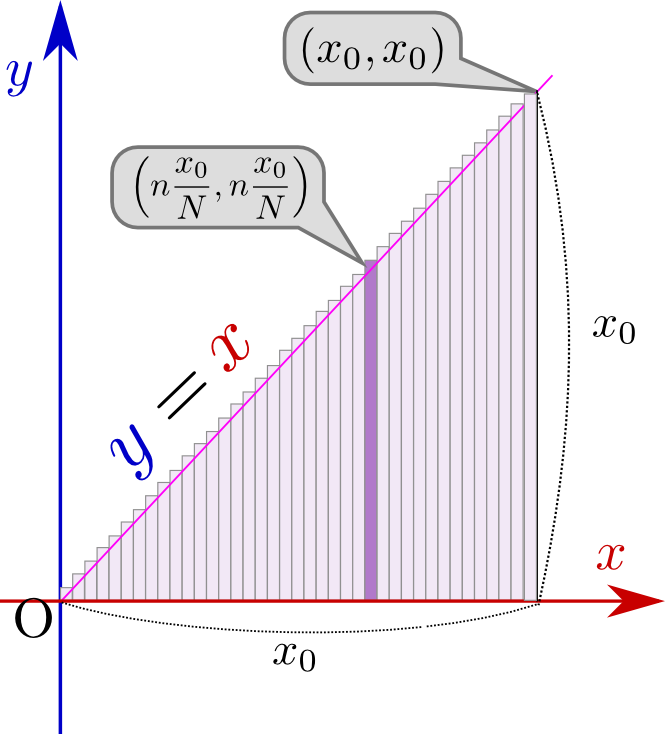
すると今度は足すべきものが$n=1$から$n=N$までとなり、
\begin{equation} \sum_{n=1}^{N}n{(x_0)^2\over N^2} ={(x_0)^2\over N^2}\underbrace{\sum_{n=1}^{N}n}_{{N(N+1)\over 2}} =(x_0)^2\times{N+1\over 2N} \end{equation}となる。今度は最後に${1\over 2}+{1\over 2N}$があり、これが$N\to\infty$で${1\over 2}$に上から近づく。よって、この極限の取り方では長方形の集合の面積$\geq{(底辺)\times(高さ)\over 2}$が証明できたことになる。
あわせて
\begin{equation} \left({下からの極限による\atop 長方形の集合の面積}\right)\leq{(底辺)\times(高さ)\over 2}\leq \left({上からの極限による\atop 長方形の集合の面積}\right) \end{equation}となり、極限を遂行すれば、三角形の面積$={(底辺)\times(高さ)\over 2}$が示せた。
以下で、これをもっと一般的な関数（「一般的なグラフ」と言ってもいいし、「一般的な図形」と言ってもいいだろう）に対して同様の計算を行っていく。そこで少し記号を整理しよう。上で考えた${x_0\over N}$という微小長方形の横幅は「${x}$の変化量で、後で0になる極限を取るもの」という意味を持っているから、微分の時と同様に、$\mathrm dx$と書くことにしよう同じ意味を持つ量なので、同じ記号を使っているのである。。${x}=n{x_0\over N}$であることも使うと、三角形の面積は（面積が小さくなるように考えた場合）
\begin{equation} \sum_{n=1}^N n{x_0\over N}\times {x_0\over N}=\sum_{n=1}^N{x}{\mathrm dx} \end{equation}と書くことができる。$N\to\infty$という極限は$\mathrm dx\to0$という極限であり、その極限において今考えている和は「無限個の区間の足算」に変わる。
$1$から$N$まで$n$を変化させつつ足すということが$N\to\infty$（$\mathrm dx\to0$）という極限を取ることによって、$0$から$x_0$まで${x}$を変化させつつ足すに変わったのだから、記号の方も$\sum_{n=1}^N$ではない別の記号$\int_0^{x_0}$を使う$\int$の読み方は「いんてぐらる」。記号自体は「積分記号」と呼ぶ。元々は「和」に対応するラテン語（summa、英語のsummation）のsを伸ばして作られた（ライプニッツによる）。ことにする。
こうして新しい記号で書いた$\int_0^{x_0} {x}\mathrm dx$が「定積分(definite integral)」という演算である（後で「不定積分」も出てくる）。この書き方では結果を
\begin{equation} \int_0^{x_0}{x}\mathrm dx={(x_0)^2\over 2}\label{sekibunx} \end{equation}と表すことができる。
$\int_a^b$と書いた時の$a$は「（定積分の）下限」、$b$は「（定積分の）上限」と呼び「どこからどこまでを足したのか」を示す。領域$a<{x}< b$は「積分区間」と呼ぶ。上の例では$0,x_0$が下限と上限だったが、もちろんどこからどこまでを足すかは状況によって変わる。
定積分はもちろん、いろんな関数について実行できる。$f({x})$という関数を「$x_1$から$x_2$まで定積分する（つまりその範囲で面積を計算する）」を式では$\int_{x_1}^{x_2} f({x})\mathrm dx$と書く。$f({x})$は「被積分関数」と呼ぶ。また、この時の変数は「積分変数」と呼ぶ。
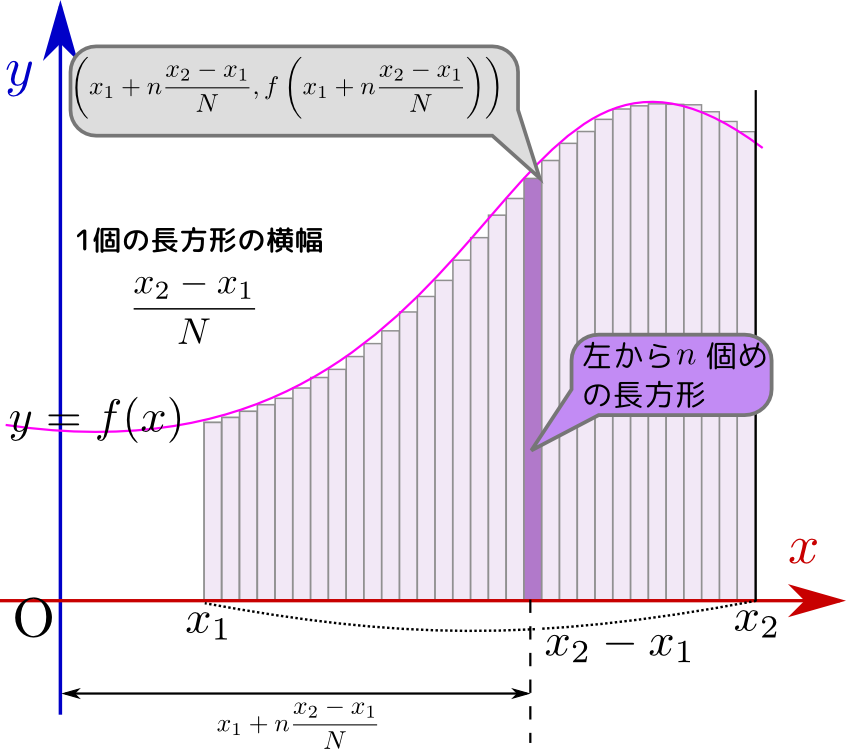
具体的には「$x_1$から$x_2$まで」という長さ$x_2-x_1$の領域を$N$分割しこの分割の方法は、極限をうまく取ることができるような分割でありさえすればよく、${x_2-x_1\over N}$ごとに等分割する方法が唯一ではない（\ref{JacksonInt}節を参照）。ここでは一番単純な分割方法で説明している。、その一個一個の微小領域（最初を「0番目」として、$n$番目の微小領域は${x}=x_1+n{x_2-x_1\over N}$で始まる）に横${x_2-x_1\over N}$で縦$f\left(x_1+ n{x_2-x_1\over N}\right)$の微小長方形を作り、その面積の和を計算する。式で表現すれば
\begin{equation} \int_{x_1}^{x_2} f({x})\mathrm dx = \underbrace{\lim_{N\to\infty}\sum_{n=0}^{N-1} }_{\int_{x_1}^{x_2}} \underbrace{f\left(x_1 + {x_1-x_2\over N} n\right)}_{f({x})}\underbrace{{x_2-x_1\over N}}_{\mathrm dx} \end{equation}ということである。正確には、上に書いたような単純な極限ではなく、「下からの極限」と「上からの極限」になるようにしてから両方を計算した上で二つの極限が一致することを示さなくてはいけない。一致しない場合は「積分可能でない」関数だということになる。
積分を式で書くとき、$\mathrm dx$の位置は$\int_a^bf({x})\mathrm dx$のように後でもいいし、$\int_a^b\mathrm dx f({x})$のように積分記号の直後でもよい。意味は変わらない（微小長方形の面積を$(縦)\times(横)$と書いても$(横)\times(縦)$と書いても問題ないのと同じ）。
$f({x})=AB$のような場合に$\int_a^b \mathrm dx AB$と書くと$AB$を積分しているのか、$A$を積分した後で$B$を掛けるのかわかりにくくなる、という難点があるので$\int_a^b AB \mathrm dx$と書いた方がよいという考え方もできる。一方、$\int_a^b \mathrm dx AB$と書いた方が「積分の上限・下限」という情報と「どの変数で積分しているか」という情報が近い場所にあってよい今の段階ではあまりメリットがないように思えるかもしれないが、後で「重積分」つまり「積分した後で別の変数でまた積分」のようなことをやる時は、$\int_{a}^{b}\mathrm dx \int_c^d \mathrm dy f({x},{y})$のような書き方の方が便利である。という考え方もできる。
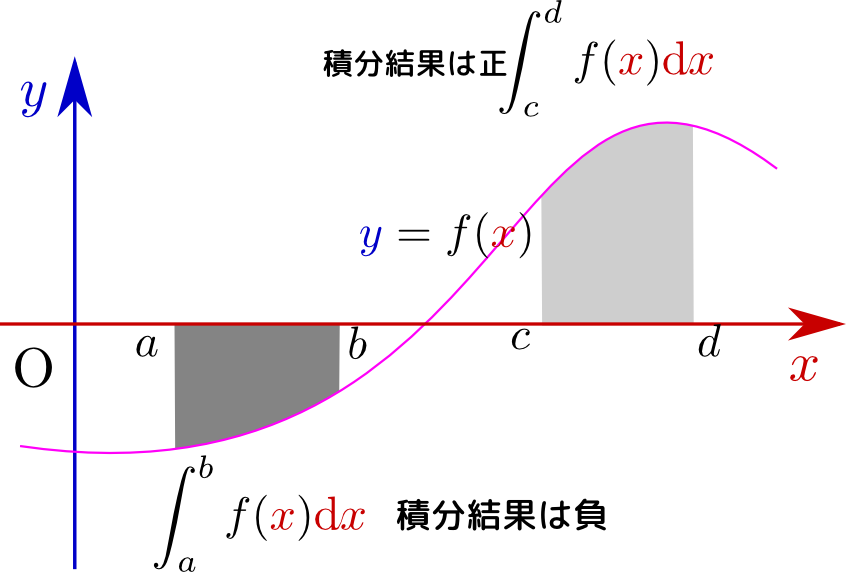
この定義からわかるように、$f({x})$が負の領域での積分はマイナスの値になる。つまり定積分の結果は単純に面積ではなく「$x$軸より下に来ていたら負にして計算する面積」である。
「いやそれは困る。面積は正であって欲しい」という人は、絶対値記号を使って$\int \left|f({x})\right|\mathrm dx$を計算すればよい（実際の計算においては$f({x})$の正負に応じて場合分けが必要になるだろう）。
また、定積分の意味するところから明らかではあるが、
\begin{equation} \int_a^b f({x})\mathrm dx + \int_b^c f({x})\mathrm dx = \int_a^c f({x})\mathrm dx\label{intsum} \end{equation} という式が成立する。これは${x}$の積分の場合だけでなく、全ての関数の定積分で成立する。また、 \begin{equation} \int_a^b f({x})\mathrm dx =- \int_b^a f({x})\mathrm dx \label{hantaiint} \end{equation}すなわち、「上限と下限を取り替えると符号がひっくり返る」という性質元々の「面積を計算したい」という動機だけから考えると、$a< b$の時に$\int_b^a f({x})\mathrm dx$を考えるのはナンセンスに思えるかもしれない。しかし、数式を書く上での規則は、できる限り「例外がない」ものが望ましいので、イレギュラーに見える式も作っておけば後で役立つ（かもしれない）。も持つ。
この式を導くには、「二つ上の式はどのような$a,b,c$でも成立する式であるべきだ」これも「できる限り例外がない規則」が欲しいからである。と考えた上で$c=a$を代入すればよい。すると右辺に出てくる$ \int_a^a f({x})\mathrm dx$が0になることから上の式が導ける。これらを合わせて
\begin{equation} \int_a^c f({x})\mathrm dx - \int_a^b f({x})\mathrm dx = \int_b^c f({x})\mathrm dx\label{hikisanint} \end{equation}という式を作ることもできる（上の図をもう一度よく見るとわかる）。これを使うと、
\begin{equation} \int_{x_1}^{x_2}{x}\mathrm dx = \int_{0}^{x_2}{x} \mathrm dx - \int_{0}^{x_1}{x} \mathrm dx ={(x_2)^2\over 2}-{(x_1)^2\over 2} \end{equation}のように、$\int^{x_1}_0{x}\mathrm dx$がわかれば任意の範囲での定積分を計算することができることになる。
また、微分同様、定積分も線型性を持つ。すなわち、
が成立する。
次に、放物線（ ${y}={x}^2$のグラフ）の下の面積を計算してみよう。同様に$0<{x}< x_0$という範囲を考えることにして、その領域を$N$分割して、微小長さ$\mathrm dx={x_0\over N}$ごとに分けて、その微小長さを横、高さを${y}={x}^2$として作られる長方形の面積をどんどん足していくことにする（下の図参照）。
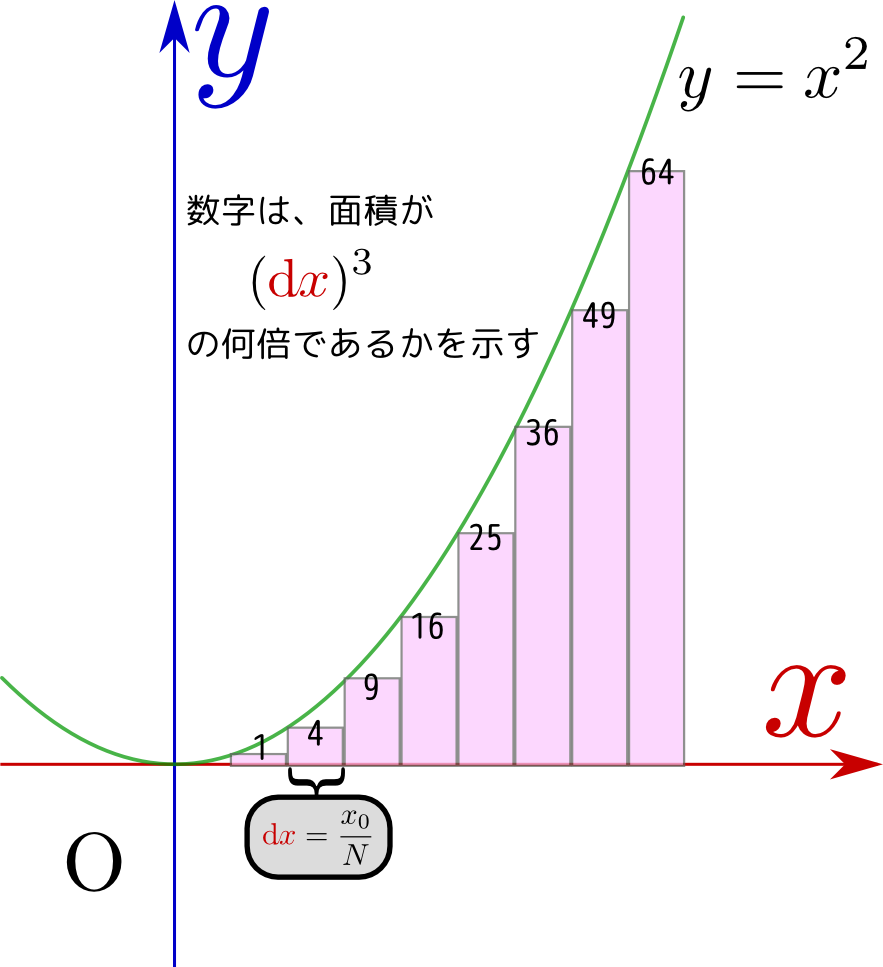
$n$番目の長方形の縦の長さは$\left(n\times{x_0\over N}\right)^2$で横が${x_0\over N}$だから、この二つを掛けた答えである$n^2{(x_0)^3\over N^3}$を$n=1$から$n=N-1$まで足すという計算を行う。結果は
\begin{equation} \sum_{n=1}^{N-1}n^2{(x_0)^3\over N^3} ={(x_0)^3\over N^3}\underbrace{\sum_{n=1}^{N-1}n^2}_{{N(N-1)(2N-1)\over 6}} =(x_0)^3\times{(N-1)(2N-1)\over 6N^2}\label{NNNN} \end{equation}となる。途中で$\sum_{n=1}^{N-1}n^2={N(N-1)(2N-1)\over 6}$という公式を使っている。最後にある${(N-1)(2N-1)\over 6N^2}$は$N\to\infty$で${1\over 3}$に収束するから、今考えている面積は${(x_0)^3\over 3}$へと収束する。前節同様、今求めた面積（「下からの極限」）は求めたい面積より少し小さいが、「上からの極限」を考えると今求めたより少し大きい面積がやはり${(x_0)^3\over 3}$へ収束することがわかるので、
\begin{equation} \int_0^{x_0}{x}^2\mathrm dx={(x_0)^3\over 3}\label{sekibunxsq} \end{equation}が求められたことになる。ここで求めたのは「$0$から$x_0$まで」だが、ここまでやっておけば、任意の範囲についての積分は
\begin{equation} \int_{x_1}^{x_2}{x}^2\mathrm dx = \int_{x_2}^{0}{x}^2\mathrm dx - \int_{x_1}^{0}{x}^2\mathrm dx={(x_2)^3\over 3}-{(x_1)^3\over 3} \end{equation}のように計算できる。
「では次に${x}^3$を」と行きたいところだが、この方法はいずれ行き詰まる。というのは、$\sum_{n=1}^{N-1}n={N(N-1)\over 2},\sum_{n=1}n^2={N(N-1)(2N-1)\over 6}$などの式を使ってきたが、その次の$\sum_{n=1}^{N-1}n^3={N^2(N-1)^2\over 4}$あたりからは知らない人も多いだろうもちろんそういう時は公式集を持ってくればよい。たくさんの公式を全部覚えておく必要などないのである。ただ「こういう公式がある」ということを知りもしないと公式集を引くこともできないから、いろいろな式があることを知っておくべきなのはもちろんのことである。。それに$x^{1.3}$のような整数べきでない場合はもっと難しそうだ。
そこでここでは分割の方法を変え、等分割ではなく「等比数列で分割する」ことで面積を計算する方法を示すこの方法は「ジャクソン積分」と呼ばれている。。例として、$\int_a^b {x}^\alpha\mathrm dx$の積分を行ってみよう。
まず${x}=a$から${x}=b$までの区間を分割するのだが、はじめの分割を$a$から$ar$まで（これを「0番目の分割」とする）としたら、次の分割は$ar$から$ar^2$まで（これが「1番目の分割」）、その次を$ar^2$から$ar^3$（「2番目の分割」）というふうに、$a$を$r^n$倍にした点を区間の区切りにする。
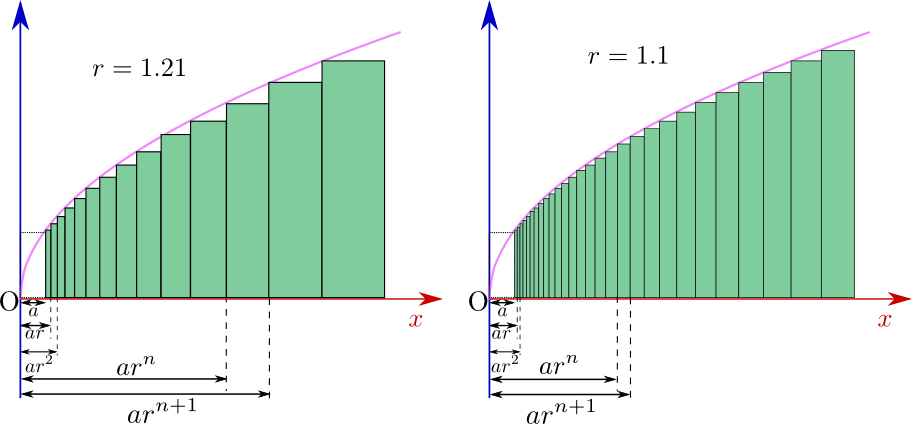
$n$番目の分割の区間は${x}=ar^{n}$から${x}=ar^{n+1}$までである。$r$は1より大きい数で後で1に近づけることで、区間の長さ$ar^{n+1}-ar^{n}$が0に近づく。$N-1$番目の分割で区間の上端が${x}=ar^N$に達するから、$b=ar^N$としておこう。最後に、$r\to1$にするが、このとき$b=ar^N$という関係を保ったまま$r\to1$にする。つまり$N=\log_r\left(b\over a\right)$ということであり、この式から、$r\to1$で$N\to\infty$となる。
上のグラフは$f({x})=\sqrt{{x}}$の場合で描いた。$r$を1に近づけていくことで長方形の面積の和が計算したい部分の面積に近づく。もちろん確認のためには本来は図に示したような「下からの極限」だけではなく「上からの極限」も考えて挟み撃ちにすべきである（ここでは省略する）。
$n$番目の分割の区間で作られる長方形の高さは$(ar^n)^\alpha$である。一方長方形の幅は、$ar^{n+1}$から$ar^n$を引けばよいので、$ar^n(r-1)$となる。0番目から$N-1$番目までを足算して全長方形の面積の和を求めると
\begin{equation} \sum_{n=0}^{N-1} ar^n(r-1)\times (ar^n)^\alpha=a^{\alpha+1} (r-1)\sum_{n=0}^{N-1}r^{n(\alpha+1)} \end{equation}となるが、等比級数の和の公式から、$\sum_{n=0}^{N-1}r^{n(\alpha+1)}={1-r^{N(\alpha+1)}\over 1-r^{\alpha+1}}$であるから、求めるべき量は
\begin{equation} a^{\alpha+1} (r-1)\times{1-r^{N(\alpha+1)}\over 1-r^{\alpha+1}} = \left( a^{\alpha+1}-(ar^N)^{\alpha+1} \right)\times{r-1\over 1-r^{\alpha+1}} \end{equation}である。ここで$b=ar^N$だったから、この量は
\begin{equation} \left( b^{\alpha+1}-a^{\alpha+1} \right)\times{1-r\over 1-r^{\alpha+1}} \end{equation}である。後半部を考えよう。$r$は1に近づく量だから、$r=1+h$と置くと、$h$が0に近づく量である。微分の時に冪乗を展開した時の考え方を使って
\begin{equation} r^{\alpha+1}=(1+h)^{\alpha+1}=1+(\alpha+1)h+{\cal O}(h^2) \end{equation}と書き換えられるので、
\begin{equation} \lim_{h\to0}{1-(\overbrace{1+h}^r)\over 1-(\underbrace{1+h}_r)^{\alpha+1}} = \lim_{h\to0}{-h\over 1-(1+(\alpha+1)h)} =\lim_{h\to0}{-h\over -(\alpha+1)h} ={1\over \alpha+1} \end{equation}のように極限値が求められる。
結論は、
\begin{equation} \int_a^b{x}^\alpha \mathrm dx = {b^{\alpha+1}\over \alpha+1}-{a^{\alpha+1}\over \alpha+1} \end{equation}である。たいへんありがたいことに、この式の$\alpha$は$-1$以外ならどんな実数でもよい。この式で、$a=0,b=x_0$と置く。$\alpha+1>0$のときならば$\lim_{a\to0}a^{\alpha+1}=0$なので、
\begin{equation} \int_0^{x_0}{x}^\alpha \mathrm dx = {(x_0)^{\alpha+1}\over \alpha+1}\label{intxalpha} \end{equation}となり、$\alpha=1,2$の時にはこれまで計算してきた${x}$の積分と${x}^2$の積分に一致する。
ここまでの計算でわかった、定積分における${x}^\alpha\to {(x_0)^{\alpha+1}\over \alpha+1}$という対応関係が、微分における${x}^\alpha \to \alpha {x}^{\alpha-1}$（あるいは、この$\alpha$を一つずらした${x}^{\alpha+1}\to (\alpha+1){x}^\alpha$の方がわかりやすい）という対応関係を比較してみよう。
この二つが「逆」であることに気づいたろうか（冪が$\alpha\to\alpha+1$と上がるか$\alpha+1\to\alpha$と下がるか、係数は$\alpha+1$を掛けるか、$\alpha+1$で割るか）。そのつながりこそが次の「微積分学の基本定理」のエッセンスである。