空間座標と偏微分
2次元の直交座標と極座標
今日はまず、直交座標・極座標と偏微分の関係から。
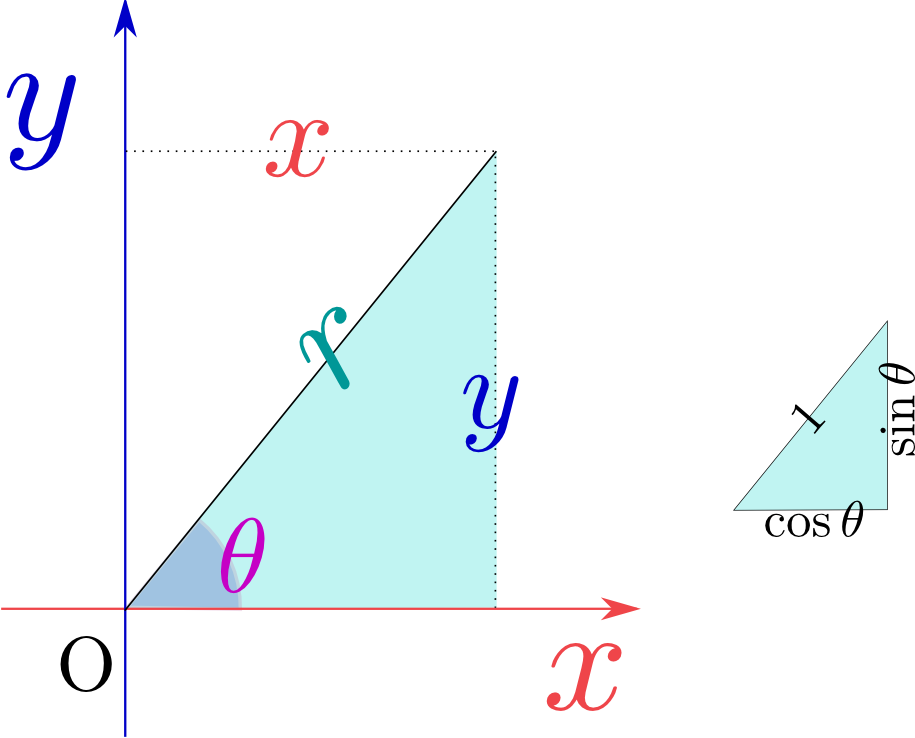
2次元の位置を表現するのによく使われるのは直交座標(デカルト座標)で、${x},{y}$の二つを使って位置を表現する。もう一つよく使われるのが極座標で、これは原点からの距離${r}(=\sqrt{{x}^2+{y}^2})$と、どの方向に原点から離れているかを意味する${\theta}$で位置を表現するその意味からして、${r}=0$(原点)では座標${\theta}$は無意味になることに注意。。図からわかるように、
\begin{equation} \begin{array}{ccccc} {x}={r}\cos {\theta}&,&{y}={r}\sin {\theta}&,&\\ \cos{\theta}={{x}\over \sqrt{{x}^2+{y}^2}}&,&\sin{\theta}={{y}\over \sqrt{{x}^2+{y}^2}}&,&{r}=\sqrt{{x}^2+{y}^2} \end{array} \end{equation}という関係がある。
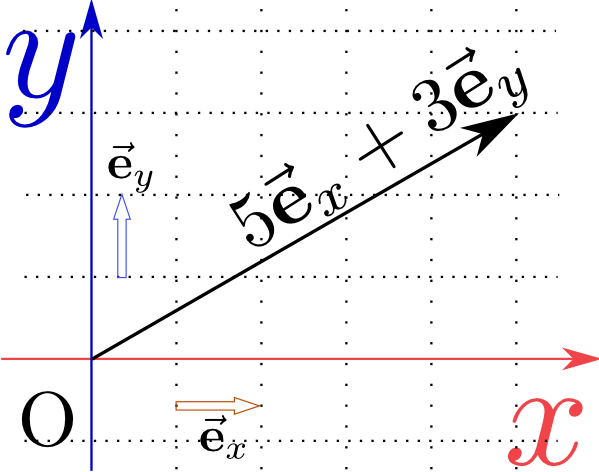
直交座標で${x}$軸方向を向いた単位ベクトル(長さが1のベクトルのこと)を$\vec{\mathbf e}_x$、${y}$軸方向を向いた単位ベクトルを$\vec{\mathbf e}_y$と書くことにする。すると位置ベクトル(原点から場所$({x},{y})$へ引いた矢印のベクトル)は$\vec x={x}\vec{\mathbf e}_x+{y}\vec{\mathbf e}_y$のように書くことができる(この書き方と、成分を並べて$({x},{y})$と書くのは全く同じ意味)。
極座標でも$r$方向($r$が増加する方向)の単位ベクトル、$\theta$方向($\theta$が増加する方向)の単位ベクトルを考えて、これを$\vec{\mathbf e}_r,\vec{\mathbf e}_\theta$と書く(${\bf \hat r},{\bf \hat \theta}$と書いている本もある)。図に表したように(そして、その定義から当然そうなるべく)、$\vec{\mathbf e}_r,\vec{\mathbf e}_\theta$は場所によって違う方向を向く原点においては、$\vec{\mathbf e}_r,\vec{\mathbf e}_\theta$ともに定義できない。原点は極座標の「特異点」である。。
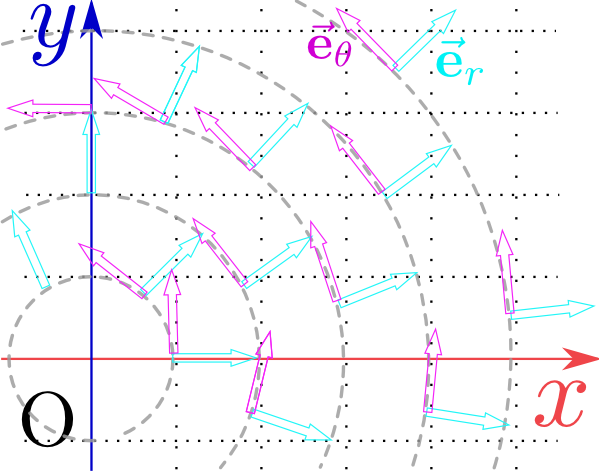
$\vec{\mathbf e}_r=(\cos \theta,\sin \theta)$であり、それと直交する$\vec{\mathbf e}_\theta$は$(-\sin \theta,\cos \theta)$である$\vec{\mathbf e}_r=\cos\theta\vec{\mathbf e}_x+\sin\theta\vec{\mathbf e}_y,\vec{\mathbf e}_\theta=-\sin\theta\vec{\mathbf e}_x+\cos\theta\vec{\mathbf e}_y$と書いても同じこと。。よって、${r}$方向の偏微分は
\begin{equation} \vec{\mathbf e}_r\cdot({\rm grad}~f)= \cos \theta{\partial f({x},{y})\over \partial x}+\sin \theta{\partial f({x},{y})\over \partial y}\label{rhoukou} \end{equation}となる。同様に${\theta}$方向の偏微分は
\begin{equation} \vec{\mathbf e}_\theta\cdot({\rm grad}~f)= -\sin \theta{\partial f({x},{y})\over \partial x}+\cos \theta{\partial f({x},{y})\over \partial y}\label{thetahoukou} \end{equation}となる。上の式は${r}$微分に一致するが、下の式の方は${\theta}$微分と一致しない。これらのことを以下で確認しよう。
座標変換による偏微分の変換
直交座標で考えた関数$f({x},{y})$を、極座標で書き直す。その結果である関数$g({r},{\theta})$は、
\begin{equation} f({x},{y})\biggr|_{{x}={r}\cos {\theta},\atop {y}={r}\sin {\theta}}=g({r},{\theta}) \end{equation}と書くことができる。$f({x},{y})$の${x}$に${r}\cos {\theta}$を、${y}$に${r}\sin {\theta}$を代入した結果が$g({r},{\theta})$である。これを、
\begin{equation} f\bigl( {x}({r},{\theta}),{y}({r},{\theta}) \bigr)=g({r},{\theta})\label{fxyrtheta} \end{equation}と表現してもよい。つまり、${r},{\theta}$を決めると${x}({r},{\theta})$と${y}({r},{\theta})$が決まり、それによって$f$の値が決まる(よって上の式$x,y$は「関数の名前」であって変数ではない)。これを(${\theta}$を一定として)${r}$で微分する。その意味するところは、
\begin{equation} \left( {\partial f\bigl( x({r},{\theta}),y({r},{\theta}) \bigr)\over \partial r} \right)_{\!\!{\theta}} =\lim_{{\Delta r}\to0} { f\bigl( x({r}+{\Delta r},{\theta}),y({r}+{\Delta r},{\theta}) \bigr) -f\bigl( x({r},{\theta}),y({r},{\theta}) \bigr) \over {\Delta r} }\label{delfdelr} \end{equation}である。ここで、
\begin{equation} \begin{array}{rl} x({r}+{\Delta r},{\theta})=&x({r},{\theta}) +{\partial x({r},{\theta})\over \partial r}{\Delta r}\\[3mm] y({r}+{\Delta r},{\theta})=&y({r},{\theta}) +{\partial y({r},{\theta})\over \partial r}{\Delta r} \end{array} \end{equation}を使うと、上の式の右辺の分子が
\begin{equation} f\bigl( x({r},{\theta})+{\partial x({r},{\theta})\over \partial r}{\Delta r},y({r}+{\partial y({r},{\theta})\over \partial r}{\Delta r},{\theta}) \bigr) -f\bigl( x({r},{\theta}),y({r},{\theta}) \bigr) \end{equation}と書ける。$f({x}+{\Delta x},{y}+{\Delta y})=f({x},{y})+{\partial f\over \partial x}{\Delta x}+{\partial f\over \partial y}{\Delta y}$と同様に、第1項を${\Delta r}$の1次まで展開すれば
\begin{equation} f\bigl( x({r},{\theta}),y({r},{\theta}) \bigr) +\overbrace{{\partial f(x,y)\over \partial x}\underbrace{{\partial x({r},{\theta})\over \partial r}{\Delta r}}_{{\Delta x}}}^{xの変化による部分} +\overbrace{{\partial f(x,y)\over \partial y}\underbrace{{\partial y({r},{\theta})\over \partial r}{\Delta r}}_{{\Delta y}}}^{yの変化による部分} \end{equation}のようになる(${\cal O}(({\Delta r})^2)$は省略)から、引算を実行した結果を${\Delta r}$で割ることにより、
\begin{equation} {\partial f\bigl( x({r},{\theta}),y({r},{\theta}) \bigr)\over \partial r} ={\partial f(x,y)\over \partial x}{\partial x({r},{\theta})\over \partial r} +{\partial f(x,y)\over \partial y}{\partial y({r},{\theta})\over \partial r}\label{delfdelrkekka} \end{equation}となる。
ここで、$x({r},{\theta})={r}\cos {\theta},y({r},{\theta})={r}\sin {\theta}$であることから、
\begin{equation} {\partial x({r},{\theta})\over \partial r}=\cos{\theta},~~ {\partial y({r},{\theta})\over \partial r}=\sin{\theta}\label{delxdelr} \end{equation}である。ゆえに、確かに${r}$方向の方向微分である$\left(\vec{\mathbf e}_r\cdot({\rm grad}~f)={\partial f\over \partial r}\right)$。
${\theta}$による偏微分を行うと、
\begin{equation} \begin{array}{rl} {\partial f\bigl( x({r},{\theta}),y({r},{\theta}) \bigr)\over \partial \theta} =&{\partial f(x,y)\over \partial x}{\partial x({r},{\theta})\over \partial \theta} +{\partial f(x,y)\over \partial y}{\partial y({r},{\theta})\over \partial \theta}\\ =&\underbrace{-r\sin \theta}_{{\partial x({r},{\theta})\over \partial \theta} }{\partial f(x,y)\over \partial x} +\underbrace{r\cos \theta}_{{\partial y({r},{\theta})\over \partial \theta}}{\partial f(x,y)\over \partial y} \end{array}\label{delthetatheta} \end{equation}となり、${\theta}$方向の方向微分とは、${r}$倍違う$\left(\vec{\mathbf e}_\theta\cdot({\rm grad}~f)={1\over r}{\partial f\over \partial\theta}\right)$。
変数を変更した時の偏微分の変化
前節では$({x},{y})$から$({r},{\theta})$へと独立変数の組を変えるという操作を行った。一般的に、独立変数の組を変更した時、偏微分がどのように変化するかを示そう。
2変数の一般的変数変換
$({x},{y})$から$({X},{Y})$へと変数を変える。もちろん、${X},{Y}$は両方とも${x},{y}$の関数である。省略せずに書けば$g\left({X}({x},{y}),{Y}({x},{y})\right)$ということになる。
\begin{equation} f({x},{y})=g\left({X}({x},{y}),{Y}({x},{y})\right) \end{equation}とする。この式の両辺を${x}$で偏微分する(つまり${y}$を一定として微分を行う)。定義どおりに計算すると、
\begin{equation} \begin{array}{rl} &\lim_{{\Delta x}\to0} { f({x}+{\Delta x},{y})-f({x},{y}) \over {\Delta x}}\\ =&\lim_{{\Delta x}\to0}{ g\left({X}({x}+{\Delta x},{y}),{Y}({x}+{\Delta x},{y})\right) -g\left({X}({x},{y}),{Y}({x},{y})\right) \over {\Delta x} } \end{array} \end{equation}となり、前節同様の計算を行えば、
\begin{equation} \left({\partial f({x},{y})\over \partial x}\right)_{\!\!{y}}= \left( {\partial g({X},{Y})\over \partial X}\right)_{\!\! Y} \left( {\partial {X}({x},{y})\over \partial x}\right)_{\!\!{y}} +\left( {\partial g({X},{Y})\over \partial Y}\right)_{\!\! X} \left( {\partial {Y}({x},{y})\over \partial x}\right)_{\!\!{y}}\label{ippanhenbibunhenkan} \end{equation}となる。同様に計算して、
\begin{equation} \left({\partial f({x},{y})\over \partial y}\right)_{\!\!{x}}= \left( {\partial g({X},{Y})\over \partial X}\right)_{\!\! Y} \left( {\partial {X}({x},{y})\over \partial y}\right)_{\!\!{x}} +\left( {\partial g({X},{Y})\over \partial Y}\right)_{\!\! X} \left( {\partial {Y}({x},{y})\over \partial y}\right)_{\!\!{x}}\label{ippanhenbibunhenkantwo} \end{equation}である。
より一般的に、${x}_1,{x}_2,\cdots,{x}_N$という$N$-変数の組から${X}_1,{X}_2,\cdots,{X}_N$という変数の組へと変更する時には、
多変数関数の変数変換
\begin{equation} \begin{array}{rl} & \left( {\partial f({x}_1,{x}_2,\cdots,{x}_N)\over \partial x_i}\right)_{\!\!{x}_i以外の{x}} \\ =&\sum_{j=1}^N\left( {\partial \tilde f({X}_1,{X}_2,\cdots,{X}_N)\over \partial X_j} \right)_{\!\!{X}_i以外の{X}}\left({\partial X_j({x}_1,{x}_2,\cdots,{x}_N)\over \partial x_i}\right)_{\!\!{x}_i以外の{x}} \end{array} \end{equation}およびこの逆
\begin{equation} \begin{array}{rl} & \left( {\partial \tilde f({X}_1,{X}_2,\cdots,{X}_N)\over \partial X_i}\right)_{\!\!{X}_i以外の{X}} \\ =&\sum_{j=1}^N\left( {\partial f({x}_1,{x}_2,\cdots,{x}_N)\over \partial x_j} \right)_{\!\!{x}_i以外の{x}}\left({\partial x_j({X}_1,{X}_2,\cdots,{X}_N)\over \partial X_i}\right)_{\!\!{X}_i以外の{X}} \end{array} \end{equation}が成立する。
偏微分の注意点
偏微分の計算を行うときに有用な公式と、誤りやすい注意点を述べておく。
よくある誤り
${\partial x\over \partial r}=\cos\theta$だから、${\partial r\over \partial x}={1\over \cos\theta}$だろう。常微分であれば、${\mathrm dy\over \mathrm dx}={1\over {\mathrm dx\over \mathrm dy}}$は成立するので、ついこうだろうと思ってしまうかもしれない。しかし実際に${\partial r\over \partial x}$を計算してみよう。${x},{y}$を独立変数として$r$はその関数$r({x},{y})=\sqrt{{x}^2+{y}^2}$と見る。これを${x}$で偏微分すると、
\begin{equation} {\partial \left(\sqrt{{x}^2+{y}^2}\right)\over \partial x} = {1\over 2\sqrt{{x}^2+{y}^2}}\times 2{x}={{x}\over \sqrt{{x}^2+{y}^2}}=\cos\theta \end{equation}となり、${1\over \cos\theta}$にはならない。一方で、${r},{\theta}$を独立変数として$x$を$x({r},{\theta})={r}\cos{\theta}$と考えれば、
\begin{equation} {\partial \left({r}\cos{\theta}\right)\over \partial r}=\cos{\theta} \end{equation}となる。
うっかりと、${\partial x\over \partial r}={1\over {\partial r\over \partial x}}$のように思ってしまうのは、記号を省略した記法を使っているからである。省略せずに書くと、${\partial x\over \partial r}$は$\left({\partial x({r},{\theta})\over \partial r}\right)_{\!\!{\theta}}$であり、${\partial r\over \partial x}$は$\left({\partial r({x},{y})\over \partial x}\right)_{\!\!{y}}$である。大事なことは変数の取り方の違いである。特に「どの変数を固定して微分しているか」が違う点に注意しなくてはいけない。
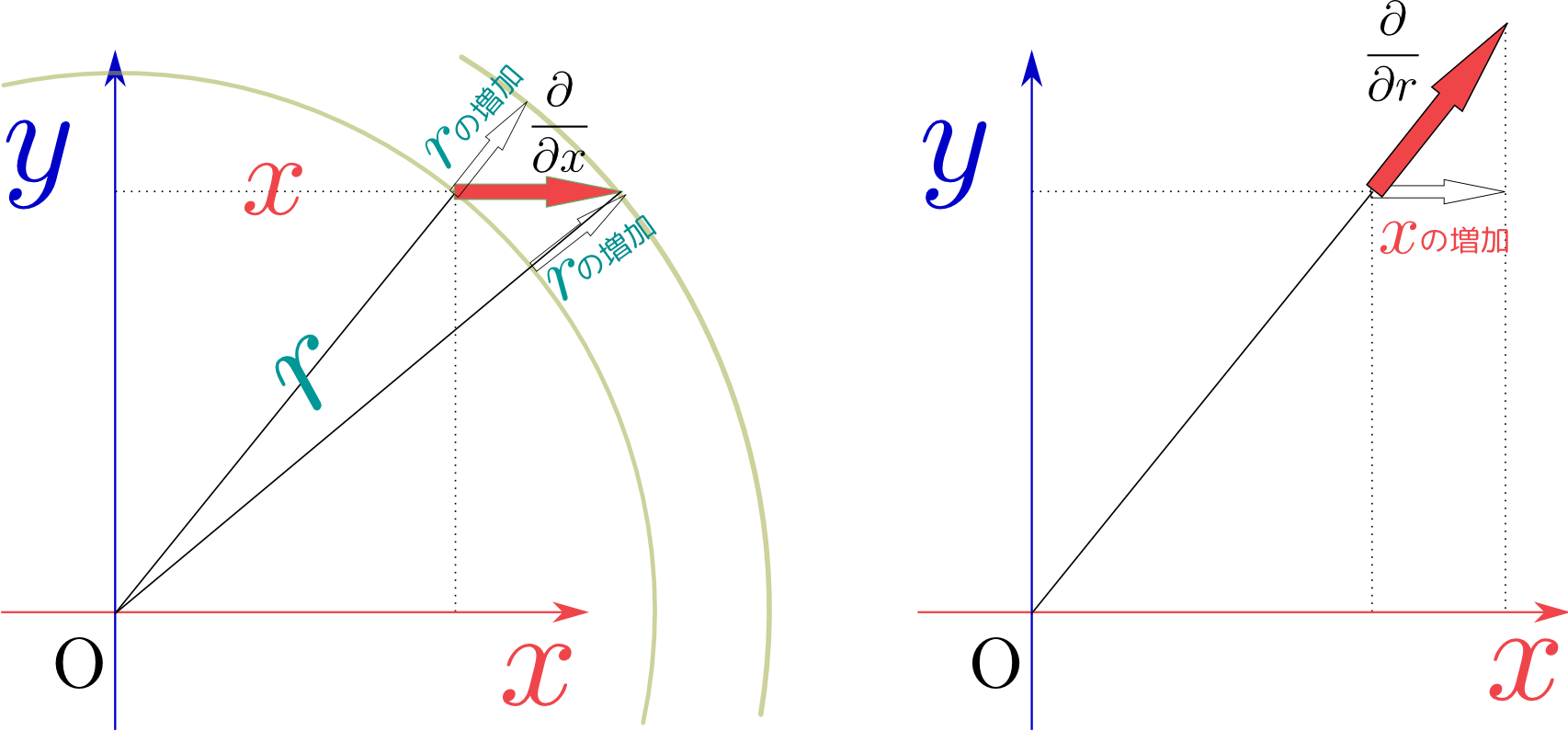
逆に「どの変数を固定しているのか」が同じであれば、常微分のときと同様に${\partial r\over \partial x}={1\over {\partial x\over \partial r}}$が成立する。${y}$を一定とすることにすれば、
\begin{equation} \left( {\partial r\over \partial x}\right)_{\!\!{y}} = {1\over \left( {\partial x\over \partial r}\right)_{\!\!{y}}} \end{equation}である。確認しよう。左辺は
\begin{equation} \left( {\partial \sqrt{{x}^2+{y}^2}\over \partial x}\right)_{\!\!{y}} ={{x}\over \sqrt{{x}^2+{y}^2}}={{x}\over {r}} \end{equation}右辺の分母は、${r}$と${y}$を変数と考えての微分だから、${x}=\pm\sqrt{{r}^2-{y}^2}$として、
\begin{equation} \pm\left({\partial \sqrt{{r}^2-{y}^2}\over \partial r}\right)_{\!\!{y}} =\pm{{r}\over\sqrt{{r}^2-{y}^2} }={{r}\over {x}} \end{equation}となり、確かにこの二つは逆数である。
よくある誤り
常微分の時に${\mathrm dz\over \mathrm dy}{\mathrm dy\over \mathrm dx}={\mathrm dz\over \mathrm dx}$ができたのだから偏微分でも${\partial z\over \partial y}{\partial y\over \partial x}={\partial z\over \partial x}$だろう。
これも、省略記法で書いているせいで「これでいい」と勘違いしてしまうことがある。誤解がないよう省略なしで書くと、常微分は${\mathrm dz(x)\over \mathrm dy}{\mathrm dy(x)\over \mathrm dx}={\mathrm dz(y(x))\over \mathrm dx}$である一方偏微分は$\left({\partial z(x,y)\over \partial y}\right)_{\!\!x}\left({\partial x(y,z)\over \partial z}\right)_{\!\!y}\left({\partial y(z,x)\over \partial x}\right)_{\!\!z}$であり、本質的に違う計算なのである常微分の方では「$x$が決まると$y$が決まり、次に$z$が決まる」という関係、偏微分の方は「$x$と$y$が決まると$z$が決まる(あるいはこの立場入れ替え)」という関係を保ちつつ変化量の計算(微分)が行われる。。
例として、${x}^2+{y}^2+{z}^2=R^2$が成り立つ(つまり、3次元の球面の上に$({x},{y},{z})$がある)場合を考えよう。この場合${z}=\pm\sqrt{R^2-{x}^2-{y}^2}$とか${y}=\pm\sqrt{R^2-{x}^2-{z}^2}$のような関係式がある。複号があると考えるのが面倒なので、考える範囲を${x},{y},{z}$が全て正である領域に限ろう。すると複号は全て正になる。微分を実行すると、
\begin{equation} \left({\partial z({x},{y})\over \partial y}\right)_{\!\!{x}} =- {{y}\over \sqrt{R^2-{x}^2-{y}^2}},~~~~ \left({\partial y({x},{z})\over \partial x}\right)_{\!\!{z}} =- {{x}\over \sqrt{R^2-{x}^2-{z}^2}} \end{equation}である。この二つの掛算をし、$\sqrt{R^2-{x}^2-{z}^2}={y}$であることを使うと、
\begin{equation} \left({\partial z({x},{y})\over \partial y}\right)_{\!\!{x}} \left({\partial y({x},{z})\over \partial x}\right)_{\!\!{z}} ={{y}\over \sqrt{R^2-{x}^2-{y}^2}}\times{{x}\over \sqrt{R^2-{x}^2-{z}^2}} ={{x} \over \sqrt{R^2-{x}^2-{y}^2}} \end{equation}となる。一方、
\begin{equation} \left({\partial z({x},{y})\over \partial x}\right)_{\!\!{y}} =- {{x}\over \sqrt{R^2-{x}^2-{y}^2}} \end{equation}だから、この二つの式から
\begin{equation} \left({\partial z({x},{y})\over \partial y}\right)_{\!\!{x}} \left({\partial y({x},{z})\over \partial x}\right)_{\!\!{z}} = - \left({\partial z({x},{y})\over \partial x}\right)_{\!\!{y}}\label{henbibunminus} \end{equation}が正しい(右辺のマイナス符号に注意!)。
この式が一般的に正しいことを二通りの方法で示そう。
${x},{y},{z}$という3次元の空間を考えて、ある関係式(上の例では${x}^2+{y}^2+{z}^2=R^2$であった)があることによりこのうち二つが独立であったとする。
関係があるのだから、三つの変数のうち一つを他の二つで表すことができる。そこで
\begin{equation} {x}=X({y},{z}),~ {y}=Y({x},{z}),~ {z}=Z({x},{y}) \end{equation}という三つの式を作ることができたものとしよう。第3の式に第2の式を代入すると、
\begin{equation} {z}=Z\left({x},Y({x},{z})\right)\label{zz} \end{equation}という式ができる。計算の結果、この式は${z}={z}$という当たり前の式に戻る筈である(上の例、${z}=\pm\sqrt{R^2-{x}^2-{y}^2}$と${y}=\pm\sqrt{R^2-{x}^2-{z}^2}$を代入して確認してみよ)。
つまり、この式\式{zz}の右辺は${x}$を含んでいるように見えるが、実は含んでいない(計算をすれば消えてしまう)。ここで、両辺を「${z}$を一定として${x}$で微分」する。計算するまでもなく(${z}$を一定としているのだから)左辺の微分は0である。一方右辺は${x}$が2箇所にあることから微分の結果は二つの式の和となり、結果が0となる(二つの項が打ち消す)。すなわち、
\begin{equation} 0=\left( {\partial z(x,Y)\over \partial x}\right)_{\!\!Y} +\left( {\partial z(x,Y)\over \partial Y}\right)_{\!\!{x}}\left( {\partial Y({x},{z})\over \partial x}\right)_{\!\!{z}} \end{equation}が導かれる。この式は\式{henbibunminus}と同じ式である(移項の際に$-$が出る)。
以上は計算による導出だが、次に図解を試みよう。変数の間の関係式を成立させつつ、三つの変化
- ${x}$を一定として${y}$を変化させる。連動して${z}$が変わる。
- ${y}$を一定として${z}$を変化させる。連動して${x}$が変わる。
- ${z}$を一定として${x}$を変化させる。連動して${y}$が変わる。
を起こして元の場所に戻ってくる経路を考える。
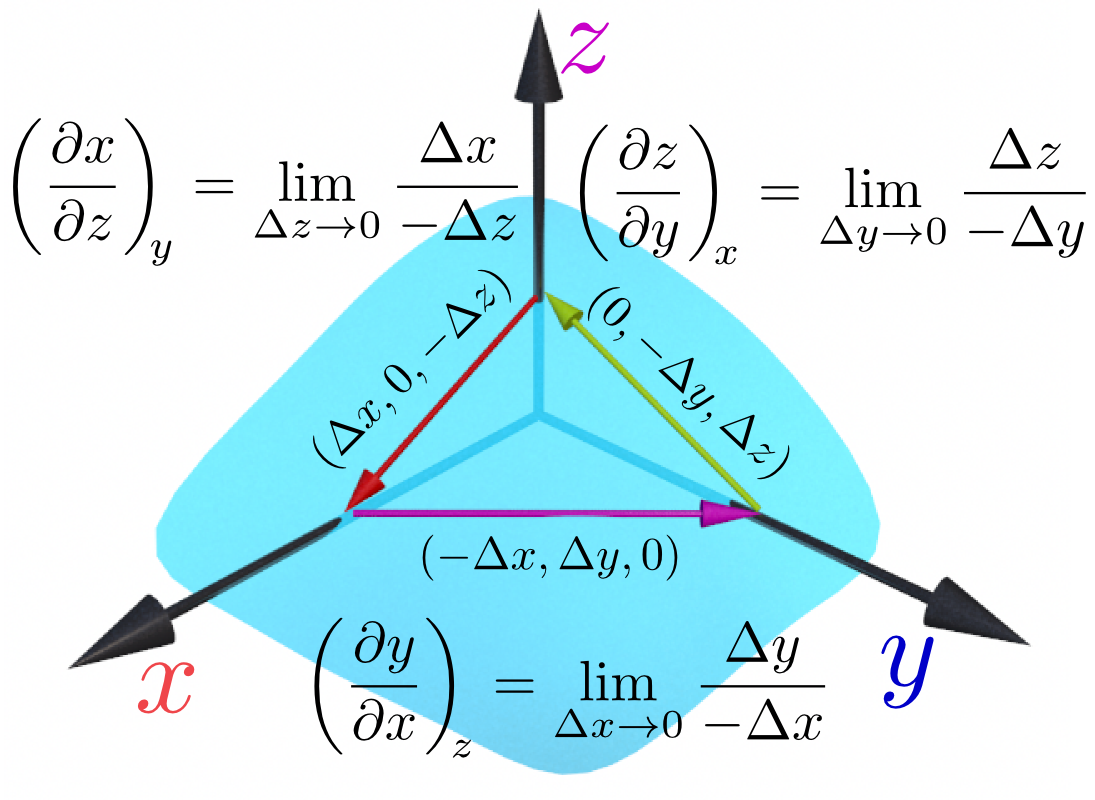
それぞれの過程において図に描き込んだような分数を計算し、その掛算を行うと、
\begin{equation} {\Delta y\over -\Delta z}\times {\Delta z\over -\Delta x}\times {\Delta x\over -\Delta y}=-1 \end{equation}となる(分母分子に同じものが2回ずつ現れ、分母にマイナスが3回現れる)。極限を取ればこれは
\begin{equation} \left({\partial y(x,z)\over \partial x}\right)_{\!\!z}\times \left({\partial z(x,y)\over \partial y}\right)_{\!\!x}\times \left({\partial x(y,z)\over \partial z}\right)_{\!\!y}=-1 \end{equation}になる。ここで、$ \left({\partial x(y,z)\over \partial z}\right)_{\!\!y}={1\over \left({\partial z(x,y)\over \partial x}\right)_{y} }$である(この場合は、同じ変数$y$を固定しての微分だから、逆数になってよい)から、この式は\式{henbibunminus}と同じ式である。
偏微分でも、固定する変数が違わなければマイナス符号は出ない。たとえば$\left({\partial f\over \partial z}\right)_{\!\!x}\times \left({\partial z\over \partial y}\right)_{\!\!x}=\left({\partial f\over \partial y}\right)_{\!\!x}$である。「なぜこうなるのか(符号がつくのか)」という本質を理解すべし。