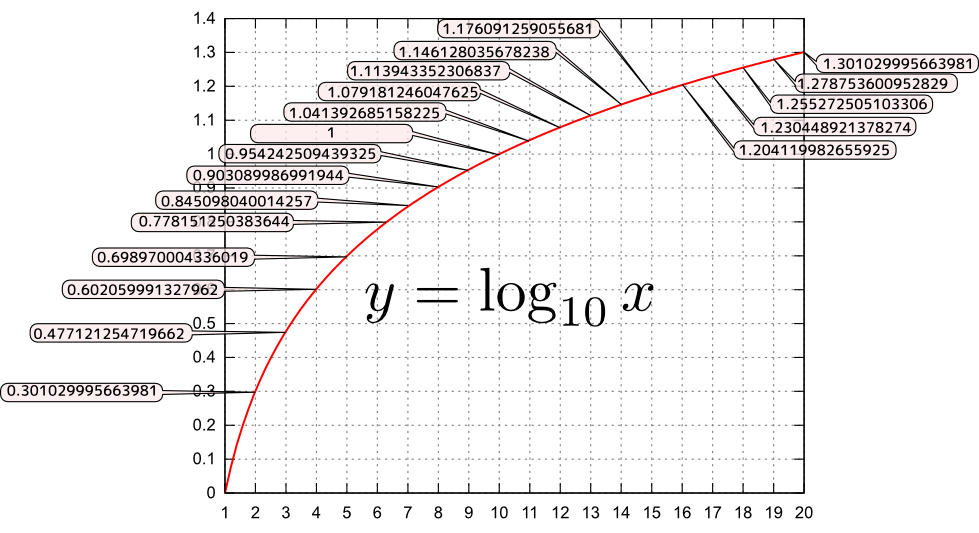
指数関数(続き)
指数関数の傾きとネイピア数
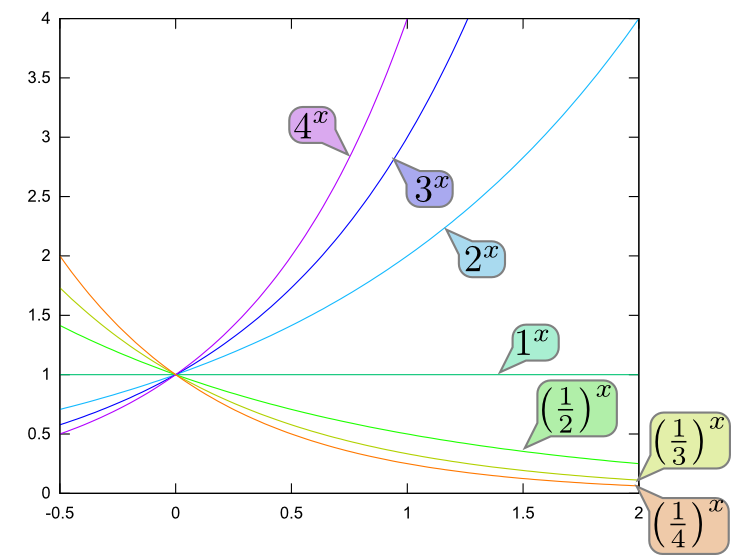
底が大きくなると指数関数は増加の度合いが大きくなる。$a$が1より小さい場合は、むしろ減少する関数となる。
本講義ではここまででも何度か強調しているが、「関数のある点の近傍でのふるまい」を考えることは重要である。そこで指数関数の原点付近でのふるまいを見ておこう。
グラフにも示されているように、$x=0$のときの$y=a^{x}$の値はすべての$a$で等しく1である。一方、$x=0$でのグラフの傾きは、底$a$が大きいほど大きい。そこで、この傾きがちょうど1になるところの$a$を探す。そのときの$a$を e と書いて「ネイピア数(Napier's constant)」もしくは「自然対数の底」と呼ぶ対数とはなにかは、まだ説明してない。言葉の定義の順番が混乱しているのは許して欲しい。。シンプルに e (いー)と呼んでいることも多い変数$e$と区別するために、 e は立体で書く(イタリックにしない)ことにする。。
e の値を知る方法について考えよう。下の図は$y=2^{x}$と$y=3^{x}$と、傾き1で$(0,1)$を通る直線$y=x+1$のグラフである。
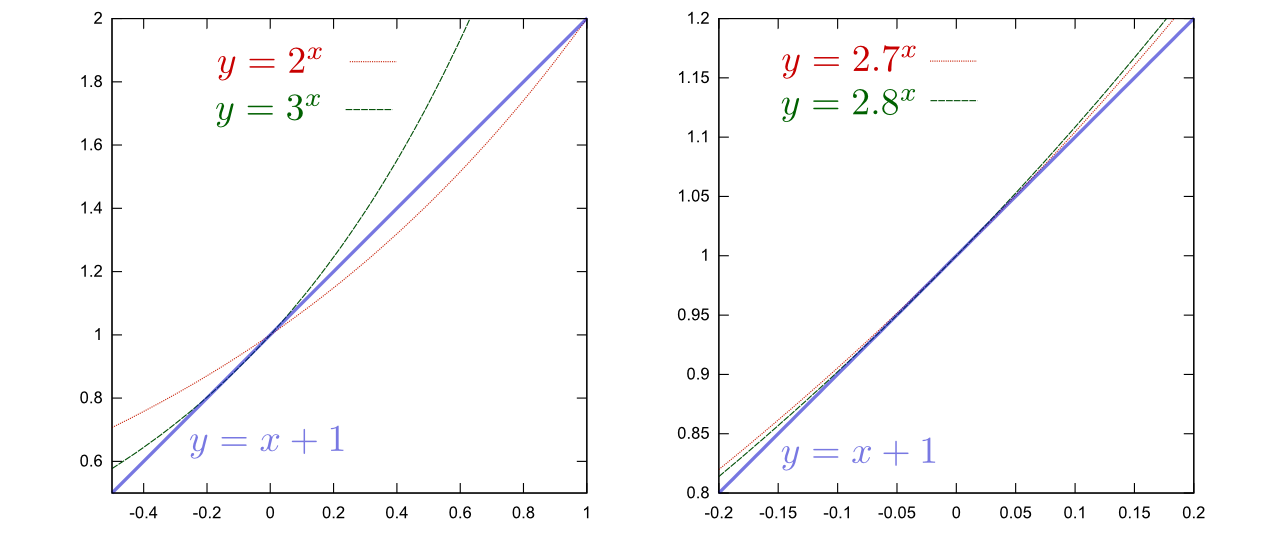
これを見ると、$x=0$で傾き1になるためには、2よりは大きく3よりは小さい数を底にしなくてはいけない。数字をどんどん細かくしていきながら考えていく。たとえば次の段階では、$y=2.7^{x}$と$y=2.8^{x}$のグラフの間に直線$y=x+1$があることから、 e が2.7より大きく2.8より小さいことがわかる。この手続を繰り返すことで、 e の値を精密にしていくことができるだろう(グラフは重なってしまってわかりにくいが)。
下↓のスライダーでaの値を変えられるので、原点での傾きが二つのグラフで一致する場所を探してみよう。
こうやって求めた e の大きさは e=2.718281828459045… である。この e は無理数であることが証明されていて、無限に続く小数である。この値をどうやって計算するのかについては、ここでは「いろんな値を入れてグラフを描いていき、傾きが1になるところを探せば e は計算できるだろう」という程度の大雑把な理解にとどめておこう。実際にはこんな面倒なことはやらない。実際的で、かつ大雑把でない理解のために微分という計算が必要になる。
なぜ傾き1がそんなに大事なのかについては後でわかるが、ここでは「傾きはすなわち微分であり、微分を知ることが自然法則を知る手がかりになる」ということを思い出しておこう。
電卓でeを計算する方法
上のようにして e が計算できる理由は、後で出てくる(だからまだわからなくてもよい)、
\begin{equation} {\mathrm e}^x = 1+x+{x^2\over 2!}+{x^3\over 3!}+{x^4\over 4!}+{x^5\over 5!}+\cdots\label{extenkai} \end{equation}という式(${\mathrm e}^x$のテイラー展開の式)があって、この式に$x=1$を代入すると、
\begin{equation} {\mathrm e} = 1+1+{1\over 2!}+{1\over 3!}+{1\over 4!}+{1\over 5!}+\cdots \end{equation}になるからである。\式{extenkai}がどうやって出てくるかは後のお楽しみであるが、とりあえず${\mathrm e}^{x}=1+x+\cdots$までは「$x=0$での値が1で傾きが1」ということからわかる。
この特別な数字 e を使った指数関数$y={\mathrm e}^{x}$は、「微分方程式を解く」という作業において頻出する。そこでこれを特に、$y=\exp(x)$のように書くこともある。$\exp$は「イクスポーネンシャル」と読む${\mathrm e}^{x}$を「イクスポーネンシャルエックス」のように読むこともある。。
指数関数の底の変換
$y=2^{x}$という関数と$y=4^{{X}}$という関数を考えよう。${X}=2x$ならばこの二つが等しい、すなわち
\begin{equation} 2^{2{X}}= (2^2)^{X}=4^{X} \end{equation}である(たとえば、$2\times 2\times 2\times 2=(2\times 2)\times(2\times 2)=4^2$)。今は2と4という単純な例で考えたが、もっと一般的に$y=a^x$と$y=b^{X}$の関係を考えよう。たとえば、$a$と$b$の間に$a=b^c$($c$もまた別の定数)という関係があるなら、
\begin{equation} a^x= (b^c)^x=b^{cx} \end{equation}となるから、${X}=cx$とすればこの二つの関数が同じ関数になる。
指数関数の底はいろんな値を使ってよいのだが、日常計算においては$y=10^x$のように10が使われることが多い。一方、コンピュータや情報科学の世界では$y=2^x$のように2がよく使われる。
これも後でわかることだが、微分や積分などを行う時には e を底にした指数関数$y={\mathrm e}^x$がもっとも使いやすい。よってこれらを互いに変換する必要がある。その時に
指数関数の底を変える
という方法を使う。たとえば$10=2^{3.321928094887362\cdots}$なので$10^3=1000,2^{10}=1024$だから$10^3\fallingdotseq2^{10}$である(コンピュータの世界で「キロ」と言ったら1000ではなく1024を指すことが多い)。ゆえに$10\fallingdotseq 2^{10\over3}$。、
\begin{equation} 10^{x}=2^{(3.321928094887362\cdots)\times x} \end{equation}となる。この${3.321928094887362\cdots}$という数字は10は2の何乗か?という疑問の答えであるが、それも一つの関数である。この関数は次の節で考える。