
微分の最も重要な応用(ニュートンはまさにこのために微分を作った)は速度の定義である。速度は時間tを独立変数にして、座標(物体の位置)xを従属変数とした微分
$$ v(t)=\lim_{{\Delta t}\to0}{{\Delta x}\over {\Delta t}} = {\mathrm dx\over \mathrm dt} $$${{\Delta x}\over {\Delta t}}$で定義される速度は${\Delta t}\neq0$でないと意味がないから、「有限の時間だけ待って、その間に進んだ距離を使って計算される量」だということになる。しかしでは例えば車のスピードメータが指している「時速60キロ(60 km/h)」は別に1時間待ってから測定するものではない具体的には車輪に連動している発電機から流れる電流などで測定されているだろう。。むしろ「瞬間の速度」というものが物理的には存在している。速度を座標と関連付けて計算する操作が微分である。
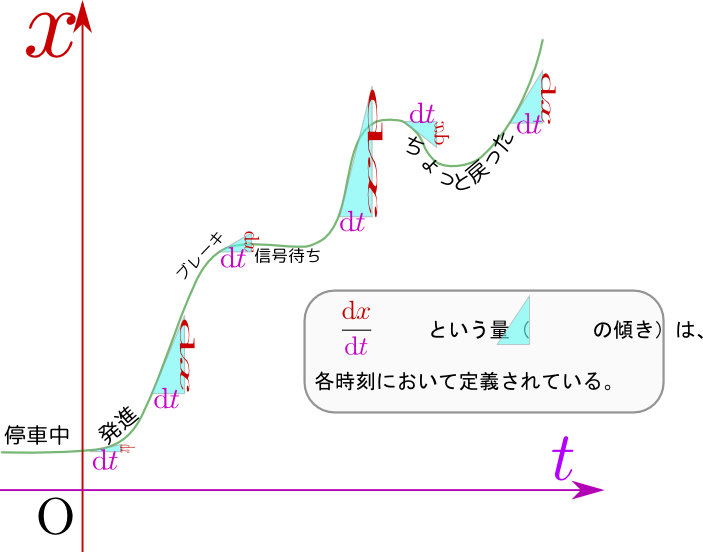
では、下のグラフで速度と微分の関係を直感しよう。