三角関数の微分（cos）

Processing math: 100%

cosの微分

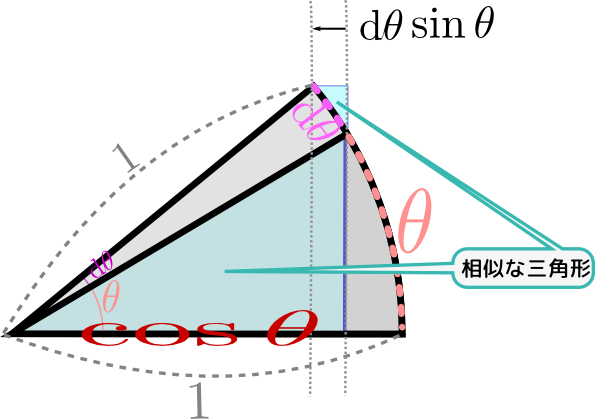
こっちはまず図で考えよう。右の図は、 $\sin$ の微分の時と同様、斜辺が1の直角三角形の角度を少し変えてみたものだが、今度は底辺である $\cos \theta$ の変化を見ている。やはり相似な三角形ができていることを考えると、 $\cos \theta$ の変化量は $\sin {\theta} \mathrm d\theta$ ということになりそうである。

ところがここで注意すべき点があって、それはこの $\cos \theta$ は減っている（変化の方向が負の方向である）ということである。ゆえに、\wrapfigen

cosの微分

$\begin{equation} \begin{array}{rl} \mathrm d (\cos {\theta})=& -\sin {\theta} \mathrm d\theta,~~~ {\mathrm d \over \mathrm d\theta}(\cos {\theta})= -\sin {\theta} \end{array} \end{equation}$

のように符号をつけるのが正しい。

ではこれも動画で実感しよう。

　cosθとその微分である-sinθを表現している動く図である。

　左の単位円の部分は、前ページのグラフに比べて、90度反時計回りに回した状況になっていることに注意。

タブレットで見ている人はむしろこの画面を時計回りに90度回してみた方がよいかも。

θ=0.7854ラジアン（45度）

sinθ=0.7071,cosθ=0.7071

↑の棒の角度はドラッグによって変えることができる。

　アニメーションのように、θが変化していったときにsinθとcosθがどのように変化していくかを考えると、それぞれの微分がどうなるかがわかる（はずである）。

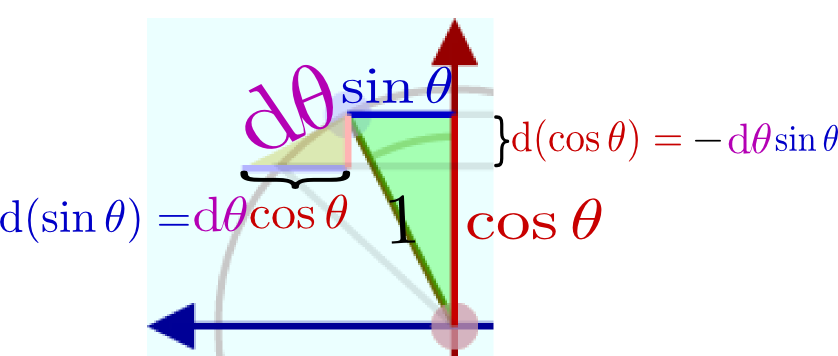
左の図が、それぞれの長さを描き込んだもの。

　右のグラフに、cosθのグラフの傾きが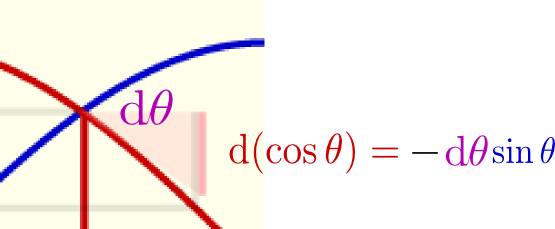のように表示されている。これも動径をドラッグすることができるので、動かしながら「cosθの微分（傾き）は-sinθだな」ということを実感して欲しい。

$\sin$ と同じ手順で数式で考えることもできる。三角関数の加法定理を使って、

$\begin{equation} \begin{array}{rll} \cos ({\theta}+\mathrm d\theta) =&\cos {\theta} \cos \mathrm d\theta - \sin {\theta} \sin \mathrm d\theta&ここで、{\cos\mathrm d\theta=1,\sin\mathrm d\theta=\mathrm d\theta}\\ =&\cos {\theta} \underbrace{- \sin {\theta}}_{微係数} \mathrm d\theta\\ \end{array} \end{equation}$

を得るから、 ${\mathrm d \over \mathrm d\theta}(\cos {\theta})= -\sin {\theta}$ となる。

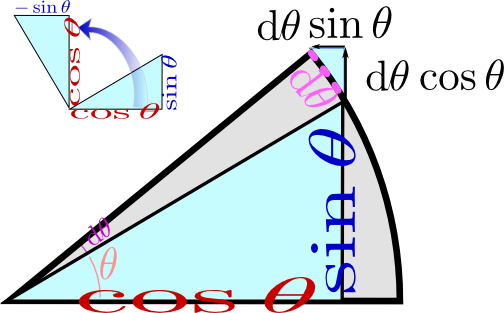
この（一方にマイナス符号がつく意味）は、左の図のように、微分という操作がちょうど「90度 $\left({\pi\over 2}\right)$ の回転に対応していると思ってもよいだろう。

${\pi\over 2}$ の回転はのように、 $x$ 座標を $y$ 座標に、 $y$ 座標を（符号を変えて） $x$ 座標にすることで得られる。式で書くなら $(x,y)\to(-y,x)$ であるが、これが微分 $(\cos \theta,\sin \theta)\to(-\sin \theta,\cos \theta)$ と同じ計算になっているわけであるθが増加するという現象を原点を中心とした円運動と捉えると、微分というのは速度を計算することだから、円運動の速度は動径と垂直だ、ということを示していることになる。。

なお、 $\cos^2{\theta}+\sin^2{\theta}=1$ を微分するという方法でも ${\mathrm d\over \mathrm d\theta}\cos{\theta}$ を計算できる。

$\begin{equation} \begin{array}{rl} 2\cos{\theta}{\mathrm d (\cos{\theta})} + 2\sin{\theta}{\mathrm d (\sin{\theta})} &=0 \\ {2\cos{\theta}}{\mathrm d (\cos{\theta})} + {2}\sin{\theta}{\cos{\theta}}\mathrm d\theta &=0 \\ {\mathrm d (\cos{\theta})} =&- \sin{\theta}\mathrm d\theta \end{array} \end{equation}$

この出し方を見ると、 $\sin{\theta}$ と $\cos{\theta}$ の微分のどちらかにはマイナス符号が必要だったことがわかる。

←sinの微分のページに戻る　tanの微分のページへ→