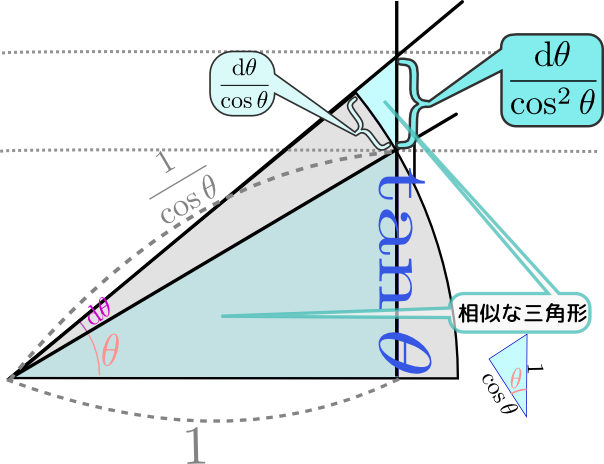
まず、図解で示そう。

上の図のように、底辺1で底辺と斜辺のなす角が${\theta}$である直角三角形を描く(この直角三角形の高さが$\tan{\theta}$である)。角度が\mathrm d\theta だけ大きくなった時、この直角三角形の高さがどれだけ高くなるか、を考えれば$\tan {\theta}$の微分がわかる。
この直角三角形の斜辺の長さは${1\over \cos{\theta}}$であるこれを求めるのに、「公式$1+\tan^2{\theta}={1\over \cos^2{\theta}}$を使って…」などとやり始める人がたまにいるのだが、そんな面倒なことは全く必要ない。${底辺\over 斜辺}=\cos {\theta}$という式を思い出せばすぐに出る。から、図に書いた円弧の部分の長さは${\mathrm d\theta\over \cos{\theta}}$である。また相似な三角形ができているから、その相似の関係を使えば、高さの増加は${\mathrm d\theta\over \cos^2{\theta}}$とわかり、結果として${\mathrm d \over \mathrm d\theta}\tan{\theta}={1\over \cos^2{\theta}}$が導かれる。
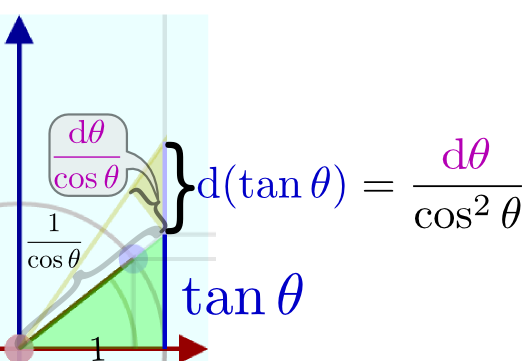
アニメーションのように、θが変化していったときに縦軸の座標tanθがどのように変化していくかを考えると、微分がどうなるかがわかる。
左の図は上のグラフに長さを描き込んだものである。この場合、底辺が1なので、高さが(1/cosθ)であることに注意しよう。
動径の棒をドラッグして動かすことができるので、いろんな場合について確かにtanθの変化(増減)が(1/cos2θ)に比例していることを動かしながら実感して欲しい。
${y}=\tan{\theta}$の微分を数式を用いて行うには、$\tan {\theta}={{\sin {\theta}\over \cos{\theta}}}$としてから、以下のように行う(もちろん分数関数の微分の式に代入して考えていってもよい)。
\begin{equation} \begin{array}{crll} &\cos{\theta}\times{y} =&\sin {\theta}&ここで両辺を微分\\ -\sin{\theta} \mathrm d\theta\times{y} +&\cos{\theta}\times \mathrm dy =&\cos {\theta} \mathrm d\theta &ここで、\cos {\theta}で割る \\ - \underbrace{\sin{\theta} \over \cos{\theta}}_{\tan{\theta}} \mathrm d\theta\times\overbrace{\tan{\theta}}^{{y} }& +\mathrm dy =&\mathrm d\theta \\ &\mathrm dy =&\underbrace{(1+\tan^2 {\theta})}_{{1\over \cos^2{\theta}}}\mathrm d\theta = {1\over \cos^2{\theta}}\mathrm d\theta \\ \end{array} \end{equation}