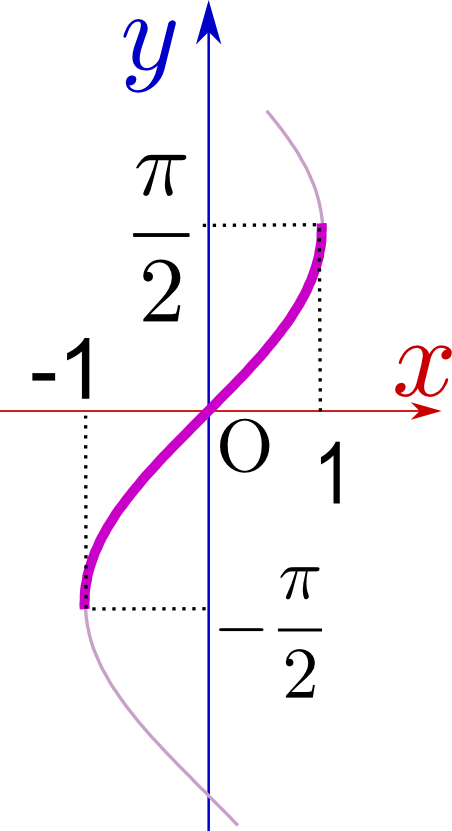
この三つは$\sin,\cos,\tan$の逆関数だから、逆関数の微分の式を使ってもよいし、たとえば${y}=\arcsin{x}$を微分するなら、まず${x}=\sin{{y}}$とした後、
\begin{equation} \begin{array}{rl} {x}=&\sin{y} \\ \mathrm dx=&\cos{y}\mathrm dy\\ {\mathrm dx\over \mathrm dy}=&\cos {y}=\pm\sqrt{1-{x}^2}\\ {\mathrm dy\over \mathrm dx}=&\pm{1\over \sqrt{1-{x}^2}}\\ \end{array} \end{equation}のように微分を行う。ここで複号$\pm$をどうするかが問題となるが、グラフを見るとわかるように、$\arcsin$はこの定義域・値域の中では常に増加する関数であるから、${\mathrm d\over \mathrm dx}\arcsin{x}={1\over \sqrt{1-{x}^2}}$とする値域を変えると、増加する関数とは限らないから、その場合は符号を調整する必要がある。。
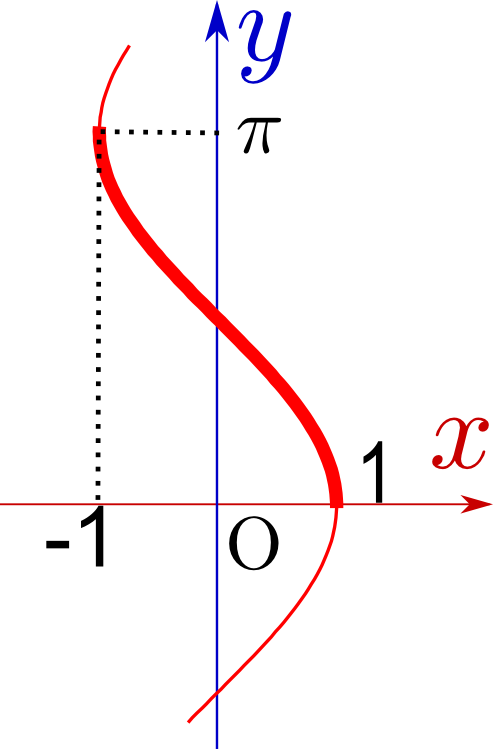
$\arccos$の微分も同様に、
\begin{equation} \begin{array}{rl} {x}=&\cos{y} \\ \mathrm dx=&-\sin{y}\mathrm dy\\ {\mathrm dx\over \mathrm dy}=&-\sin {y}=\pm\sqrt{1-{x}^2}\\ {\mathrm dy\over \mathrm dx}=&\pm{1\over \sqrt{1-{x}^2}}\\ \end{array} \end{equation}となるが、今度はグラフからわかるように減少関数(右下がり)なので、${\mathrm d \over \mathrm dx}\arccos {x}=-{1\over \sqrt{1-{x}^2}}$となる。
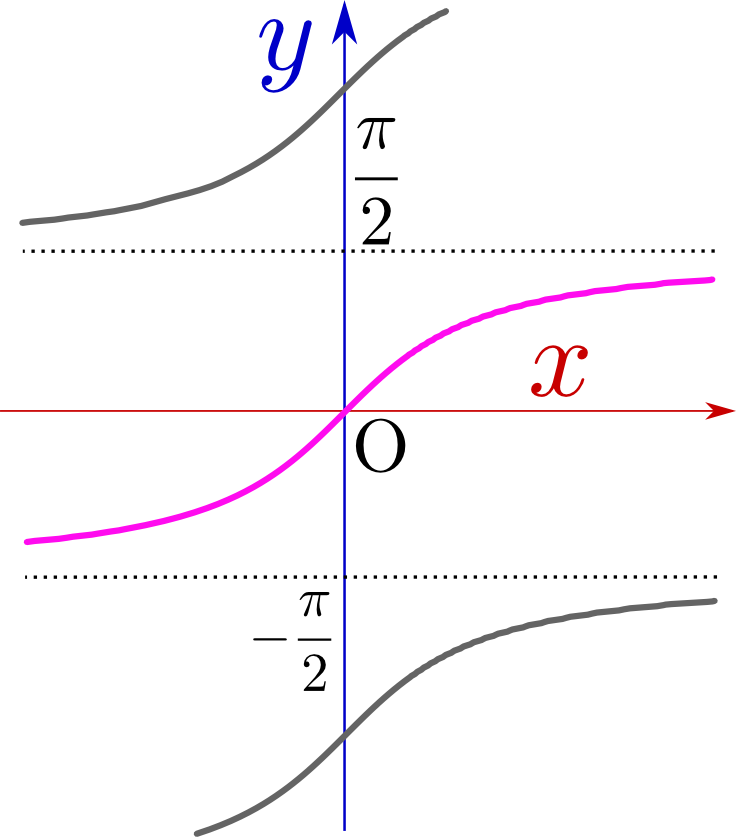
最後に$\arctan$の微分は${x}=\tan{y}$から${\mathrm dx\over \mathrm dy}={1\over \cos^2{y}}=1+\tan ^2{{y}}$として、
\begin{equation} \begin{array}{rl} {\mathrm dx\over \mathrm dy}=&1+\tan^2{y}=1+{x}^2\\ {\mathrm dy\over \mathrm dx}=&{1\over 1+{x}^2}\\ \end{array} \end{equation}となるので、${\mathrm d \over \mathrm dx}\arctan{x}={1\over 1+{x}^2}$となる。$\arctan$という「ややこしそうな関数」の割に、微分の結果が単純な${1\over 1+{x}^2}$になるというのは面白いところである。
以上をまとめておく。