自然科学のための数学2015年度第18講
まず、第16講でもやった「微分方程式を図解する」の最後のページで、いろんな微分方程式とその解の図を動かしながら遊んでもらった。
ここで、
- 微分方程式は「傾き」を決める方程式であること。
- 「微分方程式を解く」とは、「傾きから『どのような線が引けるか』すなわち関数の形を決める」という作業だあること。
- したがって微分方程式の「解」は1本の曲線ではなく、曲線の集まりになること
を実感してもらったところで、微分方程式の解の含むパラメータについての話に入った。
微分方程式の解に含まれるパラメータの数
微分方程式の解には微分方程式だけでは決まらないパラメータが必ず含まれる。それは微分方程式が局所的情報を表す式であることからくる必然的性質である。微分方程式を解く時にもこの点は大事なので、そのパラメータの数について考察しておこう。${\mathrm dy\over \mathrm dx}={y}$の解が${y}=A\mathrm e^{{x}}$だったことを例として考えよう。
パラメータ$A$は変数分離を行った結果の${\mathrm dy\over {y}}=\mathrm dx$を積分するときの積分定数から現れる。具体的な積分結果は$\log{y}={x}+C$であるが、$ {y}=\mathrm e^{{x}+C}=\mathrm e^C \mathrm e^{{x}}$となるから、$A=\mathrm e^C$である。
次に二階微分方程式の簡単な例$\left({\mathrm d\over\mathrm dx}\right)^2f({x})={\mathrm d\over\mathrm dx} f({x})$を同様に解いてみよう。
\begin{equation} \begin{array}{rll} \left({\mathrm d\over\mathrm dx}\right)^2f({x})=&{\mathrm d\over\mathrm dx} f({x}) &{両辺を不定積分} \\[-2mm] {\mathrm d\over\mathrm dx} f({x})=&f({x})+C \end{array} \end{equation}と、ここまでできたところで、この後どうする?と聞いてみた。
こういうときは、まだわからない$f(x)$と、未定の$C$を「わからないものどうし」でまとめてしまうという手がある。すなわち、${y}=f({x})+C$と置く。
すると、 \begin{equation} \begin{array}{rll} {\mathrm d\over\mathrm dx} (y-C)=& y&{{\mathrm d\over\mathrm dx}(-C)=0を使って、さらに変数分離}\\[-2mm] {\mathrm dy\over {y}}=& \mathrm dx&{もう一度積分}\\[-2mm] \log {y}=& {x}+D&{\mathrm e の肩に乗せて}\\[-2mm] {y}=&\mathrm e^{{x}+D} \end{array} \end{equation}
こうして解は($f({x})$に戻して)$f({x})=-C + \mathrm e^{{x}+D}$または$f({x})=-C+D'\mathrm e^{{x}}$($D'=\mathrm e^D$)となり、積分を二度やった結果として積分定数$C,D$(または$C,D'$)の二つのパラメータが現れる。
微分方程式を解くとは積分すること、と考えると「$n$階微分方程式なら不定積分を$n$回繰り返せば解ける」と言えて、結果は$n$個の積分変数を含む。上の具体例を見ると、確かに一階微分方程式の解は1個の、二階微分方程式の解は2個の積分定数を含んでいる。
結論として、$n$階微分方程式の解は常に$n$個の「微分方程式だけでは決まらないパラメータ」を含んでいるただし、途中で関数が定義できない点(たとえば${y}={1\over {x}}$の${x}=0$)があると積分一つに対して二個の積分定数が出て来ることもあるので、そのような場合には注意が必要である。。
一階微分方程式で正規形の場合で、「決まらないパラメータ」の意味を考えておこう。
${\mathrm dy\over \mathrm dx}=f({x},{y})$は、${x}$-${y}$平面上である点$({x},{y})$を指定したとき、その点における関数のグラフの傾き${\mathrm dy\over \mathrm dx}$、すなわち各点各点において「グラフの線はどちらに伸ばすべきか」を与える式である。
最初に考えた微分方程式${\mathrm dy\over \mathrm dx}={y}$の解の曲線は、各場所において${y}$座標と同じ傾きを持つ。解の曲線を次々と描いていくと、次のグラフにあるように全平面を埋め尽くす。
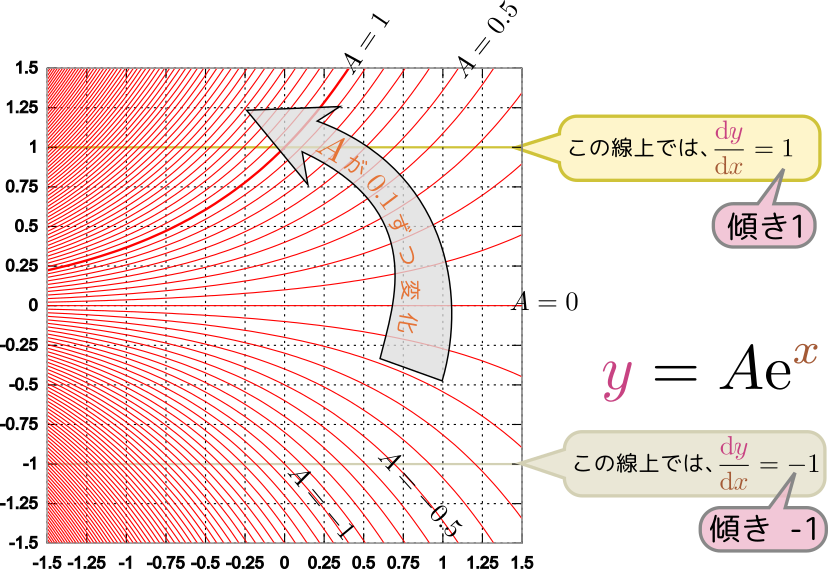
${x}=0$の時${y}=1$というふうに「出発点」を決めると、この場合は${y}=\mathrm e^{{x}}$という線(グラフでは1本だけ太い線で表現した)の上を進んでいく。
一階微分方程式が指定するのは傾きのみであるから、出発点(上の例では${x}=0$から始めたが、実はどの場所でもよい)を指定すれば曲線は一つ決まる。別の点を出発点にすれば(たまたま同じ線上の2点を選ばない限り)また別の線が引ける。たとえば${x}=0$の時${y}=2$と決めたなら、${y}=2\mathrm e^{{x}}$の上を進む。こうして、微分方程式だけからは決まらないパラメータが解には入っている(後で、それを「初期条件」などで決めていく方法について述べる)。