ここでは、Smolinの"The fate of black hole singularities and the parameters of the standard models of particle physics and cosmology"の紹介をする。この論文およびそれに関する一連の論文についての説明は、Rüdiger Vaasの"Is there a Darwinian Evolution of the Cosmos?"というページにあるので、そっちを読んでもいいかもしれない。
まず、我々の知る宇宙の中では、１秒に100個ぐらいブラックホールが生まれているらしい。この数字は銀河の数10^12個に、40年に一回ぐらいTypeIIの超新星が生まれるということを考え、そのうち1/10から1/100がブラックホールを作るだろう、という計算から出たらしい。つまり我々の宇宙でブラックホールが生まれる率は実は結構高い、ということである。まずこれ注意その１ね。
さて、物理学上の難問の一つとして、なぜ我々の宇宙の住む物理定数がこういう値になっているのか、という問題がある。これには
のようないろいろな答えがある。さてそこで、上で述べたブラックホールの生成率に関係しそうな物理定数をあげてみよう。Smolinによれば、主系列星が存在するためには、以下のようなパラメータに制限がつけられるという。
１は陽子の安定性に、２、３は原子のサイズに関係する。４、５は核反応に関与する、ということだろう。さらにTypeII型の超新星が存在するためには、弱い相互作用の結合定数と万有引力定数の間にもある関係がなくてはならない。つまり、我々の宇宙はこれらの物理定数が、ブラックホールを生成させるのにちょうどいい値になっている、ということである。これが注意その２ね。
さて、我々の宇宙がブラックホールを生成させるのにちょうどよい物理定数を持っているのは偶然か？
偶然ではない、というのがSmolinの立場である。この考えを説明するためには、星が重力崩壊する時にブラックホールの内側では何が起こるのか、という話をしなくてはいけない。
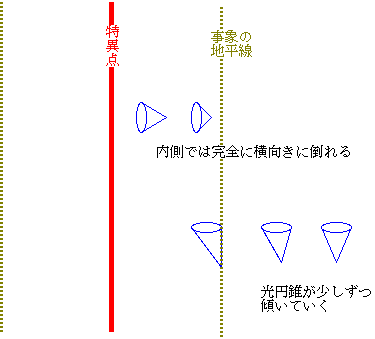ここでブラックホールの内側の特異点ってどのようになっているか、という話をちゃんと書いておこう。ブラックホールの内側の時間というのは、非常にわかりにくい流れ方をしている。左の図はブラックホールの時空図というやつで、縦軸が時間、横軸が空間（半径方向）である。図で青で書き込んでいる円錐はいわゆる光円錐であり、一点（円錐の頂点）から出た光が時間がたつと広がっていく様子を表している。ブラックホール付近では光はブラックホールに向かって“落ちる”ので、図の下の方に書いてあるように、光円錐はブラックホールの中心に近づくような方向に傾く。普通の場合（図で右端とか）では光円錐はどちらにも広がる（つまり、外に出る光も内に向かう光もある）のだが、事象の地平線のところで、外に出る光がなくなる。
さらに内側に入るとどうなるかというと、なんと、光円錐が完全に横倒しになってしまう。「事象の地平線を越えてしまうと中に入ることしかできなくなる」とよく本に書いてあるが、それは我々が未来にしか進めないのと同じことである。別の言い方をすれば、「ブラックホールの内側では中心方向に向かって時間が流れている」ということになる。
余談であるが、ホワイトホールというのは、この内側光円錐が逆向きに倒れている（外にしか進めなくなっている）ものを言う。事象の地平線の外側についてはブラックホールと同じである。「ブラックホールは引力だから、ホワイトホールは斥力だろう」なんて思うと大間違いなので注意。
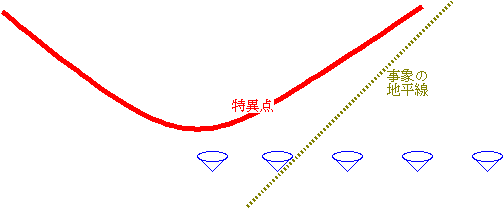さて話をもどして、「中心方向に時間が流れるなんてめんどくさい。時間はちゃんと時間方向に流せっ」と怒る向きもあるだろう。そういう人のために、時間がちゃんと図の上に向かって流れるように書き直したのが右の図である。事象の地平線は、上の図でわかるように本来、その上を光が走るような線である。そこで時間がちゃんと上に流れるように図を書くとすれば、事象の地平線は傾いた線になってしまう。そして、上の図では縦線だった特異点（ブラックホールの中心）は“未来側”にあるので、図のように天井のように上からふたをしたような形に変わってしまう。
つまり、ブラックホールの特異点というのはブラックホールの真ん中にあるというよりは、ブラックホールの“未来”にあるのである。
っていってもなんかわかりにくいだろうけど、よく「ブラックホールは入ったら出てこれない」と言われるが、それは「未来から過去にはいけないじゃん」ということと同じ理由なんだな、という感じでなっとくしてくれるといいかも。
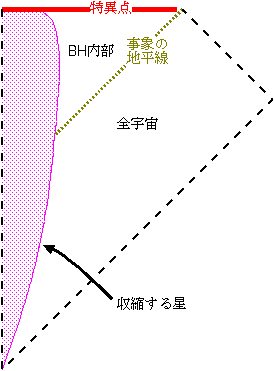
さて、上の図をさらに適当にのばしたり縮めたりして、宇宙が四角形になるようになおしたものをペンローズダイアグラムと言う。具体的には左の図のように書く。左の図には、収縮してブラックホールになっていく星の物質がどんなふうに縮んでいくのかを表す図も書いておいた。
この書き方だと特異点（といいながら線なんだけど）が水平になる。紫色で書いた「収縮する星」を表す物質が特異点に向かって落ち込んでいくという図である。
なんせ適当に伸び縮みさせているので、ＢＨ内部が全宇宙の半分くらいの面積があるように書かれているけど、これは図の書き方のトリックであると理解してほしい。この図を、「光は右上または左上４５度に進むのだ！」という点に注意しながら見ると、
「おおお、えらいこっちゃ、事象の地平線を越えたら元の宇宙に帰ってこれんではないかああああ」
ということが実感できるはずだ。できない人はこの図にあきるまで４５度の傾きの線を書いてみること。
さて、ブラックホールが形成される時、大量の物質が中心に向かって落ちていく。そして、古典力学的に考えるならば、ある一点（シュワルツシュルト型の場合）に全ての物質が落ち込み、密度∞の特異点（図の赤線）がそこにできる、ということになる。質量密度が∞になってしまう。で、「困った困った」ということになるのだが、どうせここは事象の地平線の向こう側で目に見えないんだし気にしなくていいや、という考え方もある。
一方、宇宙の始まりもこういう質量密度∞の状態だった、って話があって、そっちもなんとかしなくちゃいけないという話がある。こっちは事象の地平線の中に隠れているわけではないので、その分問題は深刻である。この問題に対する解決として、量子論を使って特異点を回避しようというのが、ホーキングの「無からの宇宙生成」というやつで、無からトンネル効果で突然宇宙が生まれる、という話にして宇宙の始まりにあるはずの特異点を回避しようとしている。
ブラックホールの特異点についても量子力学を適用するならば、そんなふうに密度∞の場所はできないのではないか、という話がある。量子重力が必要になるような密度（プランク密度とSmolinは呼んでいる。プランク長さの立方体の中にプランク質量が入っているぐらいの密度だろう）になると、量子効果によってbounce（反発）が起こり、また領域が広がりはじめるはずだ、というのである。このあたりの話は、この論文には詳しくは書いてない。実際のところ、物が量子重力となると、現代の物理では何も確かなことは言えないんで、「量子重力が必要なぐらいごっつい密度になれば、そんなこともあるやもしれんなあ」というぐらいでおおらかに聞いてくれるとありがたい(^^;)。
さて、ではこの量子効果によって膨張し始めた領域はどうなるだろうか。膨張してブラックホールの外に出るかというと、それはできない。特異点ができはじめるという時はもう事象の地平線の形成は終わっているので、今さら量子効果で膨張しても、ブラックホールの外には出られない。となると、せまいはずのブラックホールの内側に広い広い空間ができあがる、ということになる。つまり、ブラックホールがある宇宙は、子供宇宙を生みだせるのである。これ、注意その３ね。Smolinたちはこれは新しいビッグバンであって、こうやってできた、ブラックホールの中の広い広い空間こそ、もう一つの宇宙だと考えているのである。
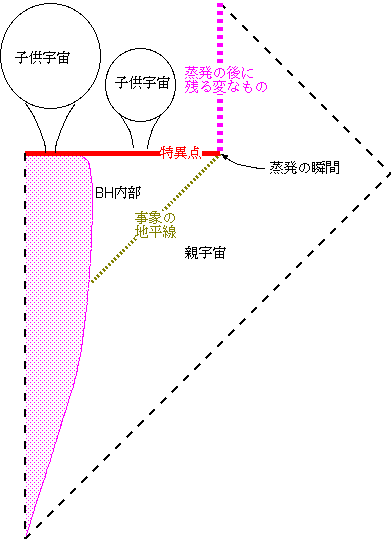ブラックホールの内側で子供宇宙ができる様子を書いたのが左の図である。事象の地平線の内側にできた特異点（赤線）でエネルギー密度が∞になる…寸前で量子効果によりぼこぼこと宇宙が発生するわけだ。この宇宙の発生も同様に事象の地平線の中なので親宇宙にいる人間には観測できない。
この事情はたとえブラックホールが蒸発したとしても同じである。左の図はブラックホールが後で蒸発する場合で書いてある。実際、蒸発の瞬間と宇宙の誕生は、この図では“同時”に起こっている。もともと相対論をやっている以上、“同時”なんてたいした意味はないのだが、とにかくブラックホールが蒸発する場合でも、蒸発する前に（この図だと同時だが）子供宇宙を生み出すことはできるわけである。
ところで「蒸発の後に残る変なもの」って何だ、と聞きたくなる人はたくさんいるだろうけど、いまんところ「変なもの」としかわかってない、文字通り変なものなので聞かないでほしい。
ここで一つ、大きな仮説を置く。この仮説を最初にいいだしたのはWheelerらしい。その仮説とは「新しい宇宙での物理定数は、ブラックホールがあった宇宙の物理定数と、ちょっとだけ、ランダムに変化したものになる」というものだ。Smolinは、こう考えてもこれまでの統一理論などには反しないはずだ、と言う。たとえば大統一理論では、もともとの対称性がいろんな形に破れていく過程で今の物理定数（陽子の質量とか電子の質量とか）が決まると言っているのだから、ブラックホールの内側でいったんプランク密度まで圧縮してから「はい御破算でやり直し」と宇宙を再出発させれば、物理定数が変わることだって十分ある、と言いたいわけだ。
つまり、ブラックホールから生まれた子供宇宙は、元の宇宙と似ているがちょっと違うのである。これ、注意その４ね。
と、ここまで来ると、この注意その１からその４までから、どういう結論が導き出されるのか、賢明なるＳＦファン諸氏には想像がつくはずだ。
子供宇宙は親宇宙とは少し違った物理定数を持った宇宙になる。もしその子供宇宙の物理定数が変化しすぎていて、恒星が全くできなかったら（たとえば核力が弱くなり過ぎたら核融合なんておきなくなるかも）どうなるだろう。あるいは恒星ができてもブラックホールができなかったら？（ほんのちょっと物理定数が違えば中性子の縮退圧がものすごく強くなり、中性子性になった段階でそれ以上に重力崩壊が起きなかったら、ブラックホールになってくれない）
そういう宇宙は、子供宇宙を持てない。逆に恒星がたくさんでき、その中のでっかい星がどんどんブラックホールになるような宇宙は、そのブラックホールの中でまた子供宇宙がたくさんできる。
つまり、ブラックホールを作る能力を持った宇宙は、どんどんその数を増やしていくのである。
我々の宇宙でブラックホールがたくさん生まれているのは偶然ではない。そういう性質を持った宇宙だからこそ、存在が許されているのである。
最初の宇宙（アダム？）ができてから何世代の宇宙が経過しているのかはわからないが、新しい宇宙の発生が常にこのメカニズムによるのなら、何世代か後にはブラックホールを作れる宇宙しか残りませんよ、と言われても「そりゃそうか」という気になる。ならない？ なるでしょ？ なるよねー。
この話は生物のダーウィン的進化と同じだよ、とSmolinたちは言っている。生物の繁殖に対応するのがブラックホールによる子供宇宙発生であり、遺伝子に対応するのが物理定数である。突然変異に対応するのが、ブラックホールの中で宇宙が生まれる時の物理定数の変化である。物理定数の変化自体はランダムなのだが、その結果ブラックホールを作れない宇宙ができると、その宇宙は淘汰される。そして、たくさんの子孫を残せる生物がたくさん子孫を残すがゆえに繁栄するように、たくさんのブラックホールを作れる宇宙はたくさんブラックホールが作れるがゆえにたくさん存在するのである。
そんなうそみたいな話がうまくいくんかぁ？？というのがここまで読んだ人の素直な反応だと思う。実際、Rüdiger Vaasの"Is there a Darwinian Evolution of the Cosmos?"というページでも、いろいろ問題点があげられている（と同時にうまくいきそうな話もあげてある）。
smolinがあげている根拠を紹介しておこう。
ということである。
７つの条件その１をあげると、Δｍ＝（中性子の質量）−（陽子の質量）が１８MeVより大きいと、炭素より大きな原子核は安定に存在できない（中性子がベータ崩壊する確率が高くなってしまうからだろう）。核力が弱すぎたり、弱い相互作用が強すぎたりしても同様のことがおこる。
安定性より強い条件としてあげられる条件その２は、恒星の中での原子核の合成が起こるかどうかという問題。Δｍが現在の値の２倍になってしまうと、重陽子すら存在できない。強い相互作用の結合定数が３１％増えると重陽子はできない。一方、１３％減ると陽子二個（ヘリウム２？）や中性子二個の原子核（原子番号０？）ができてしまう。このような原子核の安定性および生成される量は、星の進化に重大な影響をもたらす。たとえば星の内部では核融合により合成された炭素は星の形成に影響を与えている。星間分子雲が集合して星になる時、一酸化炭素が分子雲を冷やして集合させるのに重要な役割をしているのである（とりあえず、星間分子雲に一酸化炭素が豊富にあるのはほんとう。一酸化炭素がどう星間分子雲を冷やすのかは、私はよく知らない）。よって、炭素のような原子核が安定して存在できる状況にないと、星ができる可能性が減る。当然ブラックホールも減る。そんな宇宙は子孫（子孫宇宙ですが）を残せない。
ここでさらにつっこんだ話を書いておくと、SmolinやVaasは、炭素が存在することが星、ひいてはブラックホールの形成に関係するということは、「我々炭素系の生命がこの宇宙にいるのは、宇宙が炭素を生むように（そしてブラックホールを造るように）進化したからである」という、人間原理の新バージョンみたいなことを考えているようだ。この場合、人間は宇宙がブラックホールを作ろうとした結果できた、一種の副産物に過ぎない。そういう意味では人間原理とは言い難い。「利己的なブラックホール原理」ってとこでしょうか。Vaas自身「原理的にはブラックホールの数と生命は関係ないんだけどさ」と副産物的な話であることを認めている。
この辺いじればＳＦのネタになんぼでもなりそうですな。
とかさ。
条件その３は、恒星内の水素の安定性と光圧が恒星をささえること。詳細は書いてないが、これで陽子と電子の質量に制限がつく。条件その４は、convective starの存在なんだそうだけど、これって何だっけ？ これも陽子と電子の質量に関係します。
条件その５は超新星が存在するためにはニュートリノがちょうどいいだけエネルギーを持ってでなくちゃいかんから、というわけでニュートリノの相互作用に制限がつくって言うんだけど、超新星じゃなくじわーっと冷えてブラックホールになるというのは（もちろん我々の世界ではないけど）ありじゃないんかな。そのあたりちゃんと計算しているんだろうとは思うけど、ようわからん。
条件その６は、陽子の寿命が十分長いこと。大統一のエネルギースケールに影響を与えます。
条件その７は、主系列星の存在条件なんですが、これがパラメータにシビアだというのは、人間原理の話でよく出てくる話。黒体輻射が一様等方だから、宇宙のはじめにはブラックホールはなかったはずだ、ということは後で主系列星の崩壊でできた、というふうに話を持っていくんですが、宇宙のはじめにブラックホールがある方が「早熟な宇宙」ということで有利、という話にはならんのでしょうか。気になるところであります。
えー、似たような話がいろいろあります、という話がまだ続くんですが、とりあえずこんだけ。