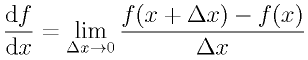
はじめに高校・大学で「微分」というものを勉強している人の中には「これいったいなんだろう?」「いったい何のためにこれがいるのだろう?」と疑問に思いつつ、ただ「sinを微分したらcos、cosを微分したら-sin」のように機械的に憶えている人もいるようである。ここでは、動く図形を使って微分という計算がどういう意味を持っているのか、を説明してみようと思う。 |
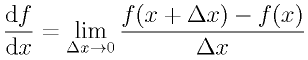
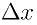 のΔは「変化量」を意味する記号で、「
のΔは「変化量」を意味する記号で、「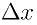 」で一つの量であって、Δ×
」で一つの量であって、Δ×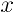 の意味ではないので注意。
の意味ではないので注意。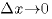 の極限というところがなかなか難しい。そこで、
の極限というところがなかなか難しい。そこで、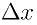 を変化させることでどのように関数が変化していくかを、図で表現すると(この図の▲と▲はマウスでつかんで動かせます!!!)
を変化させることでどのように関数が変化していくかを、図で表現すると(この図の▲と▲はマウスでつかんで動かせます!!!)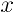 であり、▲で示した場所が位置
であり、▲で示した場所が位置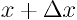 である。二つの間の距離が
である。二つの間の距離が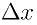 である。図に示した緑の三角形の底辺が
である。図に示した緑の三角形の底辺が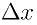 であり、三角形の高さが
であり、三角形の高さが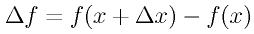 である。微分の極限を取る前の量
である。微分の極限を取る前の量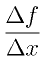 は、この三角形の斜辺の傾きを表現している。
は、この三角形の斜辺の傾きを表現している。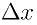 を0に近づけることにより、三角形の斜辺はどんどんこの青い線に近づく(完全に重なった時は水色で表現している)。
を0に近づけることにより、三角形の斜辺はどんどんこの青い線に近づく(完全に重なった時は水色で表現している)。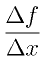 になる)。
になる)。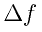 と
と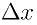 がどのようになるかを実感して欲しい。この二つを近づけていくと、
がどのようになるかを実感して欲しい。この二つを近づけていくと、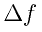 と
と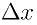 がともに0に近づく。こうして0に近づいていった時の
がともに0に近づく。こうして0に近づいていった時の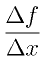 の極限(底辺を1にした時の三角形の高さ)こそが微分である。
の極限(底辺を1にした時の三角形の高さ)こそが微分である。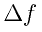 と
と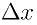 がいっせいに0に近づいていく時に、その比が一定値に近づいていく。この一定値が微分
がいっせいに0に近づいていく時に、その比が一定値に近づいていく。この一定値が微分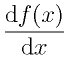 という量である。
という量である。| ここで▲と▲をいろいろな場所に動かして、三角形の斜辺の傾きがどうなるか、を動かしてみることで確認して欲しい。 こうやって「 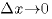 極限での傾き」を決めていくのが、微分という計算である。 極限での傾き」を決めていくのが、微分という計算である。 |
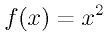 のグラフであり、つまりfは一辺
のグラフであり、つまりfは一辺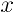 の正方形の面積である。そこで、正方形を図に書き込んだものを用意した。
の正方形の面積である。そこで、正方形を図に書き込んだものを用意した。