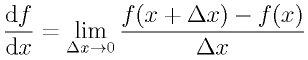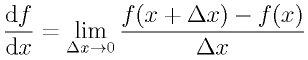微分ってなあに？（その１）
微分の雰囲気を知るために、まずは下のグラフで「遊んで」みましょう。
二つの▲は（マウスまたは指で）つかんで動かすことができます。ちなみにこのグラフはy=x2のグラフです。
微分の定義を確認しましょう。ある関数f(x)の微分とは、
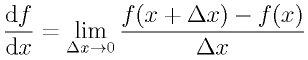
です。Δは「変化量」を意味する記号で、「Δx」で一つの量であって、「Δとxの掛け算」の意味ではないので注意しましょう。
分子にあるf(x+Δx)-f(x)を、グラフの中では「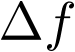
」と書いています（これはもちろん、「ｆの変化」という意味です）。
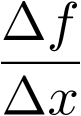はグラフに現れる三角形の傾きです。グラフの右横に、その三角形と相似で底辺が「１」である三角形を表示してありますが、この三角形の高さが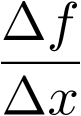です。
この式に現れる極限（lim）というところがなかなか難しいところなのですが、上のグラフで二つの▲の位置を動かした時、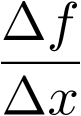がどのように変化するかを見てください。
Δx→0の極限とは二つの▲が重なるところだと考えてくれればいいです。
こころゆくまで動かして「微分を計算する」ことのイメージをつかんでください。
ある程度つかめたら、関数をかえてやってみましょう。