半減期ってなあに？（動く図を使ってHTML5版）

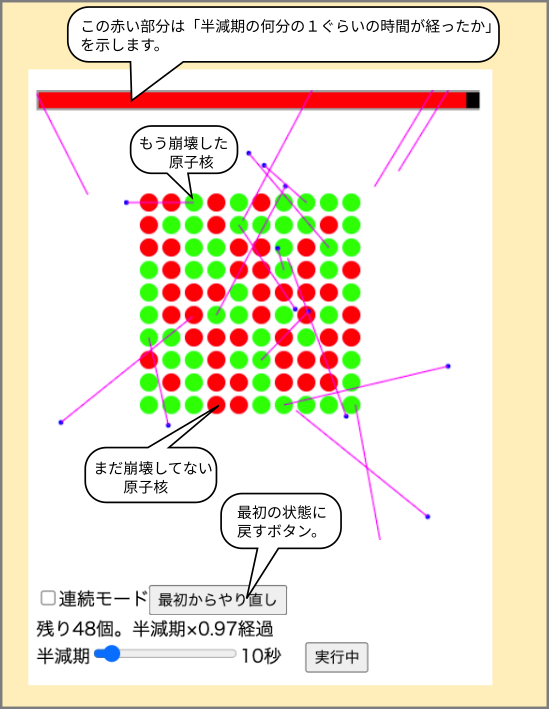
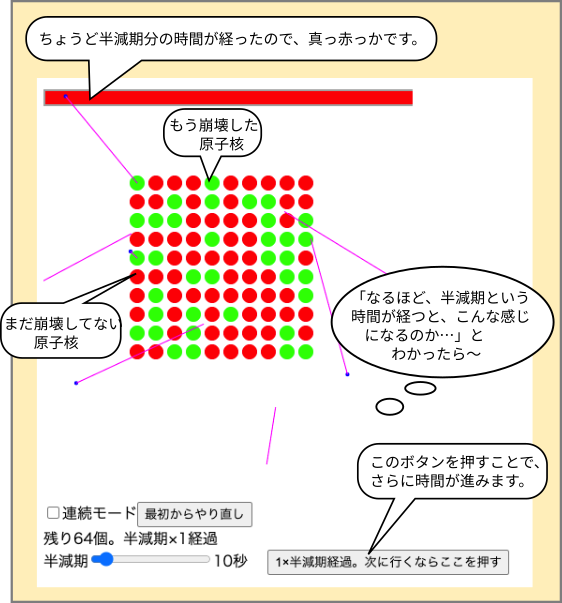
原発事故の報道の中で「半減期」という言葉がよく聞かれるようになりました。

言葉で説明されても「結局何なの？」という感想を持つ人も多いようです。こういう時こそ、動く図を使って説明してみるのもいいだろう、と思ってちょっと作ってみました。

　「半減期」は放射性物質が「崩壊」をして、元の半分の量になるまでの時間です。

と言われてもなかなか意味がわかりにくい、という人が多いと思うので、まずは↓のプログラムを見てください。

連続モード
残り100個。半減期×0経過
半減期10秒　

プログラムの使い方

　「このボタンを押してスタート」と書いてあるボタンを押すと、放射性物質赤い●が崩壊を始めます。「崩壊」は文字通り壊れることで、崩壊すると別の原子、ここでは緑の●に変わり、青い小さな●を出します。この青い小さな●がいわゆる「放射線」です。

（注意！！：こっから下のは単なる画像なので、マウスでボタン押しても、なんにも起こりません！！）

　一番上の横棒（バー）が真っ赤になったら、「半減期」という分だけの時間がたったということになります（初期設定では10秒にしてあります）。

　ここで、このプログラムの時間は一旦止まります。

　これで「なるほど、半減期という時間が経つとこうなるのか」ということを理解していただければと思います。

　この後どうなるのか、を知りたい人はどんどん一番下の「次に行くならここを押す」を押してください。さらに半減期ずつ時間が進みます。

　最初100個から始まりますが、だいたい半分ずつになっていきます。

　最初の半減期（例えば10秒）で放射性物質●は半分になりますが、次の半減期（さらに10秒。あわせて20秒）経つと、４分の１になります。

１００％　　→（半減期分の時間）→　　50％　　　→（半減期分の時間）→　　25％　　　→（半減期分の時間）→　　12.5%　　　 →（半減期分の時間）→　　7.25％　（以下同様）

となるのが正解なのです。「半分になるのが半減期なら、半減期×２でなくなるんじゃないの？」と疑問に思った人は、下のFAQその１を見てください。

　
　ここで、出てくる放射線も激しさもどんどん弱くなっていくことに注目！です。

　放射性物質によっては、崩壊してもまた別の放射性物質になり、それがまた崩壊する、という段階を踏む場合もあります。ここでは説明しやすいように単純なケースを考えています。

半減期を変えてみましょう

　さて、プログラムの最初の状態では半減期は10秒でした。ちなみに、原発事故で出てきたと言われている放射性物質の半減期は

核種	半減期
ヨウ素131	8日
テルル132	3.2日
ストロンチウム90	28.8年
セシウム１３７	30年

のようになってます。放射性物質の種類により、いろんな長さがあります。

　下の左側にあるつまみをマウスでつかんで動かすことで、半減期を１秒から600秒（10分）までの範囲で変えることができます。半減期を変えて動かしてみて、

半減期が短い→放射性物質は早くなくなる（良いこと）→その分、最初に出てくる放射線が激しい（悪いこと）

半減期が長い→放射性物質がなかなかなくならない（悪いこと）→その分、出てくる放射線は激しくない（良いこと）

を確認しましょう。
　なお、いちいちボタン押すの面倒だ、という人は、下の左側にある「連続モード」のところにチェックを入れて最初からやりなおしてください。今度は止まらずに崩壊が続きます（いつまでも）。

下に、簡単な計算機をつけておきます。

　当然ながら、「どれくらいの量の放射性物質があるのか」によって危険度は変わるし、出る放射線が人間に当たった時の被害の様子も放射性物質によって違います。半減期だけで単純な比較はできません。

このプログラムを見ながら感じ取っていただきたいこと

　まず、半減期が過ぎるごとに放射性物質の量は減っていく、ということです。だから半減期が短いということは激しい放射線を出すということでもありますが、すぐになくなってくれるということでもあります（上にも書いた通り）。念の為注意。放射性物質の中には人間や動物の身体の特定の部分に溜まってしまうもの（人間や動物がその場所に集めてしまうもの）があります。そういう物質はせっかく崩壊して減っても、また集めてしまうことで危険性が増えます。人間の甲状腺にヨウ素が集まりやすいことや、骨などにストロンチウムが集まりやすいことがその例です。こういう「なんらかの理由で集まってしまうもの」については注意が必要です。

　以下はアタリマエのことなのですが、そこを理解せずに怖がっている人もいるようなので念の為に追加します。もう一つ我々にとってのグッド・ニュースは、「放射性物質は（作られない限りは）増えない」ということです。上で見せたように、放射性物質は壊れる（崩壊する）ことで放射線を出します。この放射線が人間の身体に当たることによって健康に害を与えるのですが、放射線を出せば出すほど、放射線を出す能力（放射能）を失っていくのです。これは、病気の原因であるウィルスや細菌が（条件が彼らにとってよければ）どんどん増殖するのとは全く違う性質です。

　だから、平穏な状態に戻った後であれば、「いったん放射線にさらされたところにはもう入れない」と怖がる必要はありません。ちゃんと検査して「もう放射性物質は人間に害を与えないぐらい少なくなった」ということを確認した上でなら、入れます（もちろん、検査と確認は慎重に！）。

FAQその１

「半減期で半分なくなるんなら、半減期の２倍で全部なくなるんじゃないんですか？？」

と思いたくなりますが、それは違うのです。

　なぜこうなるかというと、放射性物質かそうであるかに限らず、原子や原子核は（同じ種類であれば）個性というものがないからです。特に人間や生物の持つ個性の一つである「年齢」がありません。だから、「年取って今にも崩壊しそうな放射性元素」も「若いからまだまだ崩壊しない放射性元素」もいません。みんな等しく、同じ確率で崩壊します。だから、数が多ければ多い分だけたくさん崩壊します（数が少なければ比例して崩壊数も少ない）。というわけで、半分になるまでの時間が一定になるのです。

　「放射性物質がいつ崩壊するか？」は確率で決まる現象です。半減期は「これだけ経過したら、すでに崩壊している確率が５０％だ」という時間です。確率的な現象だから、運がいいと（悪いと？）崩壊する数が50%より多いこともあるし、逆に50%より少ないこともあります。

　実際、上のプログラムを実行してみると、100個から始めて半減期に達した時に、常に50個になるかというとそうはなりません（やるたびに数がばらつくはず）。

　ただし、実際の放射性物質の場合では（そもそもの数が膨大なので）、この確率的な「ばらつき」は（全体の数の比率では）小さくなります。

FAQその２

「次に崩壊する原子は予想つかないんですか？」

　つきません。これは上に書いた通り、「原子には年齢という個性がない」ので「今にも崩壊しそう」とか「まだまだ大丈夫」と判断できるような違いも持っていないのです。
　崩壊は、確率的に（というよりも確率的にだけ！）決まります。

FAQその３

「で、いったいいつになったら０になるんですか？？」

と、聞きたくなる気持ちはわかるんですが、それは簡単にはわからないのです。
　上で説明したように半減期ごとに（確率的に）半分になっていきますが、最初が100個なら半減期で50個、半減期×２で25個、と割り算していくと、半減期×７で0.78125個になります。
　ということは、（たぶん確率的に）半減期×７ぐらいで0になるはずです（実際、上のプログラムでもそのあたりで0になるはず）。

　しかし、最初が1000個だったら、だいたい半減期×10ぐらいで0になるでしょう。つまり、最初の量がどれくらいかで「０になる時間」は違います。そして、実際に0になる時間は（上の二つのFAQでも説明したように）確率的にしかわかりません。

　ちなみに、今ここに131gのヨウ素131があったとすると、その原子の数は

600000000000000000000000個

ぐらいです。これはだいたい半減期×79という時間で0になります（意外と速い？）。

　なお、実際に0にならなくても、出てくる放射線の量がどんどん弱くなっていきます（半減期×10で元の1000分の１ぐらいになってしまう）。

ホームページに戻る