経路積分とは何か?(Applet同梱版)その3
前野[いろもの物理学者]昌弘
下のプログラムがうまく動かない、という人はSUNのjavaの広場のページにいってjavaをダウンロードしてインストールしてみてください。
「Download Now!」と書いてある横のボタンをクリックすればダウンロードできます。
・物質は波か?粒子か?(屈折を使って重力を表現する)
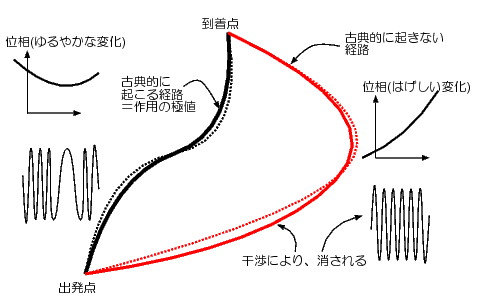
光から物質へと目を移そう。古典力学においては「物体は作用が最小となる経路を通りたがる」と表現される「最小作用の原理」が存在する(これまた初学者に「粒子はなぜ作用が最小になる道を知っているのか?」と疑問を起こさせる神秘的な“原理”である)。量子力学の黎明期である1923年、ド・ブロイはここに目をつけて、フェルマーの原理が光の波動性で説明されるように、最小作用の原理にも波動的説明があるのではと考えた。波動光学と同様に「粒子がいろんな経路を通ると考えて全ての可能性を足し上げると、古典力学において実現する経路が残る」と考えたのである。
ド・ブロイの考え方により、力学における「作用」は波としての「位相」と結びつく。この考え方の具体的表現の一つが経路積分である。
通常の「積分」では、一つまたはせいぜい数えられる程度の数の変数(たとえばx)を変化させてその時の関数の値f(x)を足し上げていく。経路積分では変化させるのは数ではなく「関数の形そのもの」である。つまり、「出発点x_iと到着点x_fを固定して、その間をつなぐ経路の全てについて、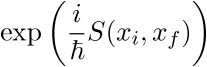 を足し上げる」という計算を行う。は作用であり、これを
を足し上げる」という計算を行う。は作用であり、これを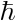 という定数で割ったものが物質波の位相となる。位相(ひいては作用)が最小となる経路が、古典力学的に実現する(干渉で消されることがない)経路である。
という定数で割ったものが物質波の位相となる。位相(ひいては作用)が最小となる経路が、古典力学的に実現する(干渉で消されることがない)経路である。
たとえば物体が重力場中で放物運動する場合について、以下で考えよう。作用は「運動エネルギー引く位置エネルギー」と書かれることが多い。落体の運動においては、
・物体が低いところを通ると、位置エネルギーが減るので作用は大きくなる(作用が「運動エネルギー引く位置エネルギー」であることに注意)。
・物体が高いところを通ると、運動エネルギーが増える(同じ時間で遠くまで行くのだから速くなくてはいけない)ので作用は大きくなる。
というバランスがあり、高いところを通っても低いところを通っても作用が大きくなる。つまりどこかに「最小作用」の軌道があり、それが運動方程式の解である。
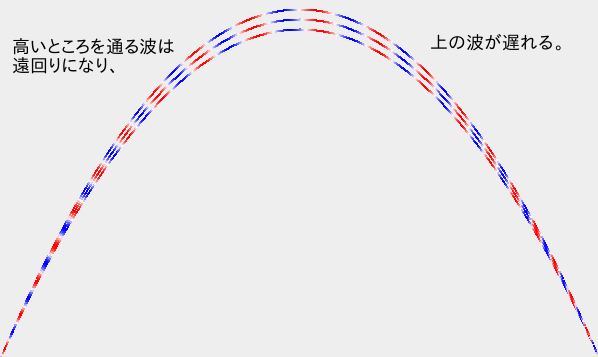
物体を波動と考える立場では、「高いところでは波長が長くなり、低いところでは波長が短くなる」という作用があるとする(これはある意味エネル
ギー保存則である。ド・ブロイによれば、運動量が大きいと波長が短い)。すると、
・波が低いところを通ると、波長が短くなるので位相が大きくなる(距離による位相は2π÷(波長)×距離であることに注意)。
・波が高いところを通ると、距離が長くなるので位相が大きくなる(同上)。
というバランスがあり、高いところを通っても低いところを通っても位相が大きくなる。つまりどこかに「最小位相」の経路がある。
以下で重力場中での「物質波」をアニメーションで見よう。
・クリックすることで、最高点の高さを変えられます。
・スライダで波長を変えられます(短めにした方がわかりやすいでしょう)。
古典的運動より高いところを通る場合。
 のようになって、この3つの波が消し合ってしまう。
のようになって、この3つの波が消し合ってしまう。
古典的運動より低いところを通る場合。
 のようになって、やはりこの3つの波は消し合ってしまう。
のようになって、やはりこの3つの波は消し合ってしまう。
古典的運動(上二つの中間)
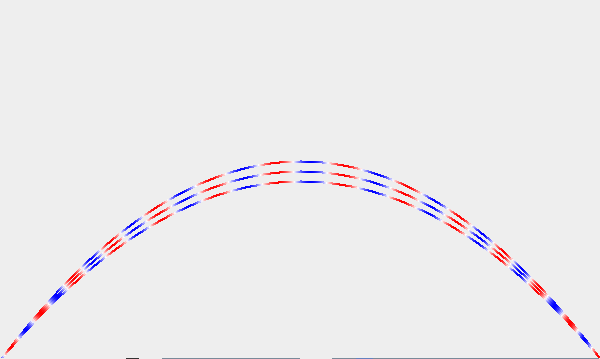 となるのが、ちょうどよいところ。この場合、3つの波はほぼ強めあう。
となるのが、ちょうどよいところ。この場合、3つの波はほぼ強めあう。
こうして、「古典的運動」つまり我々が普段観測している運動は、「いろんな波を足し算した中の、互いに干渉によって消し合わなかった波の進路」なのだということがわかる。つまり「物が落ちる(重力にひっぱられる)」という現象も、一種の屈折なのである。古典力学での「力」は「物体に加速度を生じさせるもの」であったが、量子力学におけるそれは「波長の変化を生じさせるもの」ということになるだろう。
実際の経路積分の計算はけっこうややこしい。ここではイメージだけを図示しよう。
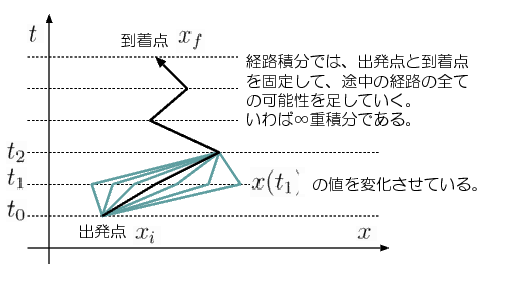 ←ほんとは、これもアニメーション作りたい。そのうち作るから待ってて(^_^;)。
←ほんとは、これもアニメーション作りたい。そのうち作るから待ってて(^_^;)。
我々が普段物質の波動性に気づかないのは、物質波の干渉による消し合いがほぼ完璧だからである(ニュートンが光が波だと気づかなかったのと同様、波長が短すぎるのが原因)。「ほぼ」だが完璧ではなく、特にミクロな現象では、古典力学とは差が出てくる。そして、経路積分(量子力学)の方が正しく現象を予言するのである。
このように考えていくと、ド・ブロイが物質の波動論を唱えた後、建設されるべき量子力学の形式は経路積分であるべきではなかったのか、という思いすらする(実際にはド・ブロイのアイデアを最初に数学的に実現させたのはシュレーディンガーであり、その結果が彼の名のついた方程式である。経路積分の登場は少し遅れる)。実際にどのように経路積分という計算が実現するのかは、ファインマンの教科書(「量子力学と経路積分」ファインマン&ヒッブス(みすず書房))をひもとくのがいいだろう。

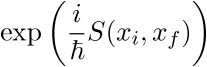 を足し上げる」という計算を行う。は作用であり、これを
を足し上げる」という計算を行う。は作用であり、これを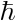 という定数で割ったものが物質波の位相となる。位相(ひいては作用)が最小となる経路が、古典力学的に実現する(干渉で消されることがない)経路である。
という定数で割ったものが物質波の位相となる。位相(ひいては作用)が最小となる経路が、古典力学的に実現する(干渉で消されることがない)経路である。 のようになって、この3つの波が消し合ってしまう。
のようになって、この3つの波が消し合ってしまう。 のようになって、やはりこの3つの波は消し合ってしまう。
のようになって、やはりこの3つの波は消し合ってしまう。 となるのが、ちょうどよいところ。この場合、3つの波はほぼ強めあう。
となるのが、ちょうどよいところ。この場合、3つの波はほぼ強めあう。