経路積分とは何か?(Applet同梱版)その2
前野[いろもの物理学者]昌弘
下のプログラムがうまく動かない、という人はSUNのjavaの広場のページにいってjavaをダウンロードしてインストールしてみてください。
「Download Now!」と書いてある横のボタンをクリックすればダウンロードできます。
・屈折も干渉の結果である
ホイヘンスの原理以外に、光の進む道を決める原理としては、「フェルマーの原理(光は最短距離を通りたがる)」がある。この原理を初めて聞いた人は皆、「光はいかにして最短距離を知ることができるのか??」と不思議に思う。光が最短距離を“選択”するメカニズムは、最短距離だけが「干渉によって消されない」からなのである。「最短」ということは、その付近で距離、ひいては位相(「位相」というのはいかめしい単語であるが、sinθやe^iθのθのことであり、波の式がy=A sin(kx-ωt)ならば kx-ωtのこと。このようにして距離や時間と関係する)の変化がゆるやかになっている。ほとんどの光が消し合う中、最短距離を通ってきた光だけが強め合う。下の図は屈折の法則をこの考え方で表現したものである。空気中のA地点から水中のB地点へ到着する光は、ありとあらゆる経路を通っている。しかし、我々が観測する光は、消し合うことがなかった特別な道を通ってきたものだけである。
・屈折の法則を示したアニメーションです。
・下のスライドで屈折率を変えられます。
屈折率が1.5の時の波の様子

赤矢印で示したあたりが、強めあっている(残る)ところ。
屈折率が0.5の時の波の様子
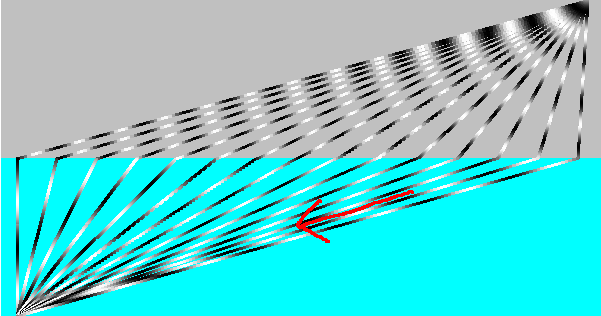
赤矢印で示したあたりが、強めあっている(残る)ところ。
もちろん、屈折率を1にすると直進が強め合う。
光の経路を知るためには、最短距離を探す必要はない。いろんな経路を通る光をとりあえず全部考えてみればよい。その全てを重ね合わせたのち、干渉によって消されない経路を通った光こそ、我々が観測する光なのである。この「いろんな可能性を全部足した後、消されずに残るものが実現する」という考え方を物質粒子にも適用するのが、経路積分の考え方である。

