Nが十分大きくなれば、この現象は「連続的に流水量を増やしていった場合」と変わらない、ということがわかるだろう。N→∞の極限を取ることを考えれば、最終的結果はグラフの下の部分(三角形)の面積となる、ということである。
数式で示しておこう。時刻tが0〜Tまで経過したとして、その時間TをNに分割しているとすると、分割の一個はΔt=T/Nである。ここで計算している水色の長方形一個の面積は
iaΔt×Δt
で、iを1からN-1まで足すことになる。
1+2+3+4+…+N-1=N(N-1)/2
という公式があるのでこの答えは
aN(N-1)(Δt)2/2=aNΔt×(N-1)Δt/2
であるが、NΔt=Tで、(N-1)Δtは「T=NΔtよりΔtだけ小さい」(ということは、N→∞でΔt→0となれば差はないも同然)と考えれば、
aN(N-1)(Δt)2/2→aT2/2
となる。これは底辺Tで高さがaTの三角形の面積そのものである。
これを積分記号を使った式でかけば、
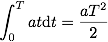
ということで、このように「刻一刻と変化していく量との掛算」に対応するのが積分なのである。