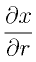 と
と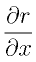 はなぜ逆数ではないのか
はなぜ逆数ではないのか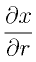 と
と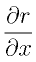 はなぜ逆数ではないのか
はなぜ逆数ではないのか 常微分なら逆数になる、「微分の上と下が入れ替わったもの」ですが、偏微分では一般にそうはなりません。
二つの偏微分
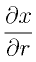 と
と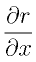
の意味の違いを、図で説明します。まず一つめの図では「rで偏微分する」ということを図で表現します。
θを一定としてrを変化させた時のΔx,Δy
作成 GeoGebra |
青い●(ベクトルの起点)はマウスで動かすことができるので、いろいろ動かしてΔr,Δx,Δyの関係をつかんでください。
この図で表現しているのは「θを一定としてrを変化させた」状況です。これは、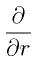 という微分に対応します。
という微分に対応します。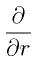 と書くときは「独立変数はrとθで、rで微分する時はθは一定だよ」と決めているのです。つまり、図の赤矢印のように、「原点から離れる方向の微分」をしています。
と書くときは「独立変数はrとθで、rで微分する時はθは一定だよ」と決めているのです。つまり、図の赤矢印のように、「原点から離れる方向の微分」をしています。
図の中のΔx/Δrの、Δrを0にする極限をとったものが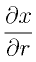 だと考えればいいでしょう。
だと考えればいいでしょう。
では次に、「xで偏微分する」を図で表現しましょう。
yを一定としてxを変化させた時のΔr,rΔθ
作成 GeoGebra |
こっちの青い●(ベクトルの起点)もマウスで動かすことができるので、いろいろ動かしてΔx,Δr,rΔθの関係をつかんでください。
これは「yを一定としてxを変化させている」ので、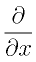 という微分に対応します。
という微分に対応します。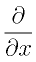 と書くときは「独立変数はxとyで、xで微分する時はyは一定だよ」と決めているのです。図の赤矢印のように、「x方向正方向(平たく言えば、「右」方向)の微分」をしています。
と書くときは「独立変数はxとyで、xで微分する時はyは一定だよ」と決めているのです。図の赤矢印のように、「x方向正方向(平たく言えば、「右」方向)の微分」をしています。
上の図と下の図では「何を一定にして何を変化させたか」が違う。つまり「微分する方向」が違うのです。
この二つで、ΔrとΔxの関係を見れば、二つの偏微分の意味がわかるでしょう。上の図でのΔx/Δrと、下の図でのΔr/Δxをよく観察してみてください。
特に、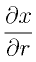 と
と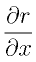 という二つの微分が(逆数ではなく)むしろ同じ値を出すものであることが納得できるのではないかと思います。
という二つの微分が(逆数ではなく)むしろ同じ値を出すものであることが納得できるのではないかと思います。