東京図書「よくわかる熱力学」サポートページ

このページは、「よくわかる熱力学」(前野昌弘著/東京図書)のサポートページです。
不明な点がありましたら、irobutsu@icloud.comにメールするか、またはサポート掲示板に書き込んでください(サポート掲示板に書き込むとメールが届くようになっています)。
「はじめに」より抜粋
熱力学の理解の筋道にはいくつかの「流儀」があるが、本書は
熱力学は「力学」の続きである
という姿勢で進めていく。
初等力学では力から「仕事」が定義され、仕事により増減する物理量として「ポテンシャルエネルギー」が定義される。いったんポテンシャルエネルギーが定義されると、逆にそのポテンシャルエネルギーを微分することで「力」がわかる。力学では「仕事によってポテンシャルエネルギーが増減」「ポテンシャルエネルギーを微分すると力」という概念が有用である。この有用な概念を熱現象が現れる場合にも広げていく。熱力学で定義される「ポテンシャルエネルギーに対応する量」のことを「熱力学関数」と呼ぶ。
熱力学では初等力学に比べ仕事が行われる状況について考慮すべきポイントが増える。それがゆえに「熱力学関数」は初等力学の「ポテンシャルエネルギー」に比べ注意深く定義していく必要があるし、後で定義するFという熱力学関数については上に挙げたポテンシャルエネルギーの性質は(特に「仕事によって増減」という部分は)非常に限定された意味でしか通用しない。それでも熱力学関数は大変有用で、「微分すると力に限らずもっといろいろな物理量がわかる」という性質はとてもありがたい。
熱力学を勉強する物理学徒の悩みは「熱とはなにか?」「エントロピーとはなにか?」という疑問であろう。その「悩み」を解消するため、まずは力学での「仕事→エネルギー」という流れの先に続く概念として(新しいものではなく「力学の思想の続きにあるもの」として)熱、そしてエントロピーを導入していこうというのが本書での流れである。このあたりの熱力学へのアプローチの仕方は『熱力学―現代的な視点から』(田崎晴明著、培風館)に準拠している。熱は目に見えないが、「力」は目には見えなくとも感じることはできるし、「仕事」は実感することができる。そのような「目に見えるもの」「操作できるもの」さらに言えば「手応えを感じられるもの」を使って熱力学という「物理」を知っていこう、というのがこの本でやりたいことだ。
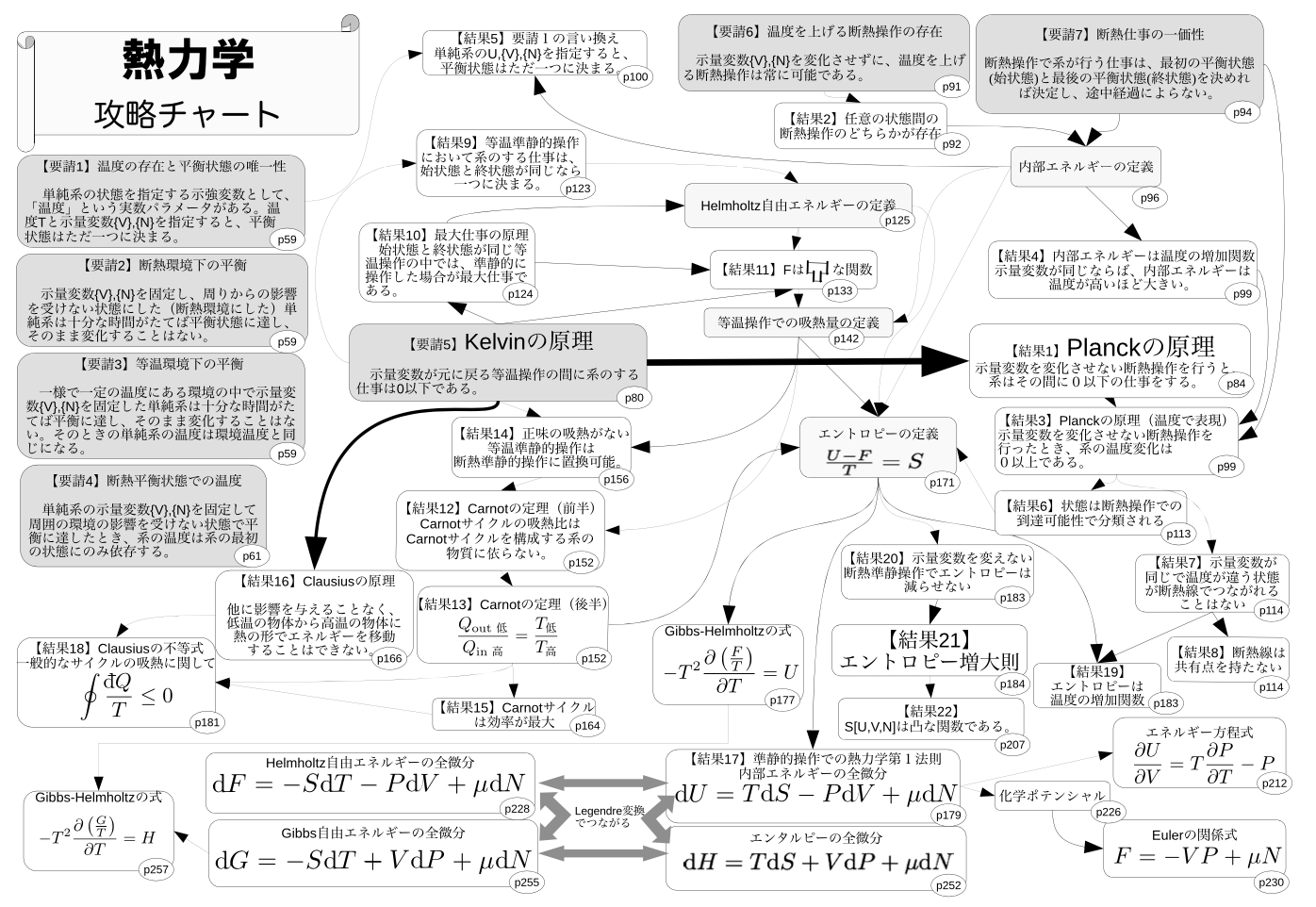
熱力学攻略チャート
本書見返しに載せた、本書における熱力学の理解の流れ図です。
ページ数が多すぎたため、章末演習問題のヒントと解答はPDFにて配布することにしています。こちらからダウンロードしてください。
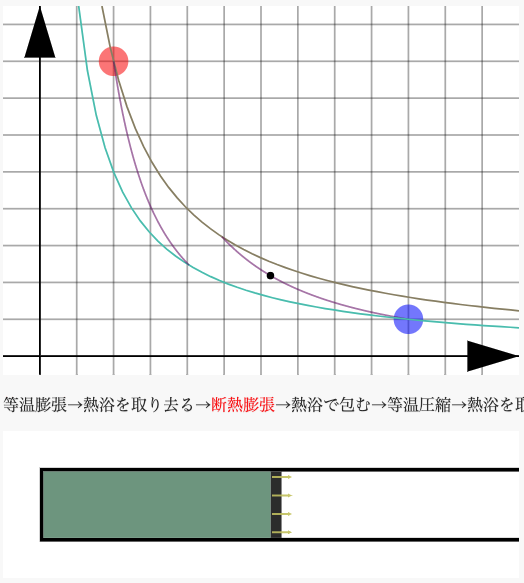
「よくわかる熱力学」の図に使われているシミュレーションプログラム(Javascriptによるもの)をこちらに掲載しています。アニメーションして動くグラフや図を見ることで、物理の理解は飛躍的に進みます。是非活用してください(「よくわかる熱力学」を持っていなくても、これらのプログラムを使って学習することは可能です)。
↓一例:Carnotサイクル
wikiです。感想・質問などお寄せ下されば。
・ネット書店の売り場へのリンク
$$\definecolor{hai}{RGB}{137,137,137}\def\haiiro#1{{\color{hai}#1}}$$
・出版後に発見された内容のミスについて
$$\newcommand{\kakko}[1]{\!\haiiro{\left(\kuro{#1}\right)}}$$
$$\newcommand{\Kakko}[1]{\!\haiiro{\left[\kuro{#1}\right]}}$$
$$\def\diff{\mathrm d}$$
$\def\kuro#1{{\color{black}#1}}\newcommand{\PDC}[3]{{\opcol{\left(\kuro{{\partial {#1}\over \partial #2}}\right)}}_{\!\!#3}}\def\opcol#1{{\color{Gray}#1}}$
以下に、発見されたミスを記載していきたいと思います。
これらの訂正部分のうち、数式・図版などを実際の本とほぼ同サイズになるように印刷できるPDFファイルがこちらです(ただし、簡単な文字の訂正などは含まれていません)。こちらをダウンロードして切り貼りしてくださってもよいです。
- p67の脚注†63の後に脚注†64として「James Prescott Jouleはイギリスの物理学者。日本語読みは「ジュール」。Joule熱もそうだが熱と仕事の変換についても仕事をしている。SIのエネルギーの単位 J の由来となっている。」を挿入。
- p70の一番下の行「準静的で」を「準静的に」に訂正。
- p165の【問い8-5】の図がおかしなことになってます(印刷工程上でのミスです)。正しい図は以下の通り。

- p182の下から6行目の「定義された5.5.2項」を「定義されたエントロピーは、5.5.2項」と訂正。
- p188の(9.44)の2行下にある「つまり${\mathrm d}W$を」(dにはバーが付いてる)を「つまり$\mathrm dV$を」に訂正。
- p197の図中、矢印内の(2)と(3)が逆(今(2)のある場所に(3)、(3)のある場所に(2))これも印刷工程でのエラー。
- p242の一番上の式の真ん中の$P_{\mathrm AB}$の前の符号は$+$ではなく$-$。
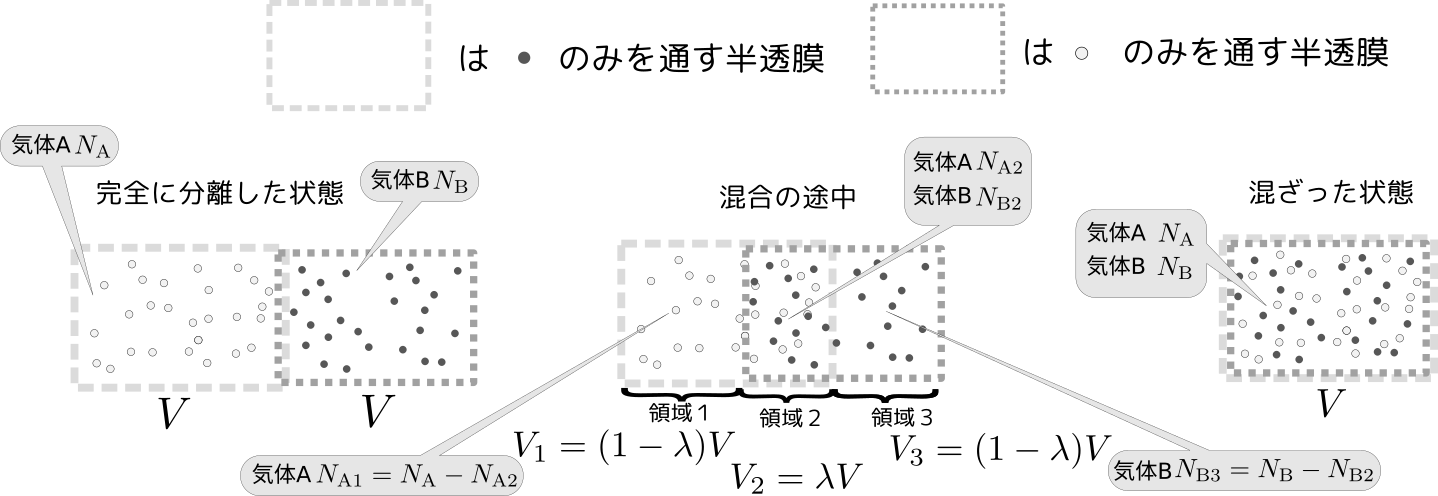
- p242の11.3.5項の5行目(図の真上)「Aのみを」を「Bのみを」に訂正。
- p254の一番上の行の$U(T;N)=cNRT$を$U(T;N)=cNRT+N\mu$に訂正。
- p279の13.3項の10行目の「X'X→Y'」を「X'→Y'」に訂正。
- p285の脚注22の「密度が」を「体積が」に訂正。
- p286の(13.27)の左辺$\Delta S_{\rm mix}$を$- \Delta S_{\rm mix}$に訂正。
- p296の(14.2)の3行下、「${\rm H}_2{\rm O}$が増える」を「${\rm O}_2$が増える」に訂正。
- p303の(14.26)式の下の$K(P)$は$K(T)$に訂正。
- p303の(14.26)式より3行下にある$\mu(T;P_0)$は$\mu(T,P_0)$に訂正。
- p303の脚注25の3行目冒頭の$\nu$を$\mu$に訂正。
- p309の一番上の行にある式に3回現れる$T;P,N$を$T,P;N$に訂正。
- p340の下から2行目の$N_{\rm A}$と$N_{\rm B}$をそれぞれ$N_{\rm A1}$と$N_{\rm B1}$に訂正。
- p353の(B.108)に2回現れる${T_2\over T_1}$を${T_1\over T_2}$に訂正。
- p360の(B.155)のlogの中身の${RT^{c+1}\over P}$を${RT^{c+1}\over \xi P}$に訂正。
- p368の(B.216)は
$$
\begin{align}
U\kakko{x_0+\Delta x,y_0+\Delta y}
=&\int_{x_0}^{x_0+\Delta x}P\kakko{x,y_0}\diff x +\int_{y_0}^{y_0+\Delta y}Q\kakko{x_0+\Delta x,y}\diff y
+U\kakko{x_0,y_0}
\nonumber\\
=&P\kakko{x_0,y_0}\Delta x +Q\kakko{x_0+\Delta x,y_0}\Delta y+U\kakko{x_0,y_0}\nonumber\\
=&P\kakko{x_0,y_0}\Delta x +Q\kakko{x_0,y_0}\Delta y
+{\partial Q\kakko{x_0,y_0}\over \partial x}\Delta x\Delta y+U\kakko{x_0,y_0}
\end{align}
$$
と訂正(右辺第1項の積分の上限と、右辺の全てに$+U\kakko{x_0,y_0}$を追加)。
さらに、(B.217)の最後にも$+U\kakko{x_0,y_0}$を追加。
ここより下のミスは第4刷で訂正されました。
- P351の(B.86)の第1項の偏微分において一定とする量はS,NではなくT,Nです。$\PDC{F\Kakko{T;V,N}}V{T,N}$となります。
ここより下のミスは第3刷で訂正されました。
ここより下のミスは第2刷で訂正されました。
- p16の2.1.3項の6行目「BがAにされる仕事」を「BがAにする仕事」に訂正してください。
- p38の(2.49)の第2項の分子の$\partial V$となっているところを$\partial U$に訂正。
- p155の(8.6)の右辺を$Q\haiiro{(}T_高;V_{\scriptscriptstyle 高小}\to V_{\scriptscriptstyle 高大}\haiiro{)} + \alpha \underbrace{Q\haiiro{(}T_高;v_{\scriptscriptstyle 高大}\to v_{\scriptscriptstyle 高小}\haiiro{)}}_{-Q\haiiro{(}T_高;v_{\scriptscriptstyle 高小}\to v_{\scriptscriptstyle 高大}\haiiro{)}}$と訂正(高小と高大の順番が逆だった)。
- p160の(8.13)の右辺の分母と分子が逆です。
- p167の図がおかしくなっていました。正しくは以下の通りです。
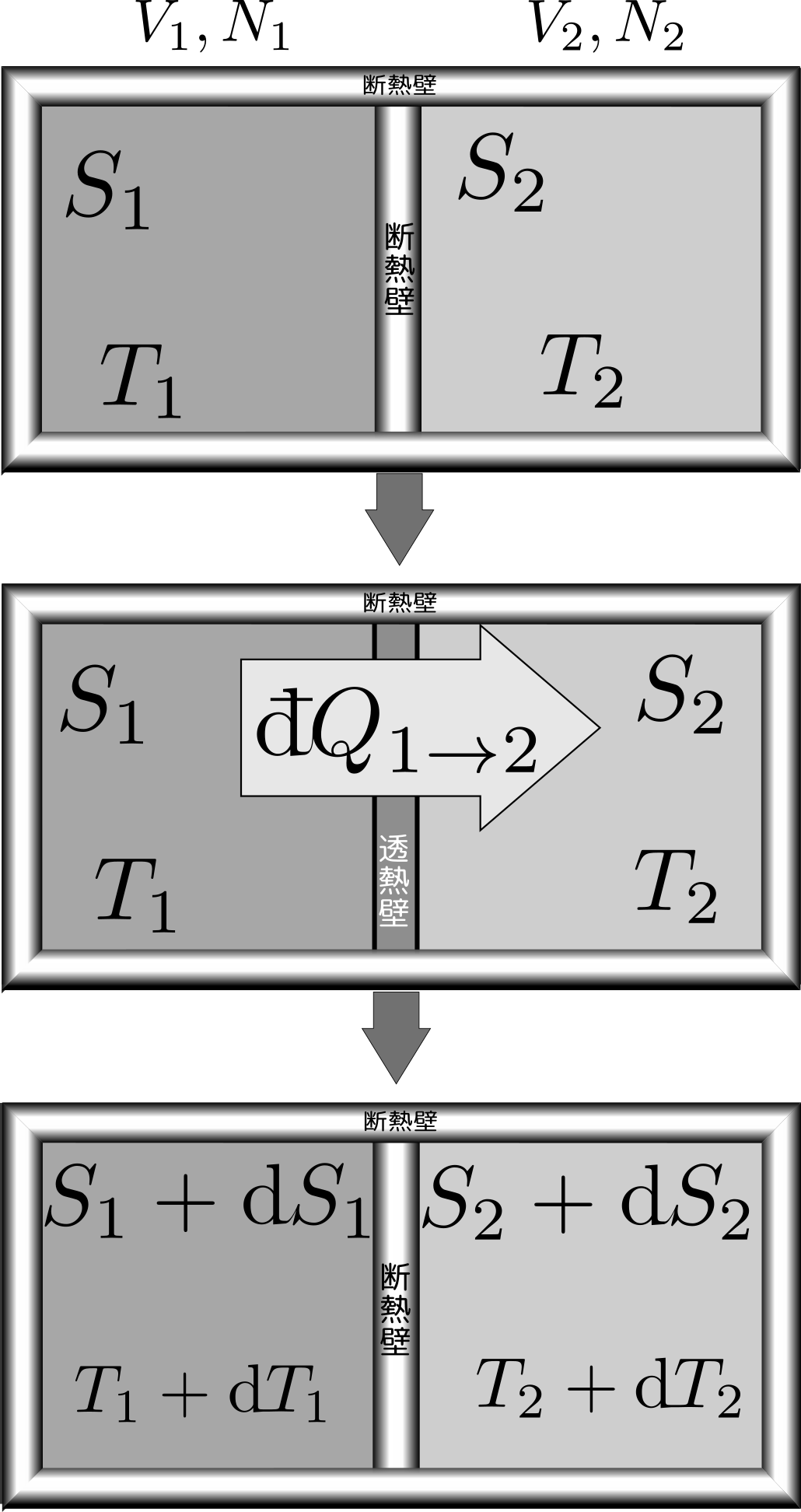
- p191の図の中で「透熱壁」と「断熱壁」の文字が入れ替わってました。正しくは以下の通りです。
- p229の練習問題の2行上の「\(N\)という示量変数に応じてのエネルギー変化の割合」を「\(N\)という示量変数の変化に応じてのエネルギー変化の割合」と訂正。
- p242の(11.39)の第2項が$V$による微分になっていますが、$V_{\rm AB}$による微分が正しいです。
- p246の(11.42)と(11.43)を以下のように訂正。
$$
F_前\haiiro{[}T;V,N\haiiro{]}=F_0\haiiro{[}T;V,(1-x_前)N\haiiro{]}+F_1\haiiro{[}T;V,x_前 N\haiiro{]}
$$
$$
F_後\haiiro{[}T;V,N\haiiro{]}=F_0\haiiro{[}T;V,(1-x_後)N\haiiro{]}+F_1\haiiro{[}T;V,x_後 N\haiiro{]}
$$
- p295の脚注†6の最後の式は$\epsilon={X-X_{\rm min}\over X_{\rm max}-X_{\rm min}}$が正しいです。
- p303の(14.26)の2行下と、【問い14-2】の1行目の$K\haiiro{(}P\haiiro{)}$は$K\haiiro{(}T\haiiro{)}$に訂正してください。
- p303の【問い14-2】の最後の句点の前に「(今は理想気体を考えているので、$\mu_i\haiiro{(}T,P_0\haiiro{)}$は物質量にも$X$にも依らないことに注意)」を追加。
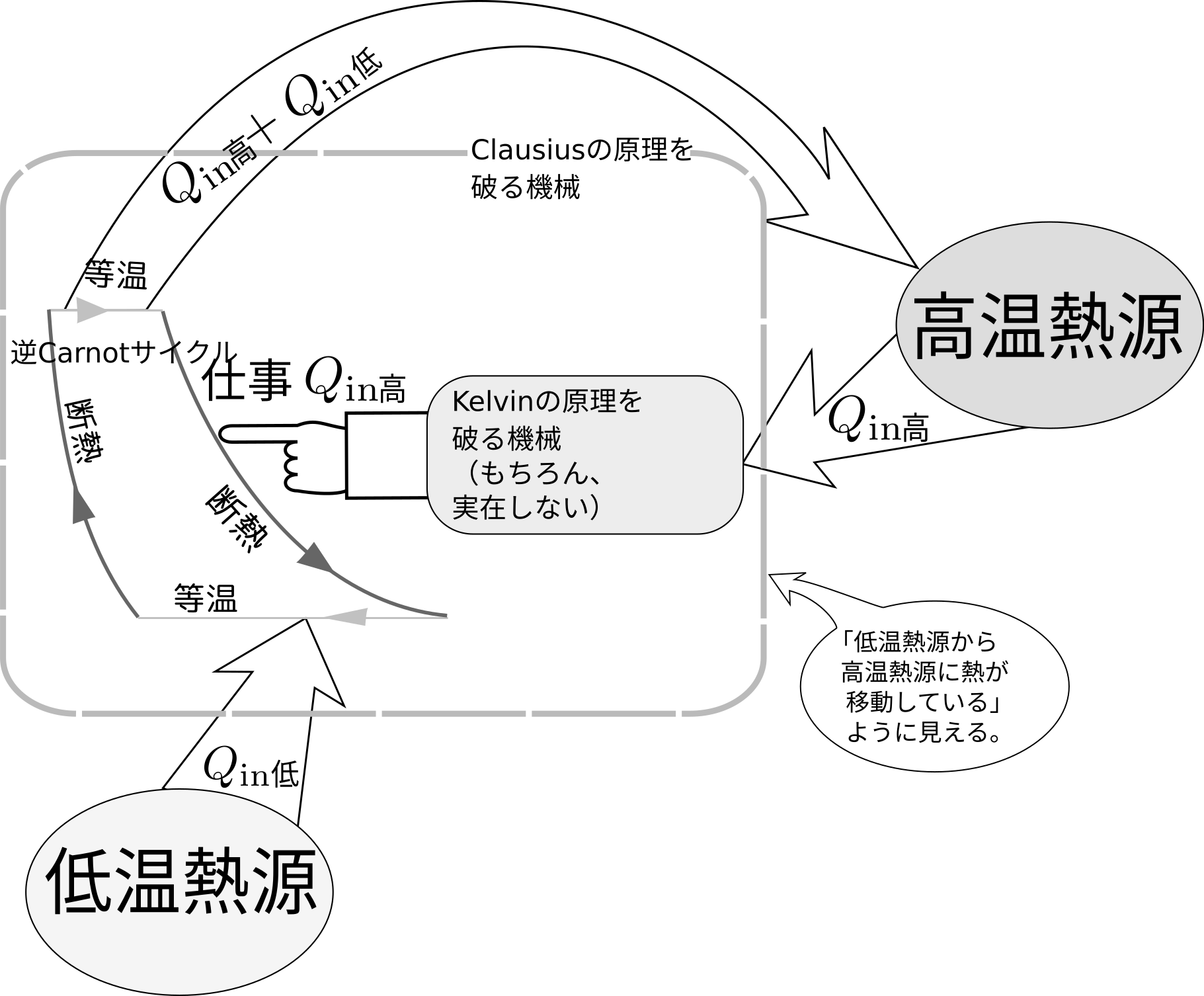
- p339の【問い8-3】のヒントの2,3行めの$-Q_{\rm out低}$と$-Q_{\rm in 高}$のマイナス符号を取り、最後から2行目の$Q_{\rm in高}-Q_{\rm out低}$を$Q_{\rm out低}-Q_{\rm in高}$に訂正。
- p349の【問い8-2】の解答、(B.73)と(B.77)の左辺を${Q_{\rm out低}\over Q_{\rm in高}}$に変更。
- p349の【問い8-3】の解答の1行目の式を${Q_{\rm out 低}\over Q_{\rm in高}-Q_{\rm out低}}= {1\over {Q_{\rm in高}\over Q_{\rm out低}}-1}$に訂正(分母分子の符号を両方変えるので、答は同じですが)。
- 裏見返しの下の「完全な熱力学関数の全微分」の式のうち、$\mathrm d F$と$\mathrm d G$の式で$\mathrm d S$となっているところは$\mathrm d T$の誤りです。
書籍サポートページの目次に戻る