よくわかる電磁気学サポート掲示板4
この前の電流の位置エネルギーの質問 †
大学生? (2018-03-29 (木) 00:56:50)
この前、御教授いただいたように、仮想変位を考えるやり方でエネルギーから力を算出しようとしたのですが、うまくいかない問題がありました。
それは、2つの電流回路の問題です。
ここでは力が、I_1・I_2・grad(L_12)となります。(ベクトルポテンシャルを用いずに磁場を使って計算した。)
ベクトルポテンシャルを用いた場合と逆符号となってしまいます。
なぜ、エネルギーが増える方向に力が働く結果となるのですか?いつでもベクトルポテンシャルから力が計算できる訳では無いのでしょうか。
- L_12は電流回路の相互誘導係数です。 -- 大学生?
- ベクトルポテンシャルで計算しても、磁場同様「平行電流は引力」という結果になりませんか?? そのあたりの計算は228ページで図解してます。 -- 前野?
- そうするとポテンシャルがどんどん増えていきませんか? -- 大学生?
- そうするとポテンシャルがどんどん増えていきませんか? -- 大学生?
- 同じ方向の無限直線電流も近づけば近づくほどポテンシャルは高くなりませんか? -- 大学生?
- エネルギーは$-\vec j\cdot \vec A$ですよ(マイナス符号に注意)。 -- 前野?
- jとAが同じ向きなら、エネルギーが低くなるのはポテンシャルが高くなる方です。 -- 前野?
- そうでした。本当にごめんなさい。 -- 大学生?
- ベクトルポテンシャルから導いたエネルギーと、静磁場のエネルギーがH・Bd³ xであることから導いたもので符号が逆になると思うのですが、ベクトルポテンシャルから導いた方が正しいのでしょうか。 -- 大学生?
- その違いについてはこちらに書いてありますので読んでください。その二つのエネルギーは使い所が違うのです。 -- 前野?
- 貼ってくださったurlを見て勉強しています。コンデンサーのルエネルギーのジャンドル変換の数学的解釈で主張していることがよくわかりません。 -- 大学生?
- 私が解釈するには、電池を繋いでいない時と繋いでいるときでは全エネルギーの表式が異なるので、U₁ とU₂で区別をする。区別はするものの、Cを変えたときの手の仕事は一緒になると予想し、U₁ をQ固定でCで偏微分したものと、U₂ をV固定でCで偏微分したものが同じになるようにルジャンドル変換をほどこした。 というように思えます。しかしながら、かなり間違った解釈だと思えてなりません。前野先生の考えをしっかり理解したいです。どこが根本的に間違っているか、指摘いただきたいです。 -- 大学生?
- コンデンサが電池につながっている場合、二つの間でエネルギーの流れがあるのだから、エネルギーの合計が保存する、そのため正しい計算を行う為には電池のエネルギーQVを足しておかなくてはいけない、というのが物理的理由で、その「電池(外部)のエネルギーを足しておく」という操作がルジャンドル変換という数学的操作と一致します。 -- 前野?
- 「同じになるようにルジャンドル変換を行った」というのは間違ってはいません。その操作を行うことがつまり「外部にあるエネルギーをちゃんと考えた」という物理的考察に一致しているわけです。 -- 前野?
- 「手の仕事が」同じになるようにルジャンドル変換を行うということで良いのでしょうか。仕事が等しくなるのが直感的にわかりません。 -- 大学生?
- 仕事が等しくなる、というよりは「電荷のクーロン力が等しくなる」ということですが、これは「なるように」なんてしなくても同じに決まってます(同じ電荷が同じ配置になっているんだから)。 -- 前野?
- 力(あるいは仕事)が同じになるのは「物理的に同じ状況だから」で、物理が決めてます。一方、「力はエネルギーの微分で与えられる」ということがあります。「電荷Qが一定」という条件での微分と「電圧Vが一定」という条件での微分は違う微分なので、どちらの条件の場合でも「エネルギーを微分したら力」になるためには、それぞれの条件に応じてエネルギーを変えます。 -- 前野?
- よくわかりました。ありがとうございました! -- 大学生?
電流の位置エネルギー †
大学生? (2018-03-14 (水) 15:33:12)
電流の位置エネルギーが-j↑・A↑とあるのですが、これの-gradをとっても電流にかかる力j↑×rotA↑の式にならなくないですか?
余分な項(j↑・grad)A↑がでてきてしまい、それを電流の全部分について積分したとしても上手く消えないとおもいます。
- ああ、その計算では力にならないです。たとえば静電エネルギーに電荷を掛けたqVは、gradを取るとgrad V=-Eのおかげで-qEになってクーロン力になりますが、これはつまり、ある場所$\vec x$にいる電荷qのエネルギー$qV(\vec x)$とそれよりちょっと違う場所にいる電荷qのエネルギー$qV(\vec x+\Delta \vec x)$の差を取るという物理的意味のある計算をやってます($\Delta \vec x\cdot{\rm grad}\left(qV(\vec x)\right)=qV(\vec x+\Delta \vec x)-qV(\vec x)$)。 -- 前野?
- つまり「電荷を仮想変位させて、そのときの仕事が力掛ける$\Delta x$になる」ということで微分と力が結びついているわけです。ですから電流に働く力を考えるときは、「電流を仮想変位させる」という操作が要ります。 -- 前野?
- 電流の変位は単に「場所$\vec x$をずらす」ような操作ではなく「電流路の変形」が必要になります。下の図のような感じです。 -- 前野?
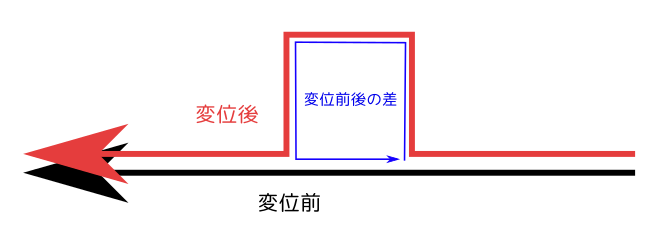
- この「電流の仮想変位」では、電流の強さ$I$は変えないことにします。また、電流は線上にしか存在しないので、位置エネルギーは$I\vec A$の線積分になります。すると図に書いた「変位前」と「変位後」で線積分の結果の差は図に「変位前後の差」と書いた長方形の上で$I\vec A$を線積分した量になります。 -- 前野?
- 電流は一定値で線積分の外に出るとすると、$I\oint \vec A\cdot \mathrm d\vec x$という線積分を行えばよいのですが、ストークスの定理により$\oint \vec A\cdot \mathrm d\vec x=\int ({\rm rot}\vec A)\mathrm dS$と、rot Aつまり磁束密度Bの面積積分になります。 -- 前野?
- こうして仮想変位による仕事は、「電流$I$×紙面に垂直な方向の磁束密度×(変位前後の差の部分の面積)」となります。これを変位させた距離でわると電流に対するローレンツ力になりますので、確認してみてください。 -- 前野?
- お返事、ありがとうございます。丁寧でわかりやすいです。微小電流と同じ方向に仮想変位する場合はどうなるんですか? -- 大学生?
- その場合は力が0です。 -- 前野?
- しばらく考えたらよくわかりました。物理の面白さを実感しました。ありがとうございます。 -- 大学生?
p181 練習問題について †
竹村? (2018-02-26 (月) 18:39:53)
互いに並行ではない電流I1,I2に対して
BはF1×F2の方向を向くとなっていますが
I1,I2が同一平面上にない時の誤りではないでしょうか?
同一平面上にある場合は、F1//F2となり外積が0になってしまいます。
- この話は「ある場所」での$\vec B$を電流を使って測定する話なので、電流はある一点を通過してないといけません(共有点を持っていなくてはいけません)。 -- 前野?
- 同一平面上にあっても、$\vec I_1$と$\vec I_2$が違う方向を向いていれば、$\vec F_1$と$\vec F_2$は平行になりません。 -- 前野?
- 続けて申し訳ありません -- 竹村?
- I1かつI2かつ実際に求めるBが同一平面上であった場合はFが並行になってしまうのですが、現実的にはそのようなことはまず起こらない(少しは必ずずれる)ということで宜しいでしょうか? -- 竹村?
- $I_1$と$I_2$は試験電流であり、つまり「磁束密度を測定するために実験者が用意するもの」です。ですからそうならないような試験電流を用意すればよいです。-- 前野?
- 丁寧なご解説有難うございます。疑問が解決しました。 -- 竹村?
電場と電位について †
ss? (2018-02-23 (金) 15:43:28)
電場と電位の関係について質問があります。
点A:電位Vの面、点B:電位V+ΔVの面とし、AからBに電場E、変位Δsとします。このとき、ΔV<0であり、AからEΔs>0減った結果、Bとなるので、V―EΔs=V+ΔV
∴E=‐gradV
次に、点A:電位V+ΔV、点B:電位Vとし、AからBに電場E、変位Δsとします。このとき、ΔV>0であり、AからEΔs>0減った結果、Bとなるので、V+ΔV―EΔs=V
∴E=+gradVとなってしまいます。何がいけなかったのでしょうか?
書籍内の位置エネルギーとの関係から求めるやり方は理解できたのですが、上でのやり方では間違いなのでしょうか?
- 後半部分が間違ってますが、ΔVとΔsの方向を合わせてないので、ΔV÷Δsが微分になりません。A→Bへの移動をΔSと表現したのなら、A→Bでの電位の変化をΔVにしないと、微分の定義に合致しません。 -- 前野?
- お答えいただきありがとうございます。確かに、2番目のやり方もBからAへの変位をΔsとすれば上手くいきました。しかし、ある本でA:V+ΔV、B:Vとし、また、AからBへ電場E、変位Δsとして 内積E·Δs=EΔs=―ΔV(ポテンシャルが下がるため)としていました。ΔVとΔsの方向が一致していませんが、E=-gradVとなっているのは偶々なのでしょうか? -- ss?
- その本の事は知りませんが、ーΔVとしているところで調整されているという事だと思います。 -- 前野?
P129,p130 †
大学生? (2018-02-19 (月) 03:11:14)
ふたつの電荷に対してマクスウェル応力の導出がなされています。
電荷に働く力について、砂川電磁気学では、面を電荷をかこむ任意の閉曲面にとっても良いとしています。前野さんの本では閉曲面を無限に大きな球面に置いたのでしょう。前野さんは閉曲面をどうして任意にとっても良いと考えられますか。つまり、電荷が入った閉曲面であれば応力を面積分した値は、面のとりかたによらないず一意であることはどう理解できるのですか。
これがなければp127とp128で応力をエレガントに導出したことが無駄になってしまうと思います。せっかく応力を簡単に出せたのに、面全体にかかる力が面の選び方によって違ってしまったら応力を利用した力の計算ができず、結局クーロンの法則やらで力を計算するしかなくなってしまいます。
- もちろん、面の選び方にはよりません。今やっているのは静電場なので、各点各点で力はつりあいの状態にあります。そのつりあいはクーロン力と、電荷のある場所には「電荷をその場所の保持する力」を合わせて成り立ってます。電荷のない場所については静電気力だけでつりあいが達成されていなくてはいけません(そして、面のとり方で変わってしまったらつりあってないことになります)。 -- 前野?
誘導電場と相対論について †
高校教諭? (2018-02-07 (水) 17:19:38)
マクスウェル方程式によると、半径rの円の内側を貫く磁束が変化するとき、それを妨げる向きの磁束をつくろうとする起電力が生じ、それに伴って、円周上には誘導電場が生じることになりますが、磁束の変化が円の中心付近の小さい領域で起きたとしても、円周上には直ちに誘導電場が生じることになるようです。(rotB=-dE/dtより 微分は偏微分です)これは磁束の変化の情報がただちに円周に伝わるのであれば相対論の考えに反するように思えます。それとも、磁束を変化させるということは、ローカルなことではないのでしょうか。よろしくお願いします。
=
- 今非常に忙しい時期なので返事が遅れてすみません。というわけで簡潔に結論を言いますと、小さい領域で起きたときの電場の変化は光速で伝わるので、「相対論に反する」なんてことは起こりません。 -- 前野?
- 円の中心付近に置かれた小さなコイルに電流が流れて、それにより磁場が変化して誘導起電力として電場が変化していく、という状況で何が起こるのかを見るために、マックスウェル方程式から電流と電場の関係を作ることにします。まず${\rm rot}\vec E=-{\partial \vec B\over \partial t}$という式の両辺のrotを取ります。${\rm rot}~{\rm rot}\vec E=-{\partial {\rm rot}\vec B\over \partial t}$になりますが、 ここで${\rm rot}\vec B={\mu_0}(\vec j+\varepsilon_0{\partial \vec E\over \partial t})$という式(真空中で考えます)を代入します。-- 前野?
- 左辺は${\rm rot}~{\rm rot}\vec E={\rm grad}~({\rm div}\vec E)-\triangle \vec E$になりますが、${\rm div}~\vec E={\rho\over\varepsilon_0}$で電荷ρは忘れることにしましょう。 -- 前野?
- 右辺は${\mu_0}({\partial \vec j\over\partial t}+\varepsilon_0{\partial^2\vec E\over\partial t^2})$となります。 -- 前野?
- これで$(\mu_0\varepsilon_0{\partial^2\over\partial t^2}-\triangle)\vec E=-\mu_0{\partial \vec j\over\partial t}$という式ができますが、これは$\vec E$が${\partial \vec j\over\partial t}$を源として光速で伝播する波だということを表す式です。 -- 前野?
- つまり小さいコイルに流れる電流を変化させると、それに応じて電場が(電流の増加方向と逆向きに)できてそれが光速で広がる、というのが電磁気の法則の示すところである、ということになります。 -- 前野?
- 大変忙しい中、ご解答いただきありがとうございます。Bの源はjなので、Bを変化させるにはjを変化させないといけない。このjの変化が光速で伝わってい誘導電場をつくるというふうに理解していいのでしょうか。 -- 高校教諭?
- rotE=-dB/dt --
- rotE=-dB/dtの両辺を半径rの円内で面積積分すると右辺はこの円内を貫く磁束の時間変化になります。左辺はストークスの定理を使うと半径r上の電場の線積分になります。これは電磁誘導の法則を示しているのですが、もし円の中心付近のBのみを変化させたとしても、Eの線積分の値が変化してしまうことになります。これはBの変化が直ちに円周上に伝わったことにならないのでしょうか。 -- 高校教諭?
- 電場と磁場は二つ合わせて一つの場のようなものなので、磁場を局所的に変化させつつ電場の方は変えないということはできません。つまり「円の中心付近のBのみを変化させて」ということができるとしたら、外から電場を掛けるような操作が必要になり、「円周上の電場がすぐに変化」とはいきません。前に言いましたように今非常に多忙なので具体的に計算で書けませんが(↑に書いたのがだいたいのお話になります)。とにかく「円周上にすぐ伝わる」ってことが起こらないのです。 -- 前野?
- 具体的にどういう物理現象を起こせば「局所的にBを増加させる」ことができるかを考えてみてください。どんな状況を想定してもそれは結局上のほうに書いた「電流を変化させる」ということになります(磁石を動かすのも、分子電流が動くと考えれば同じ)。そして、その電流の変化が電場を変える現象が光速でしか伝わらないことがわかっているわけです。 -- 前野?
- 丁寧にお答えいただきありがとうございます。疑問が解決しました。 -- 高校教諭?
- 少しだけゆっくり考える時間ができましたので、図で説明しておきます。以下は、大きな2次コイルと、真ん中あたりに小さな1次コイルがあるという状況で、最初は下向きに一様な磁場があるものとします。 -- 前野?
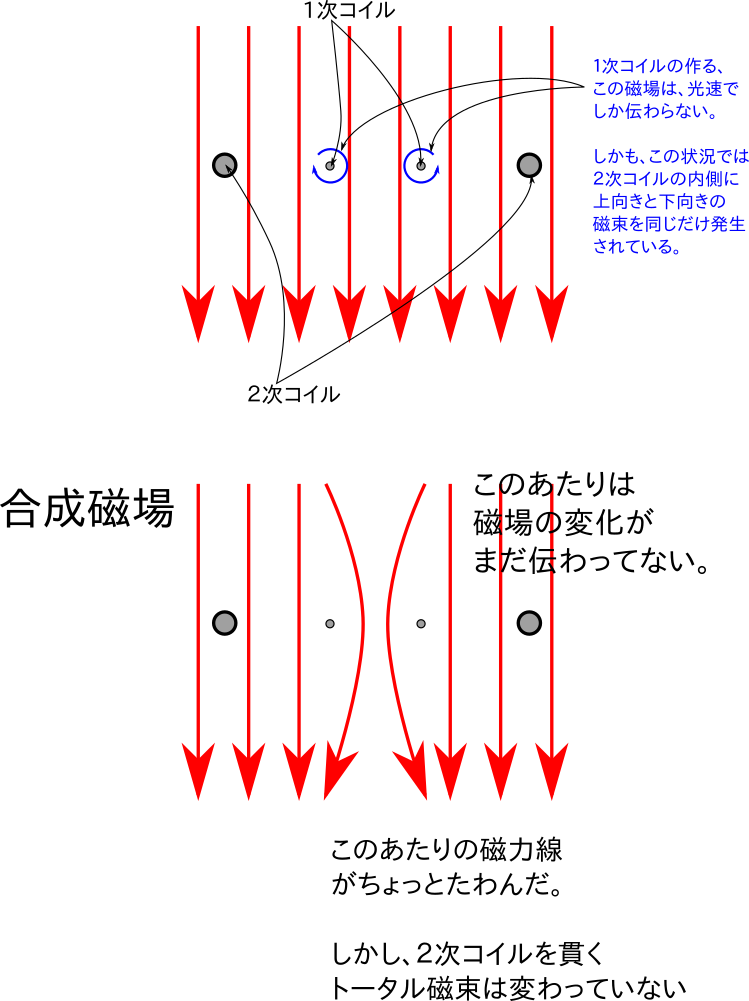
- 小さい1次コイルに電流を流すと磁場が発生し2次コイルを貫く磁束が変化する・・・ように思えますが実は1次コイルが最初に作る磁場は図で青で示したような「くるっ」と回る磁力線なので、磁束はプラマイゼロです。 -- 前野?
- この1次コイルの作る磁力線が外に広がっていって、2次コイルよりも外に出ると初めて「2次コイルと貫く磁束」の量が変化する、ということになります。 -- 前野?
- 大変丁寧に答えていただきありがとうございます。痒い所に手が届く解答に感謝しています。 -- 高校教諭?
![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
![[PukiWiki] [PukiWiki]](image/pukiwiki.png)