
★なかなかおもろい計算
ちょっと現実よりわかりやすく脚色しておりますが。
ある学生さんが、「計算あわないんですけど」と持ってきた計算。要はある作用を$x$で変分してオイラー・ラグランジュ方程式を出す、って計算ですが。
そのラグランジアンを${1\over2}m\left({\mathrm dx\over\mathrm dt}\right)^2$とすると、これを$x$で微分しようとして、${\mathrm dx\over\mathrm dt}$を$t$で微分した後、${\mathrm dt\over\mathrm dx}$をかけるという計算をやったのでした。
五十六億七千万歩ゆずって、これが普通の関数の普通の微分で、$x$と$t$が普通に関係する数なら、まぁ「$t$で微分してから${\mathrm dt\over\mathrm dx}$をかける」ってのは「$x$で微分する」の替りになるじゃん、ってことにはなるんでしょうが、それにしても…。
これ、$t$で微分して$m{\mathrm dx\over\mathrm dt}{\mathrm d^2x\over\mathrm dt^2}$になって、${\mathrm dt\over\mathrm dx}$をかけると$m{\mathrm d^2x\over\mathrm dt^2}$になる、という実に「おしいっ!」と言いたくなる結果となります(でも考え方としてはむちゃくちゃだけどな!)。
もちろん、正しいオイラー・ラグランジュ方程式なら、符号が反対で出てこなきゃいけないのですが(^_^;)。
まぁ、ずっと前にいた、「${\mathrm dx\over\mathrm dt}$を$x$で微分すると、${\mathrm d\over\mathrm dt}$になる」という計算をした人よりは少しましかも。
★WATER CRYSTAL
なるものを近所のスーパー(マルエー)で買ってきた。前にも同様のものを、この日記で紹介したことがあるので一部の人は「またか」と思うかもしれないが、まぁ勘弁して。
こんな袋である↓。

本来は植木鉢などに使用するものだが、要は水をたくさん吸ってくれる(紙おむつなどにも使われている)高分子ポリマーの類であろう。
コップに入れて水をかけて放置すると、
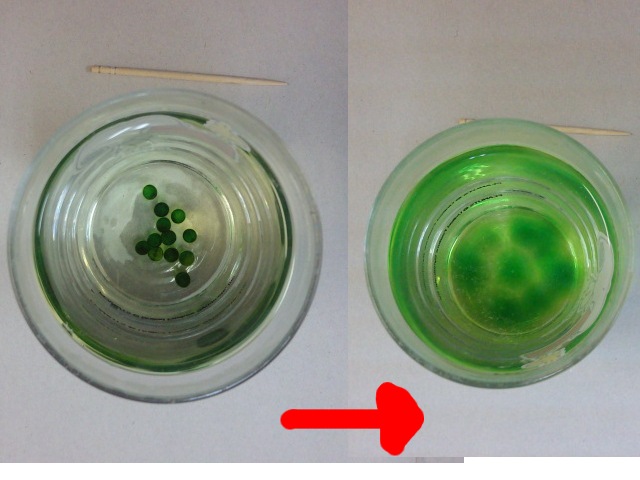
↑こんな感じになる(爪楊枝は大きさ比較用)。水から取り出してみると、

↑こんな感じでものすごく、膨れる。膨れるだけでなく、なんせほとんど水だから水と屈折率もほぼ変わらず、水中に入れるとほぼ見えなくなる。
現状で、こんな感じ↓。

まだ少し見えているが、これは最初から含まれていた緑色の染料(?)がまだ残っているから。もう何度か水を変えているうちにどんどん透明に近づいてきて、「ほら、水と屈折率が同じだと見えなくなるんだよん」というデモンストレーションに使える。




