
★磁束密度はなぜBか?
twitterで「なんで運動量ってpなんだっけ?」と言っている方がいて、
ニュートンは運動量を「impetus」と書いていて、iもmも他でよく使われて混同する文字なので3文字めのpを使ったと言われている。
という話をしました(あちこちに書いてあるので、これはこれであっているはず)。
そこで自分の積年の悩み「どうして磁束密度ってBなの?」を思い出したので、「why magnetic induction B」でぐぐってみると、Answer.comのWhy is B the symbol for magnetic induction?なるページがヒットして、そこには、
When
the magnetic field is observed from the North pole, the magnetic field
emerges and and goes towards south. However, inside a magnet there is
no field at all, thus forming butterfly shape lines. Hence, B stands
for butterfly and due to this concept, scientists used the symbol B for
magnetic induction.
なんて書いてあるんだけど。
磁場は北極から出て南に向かう。しかし磁石内には磁場はない。ゆえに蝶の形を描く。よって蝶々(buttefly)のBだ。
って言うんだけど、ほんとかそれ。しかもこの文章、
- 地球の場合、北極はS極なので、「磁場は南極から出て北へ向かう」じゃないとおかしい。
- div $\vec B$=0なので、磁石中でもBは0ではない。さらにいえば、Hも0ではなく逆向きになっている。
と二つも間違いを含んでいるので、信用できねぇ感がただよってしまう。
同じサイトの、Why do you use the letter b for the magnetic field?には、
Somebody once told me they suspected it was because letters for most other physical quantities had been taken . . .
と書いてあって、「他の文字は他に取られてたから」とあるが、こっちも「Somebody once told…」だからあまり信用できない。しかしま、Aがベクトルポテンシャルに取られたので次のB、というのはなんとなくしっくりこないこともない。
そういえば、「ビオ・サバール」のビオ(Biot)じゃないの?」と誰かが言ってたな。
誰やねん。
★昨日の続報
昨日の吸水ポリマーですが、水を5、6回取り替えた後で、

って感じになってます。もう後何回か水替えがいるな。
★pukiwikiのコメントのspam避け
自分のページのいくつかはpukiwikiを使っているんだけど、その一つである琉球大学理学部准教授・前野昌弘による物理に関する情報の集積所のコメント欄(一番下)に、妙なコメントばっかり書かれるようになった。
たとえば「ukpWKLPKwWjYvM」みたいなまるで圧縮URLのような意味不明の文字列を書いていくのである。
完全に意味不明だから、ブラクラなURLを書かれるのに比べれば害はないのだが、なんか気にいらんし、消すのも手間だ、というわけで、英文字のみの書き込みはシャットアウトするように、pukiwikiのプラグインであるcomment.inc.phpに、
if ($vars['msg'] == '') return array('msg'=>'', 'body'=>''); // Do nothing
// 英文字のみだったらやめる。
if( ereg("[^(a-zA-Z,\.\x20)]",$vars['msg'])==False ) {
return array('msg'=>'', 'body'=>'');
}
$comment = str_replace('$msg', $vars['msg'], PLUGIN_COMMENT_FORMAT_MSG);
というのを付け加えた(付け加えた部分を赤で書いた)。クイックハックもいいところであるが、とりあえずは収まった(これで英文では書き込めないことになるが、まぁあのページに英語でコメントする人はいないだろう、と思う)。
★同じ周の長方形の中で、正方形が面積最大であることを図解するための紙工作
物理の1年生向けの「物理学基礎演習」なる授業の中で、微分の演習とかしているのであるが、その中で、
一周の長さがLの長方形を作り、面積を最大にしたい。面積Sの式を作り、それを微分した式を考察することで「面積が最大になるのは正方形の時である」ことを示せ。
という問題を出している。これは微分の演習問題で簡単にできる。
$S=\left({L\over2}-x\right)x$という式を作って微分して、${\mathrm d S\over \mathrm d
x}= {L\over2} - 2x$となるから(増減表でも書いて)$x={L\over4}$が最大、と言えばよい。
しか〜〜〜し、「計算したらそうなりました」で終るのは物理屋の名折れである。ということで、
また、なぜそうなるのかを図解せよ。
という問題も付け加えている。どうやっていいのかわかりません、と質問を受けたので、以下のような紙細工を持って行って「これ使って説明すること」という課題にした。

例によって裏に磁石をつけて黒板に張れるようにしてある。色塗りが雑なのは、授業中にささっとやったので勘弁して。
6×6=36の正方形になっているわけだが、これの右一列を切り取って
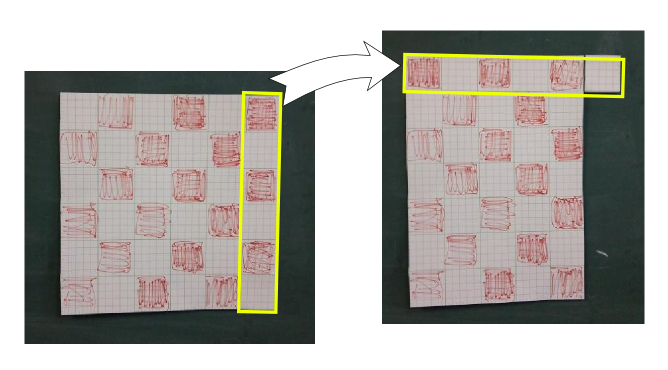
のように並べ直す。これで長方形にすると、

のようになってタイル1個分余ってしまうことがわかる。このタイルが、いわば$\mathrm dS$である。
長方形は5×7=35になるので、この余った部分が「正方形から長方形に(周を変えずに)変形」すると面積が減っちゃうよ、ということを示している。
これで「縦を伸ばすと面積が減る」ということがわかり、この図を90度倒して考えると、「横を伸ばしても面積が減る」ということがわかって、どっちにしろ
正方形の場合が極大だということがわかる。もっとも、これだと「最大」までは言えてないことになるが、縦か横が0になるまで続けても、他に極大になる場所
はないのはすぐわかる。
去年までは図で説明させてたのだが、やはりこういう「手で動かせるもの」の方がずっとわかりやすいようである。
「大学生の授業なのに、小学校みたい」と思う人もいるかもしれない。しかし、「微分して極大を求めて」という計算と、小学生でもできる「正方形がいっちゃんでかい、を図で示す」が、頭んなかでぴったりとつながって欲しい、というのがわしの願いなのである。
←2011年6月前半へ
最新の日記兼更新記録へ 2011年9月後半へ→



