←2012年８月前半へ 最新の日記兼更新記録へ 2012年11月前半へ→
★ちょっと気づいたこと
次の教科書として「よくわかる初等力学」ってのを書いておるのですが。$\vec a\times(\vec b\times\vec c)+\vec b\times(\vec c\times \vec a)+\vec c\times(\vec a\times\vec b)=0$なんて式をどう証明するか、みたいなところを書いていて「おや？」と思ったこと。この式（いわゆるヤコビ恒等式）は平行六面体に働く大気圧の和なんですね。
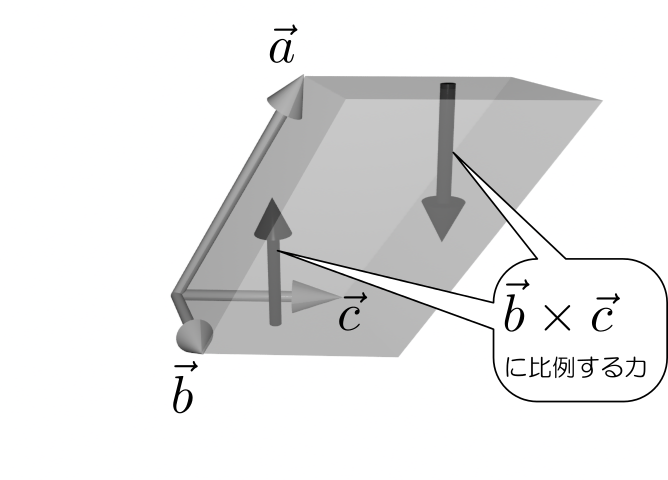
↑こんなふうに３つのベクトルで平行六面体ができていると考えて、ベクトルｂとベクトルｃで作られた面に働く大気圧は（向きも含めて）$\vec b\times\vec c$に比例します。底と天井に２つ逆向きに働いていることを考えるとこれは偶力になっていて、その２つの力の代表点は$\vec a$だけ離れている。こういう場合の偶力の作るトルクは（力の働く点の変位ベクトル）$\times$（力のベクトル）で表せる。だから、この偶力の作るトルクは$\vec a\times(\vec b\times \vec c)$に比例している。これで６つのうち、２つの面についてのトルクを考えたけど、平行六辺形は名前どおり６つの面があるから、同じようなのが都合３つ、a,b,cをサイクリックに回したものが出てくる。そして空気中においておいた平行六面体が勝手に回りだした、なんて話は聞いたことがないから、
$\vec a\times(\vec b\times\vec c)+\vec b\times(\vec c\times \vec a)+\vec c\times(\vec a\times\vec b)=0$
でなくてはならない、というわけ。
説明がけっこう長くなるし、「トルクを受けないから」ってのは証明にはなっていないけど、直感的にこの式が成立していることをわかるにはいいことかもしれない。
ちなみに似たようなことは前にも紹介した「The Mathematical Mechanic: Using Physical Reasoning to Solve Problems」（ちなみに邦訳はこっち）にもあった（もしかしたらこれそのものもあったかもしれない）ので、よく知っている人にはよく知られていることかもしれないけど、自分的には面白かった。
他の式も出せないかな、と思案中。
←2012年８月前半へ 最新の日記兼更新記録へ 2012年11月前半へ→