同様に、$\log{x}$も${x}=0$の回りでは展開できないが、
\begin{equation} {\mathrm d \over \mathrm dx}\log {x} = {1\over {x}},~~{\mathrm d \over \mathrm dx}\left({1\over {x}}\right)=-{1\over {x}^2},~~~ {\mathrm d \over \mathrm dx}\left(-{1\over {x}^2}\right)= {2\over {x}^3},~~~まとめて、{\mathrm d^n \over \mathrm dx^n}\log {x} = (-1)^{n+1} {(n-1)!\over {x}^n} \end{equation}という高階微分を計算したのちに、${x}=1$の回りに展開すれば(テイラー展開の公式にある${1\over n!}$と上で出てきた$(n-1)!$の積で${1\over n}$が残るので)、
\begin{equation} \log {x}= \sum_{n=1}^\infty {(-1)^{n+1}({x}-1)^n\over n}= ({x}-1)-{({x}-1)^2\over 2}+{({x}-1)^3\over 3}-{({x}-1)^4\over 4}+\cdots \end{equation}のような展開ができる。なお、この式を${x}\to 1+{x}$と置き直せば、
\begin{equation} \log (1+{x})= \sum_{n=1}^\infty {(-1)^{n+1}{x}^n\over n}= {x}-{{x}^2\over 2}+{{x}^3\over 3}-{{x}^4\over 4}+\cdots \end{equation}となり、前に出した近似式が出てくる。
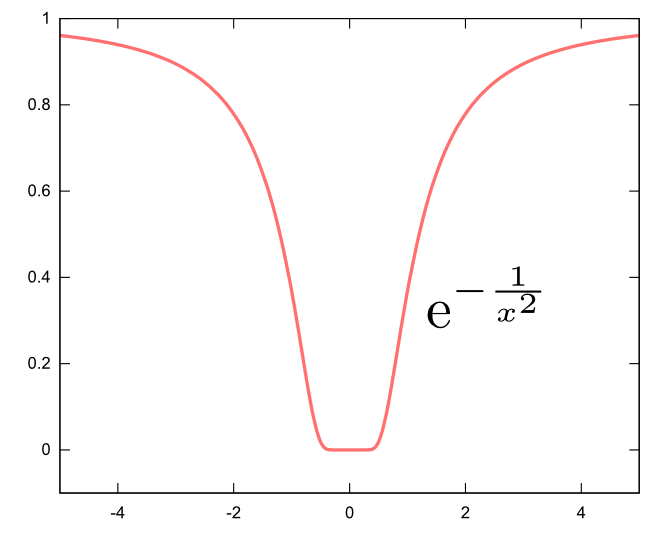
$f({x})=\mathrm e^{-{1\over {x}^2}}$という関数を考えよう。この関数は${x}=0$での値は定義されていないが、グラフに書いたように、${x}=0$の付近では$0$に近づく($\mathrm e^{-\infty}$だと思えばよい)ので、$f(0)=0$と定義しておくことにすれば${x}=0$でも定義された連続した関数になる。
さらに、グラフで${x}=0$付近が水平線になっていることからわかるように、$n$階微分しても${\mathrm d ^n\over \mathrm dx^n }f(0)=0$である。一階微分と二階微分だけ計算しておくと、
\begin{equation} {\mathrm d \over \mathrm dx}f({x})={2\over {x}^3}\mathrm e^{-{1\over {x}^2}},~~ {\mathrm d^2 \over \mathrm dx^2}f({x})= -{6\over {x}^4}\mathrm e^{-{1\over {x}^2}} +{4\over {x}^6}\mathrm e^{-{1\over {x}^2}},\cdots \end{equation}のようになるが、${x}=0$に近づけると$\mathrm e^{-{1\over {x}^2}}$が非常に早く0に近づくので、これらはすべて0となる。よって、右辺が恒等的に(${x}$によらず)0になってしまう。
←√のテイラー展開のページへ ↑第11講の最初へ 受講者の感想・コメントのページへ→