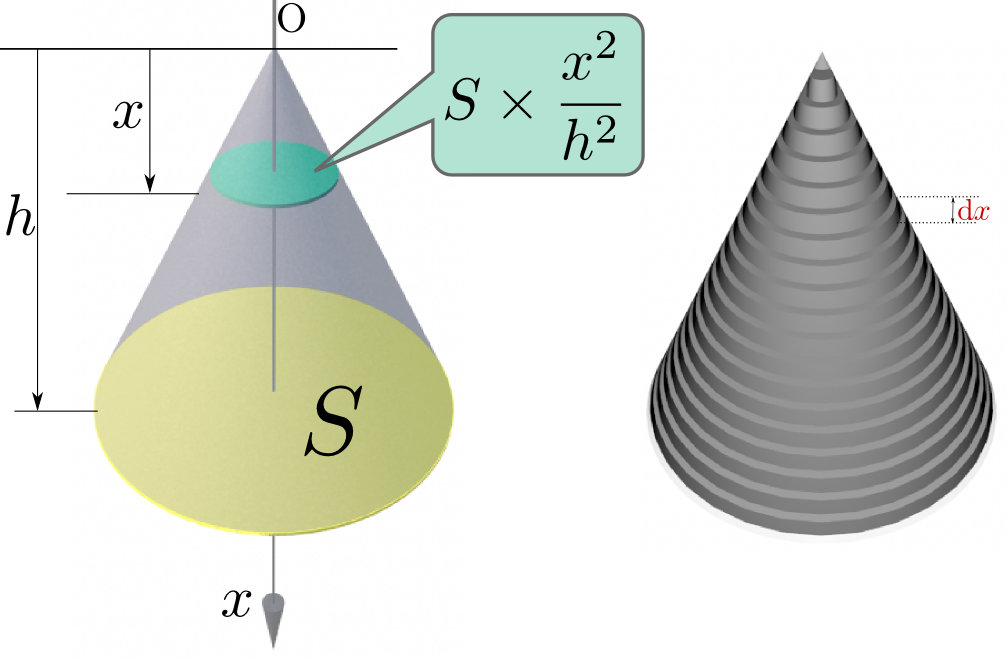
円錐や角錐の体積は底面積を$S$、高さを$h$とすると、${1\over 3}Sh$で書ける。これを定積分を使って出そう。

頂点を原点として、底面に垂直な方向の距離を考えて、その距離${x}$とする(面に垂直な下向きの方向に${x}$軸を取る)。
そして定積分の精神に従って、この${x}$を微小区間に切り刻み、その一つの微小区間の幅(この円錐や角錐をビルと考えた時の「一階の高さ」である)を$\mathrm dx$とする(座標${x}$から座標${x}+\mathrm dx$までを切り取って考える)。
この一階の体積は、この階の底面積$\times \mathrm dx$である。面積はスケールの自乗に比例するから、底面積は$S\times{{x}^2\over h^2}$である(右の図では円錐の場合を示したが、角錐であっても同様)から、
\begin{equation} \int_0^h {S{x}^2\over h^2}\mathrm dx =\left[{S{x}^3\over 3h^2}\right]_0^h={Sh\over 3} \end{equation}となる。分母の3の出処は$\int_a^b{x}^2\mathrm dx=\left[{{x}^3\over 3}\right]_a^b$の3だったのである。

ここで体積を計算した方法からすると、円錐や角錐の頂点が(底面に平行な方向に)移動したとしても体積が変わらない(つまり体積は底面積と高さだけで決まり、傾きにはよらない)ことが納得できる。これは円柱などの場合でも同じである。
球も同様に微小な高さ$\mathrm dx$に分けて考える。

今度は${x}=0$は球の中心におくと、図に描いたように、各階の床は半径$\sqrt{r^2-{x}^2}$の円で、底面積$\pi(r^2-{x}^2)$を持つ。これに高さ$\mathrm dx$を掛ければ一階分の体積が出るから、範囲$-r < x < r$でこれを積分して、
\begin{equation} \int_{-r}^r \pi(r^2-{x}^2)\mathrm dx=\pi\left[r^2 {x}-{{x}^3\over 3}\right]_{-r}^r=\pi\left( r^3-{r^3\over 3}-\left(-r^3 + {r^3\over 3}\right)\right)={4\pi r^3\over 3} \end{equation}となる。
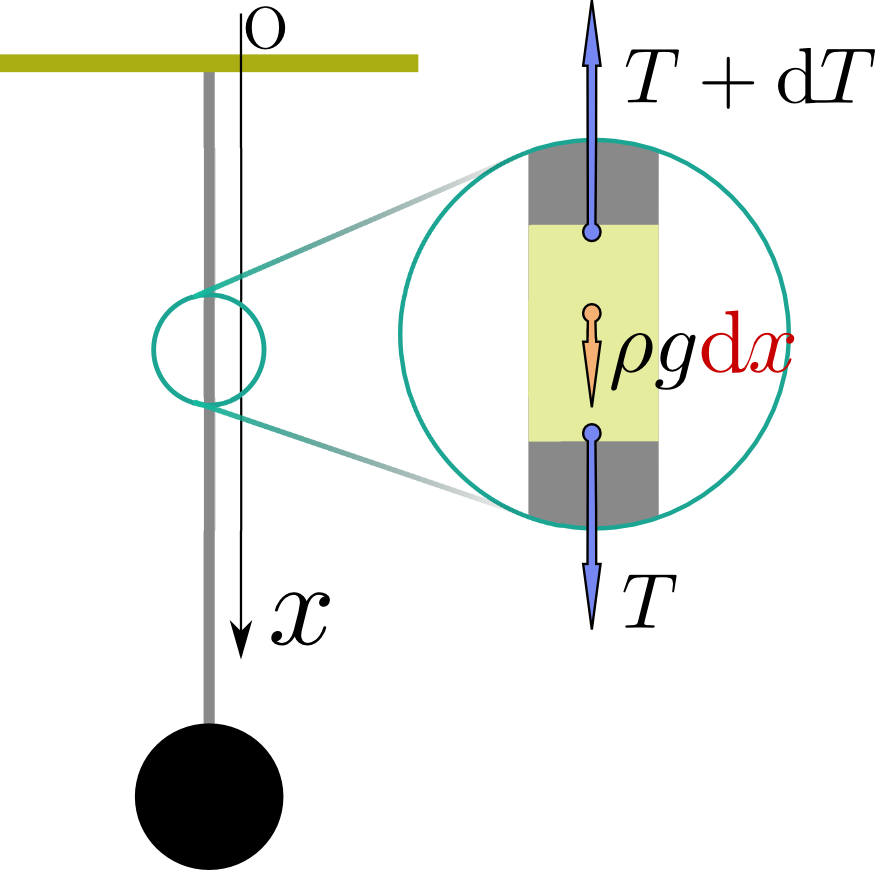
質量$m$の物体を天井から長さ$\ell$の糸で吊るす(糸は伸びないとする)。糸が単位長さあたり$\rho$の質量があるとすると、天井から${x}$の位置での張力はどれだけか、という問題を考えてみる。やはり糸を$\mathrm dx$という微小部分ごとに切ろう。その微小部分の質量は$\rho \mathrm dx$であり、ここに働く力は、重力$\rho g\mathrm dx $と、上の部分の糸の張力$T$と下の部分の糸の張力$T+\mathrm dT$である(下の部分では張力が変化していることに注意)。つりあいの式は
\begin{equation} \rho g \mathrm dx + T+\mathrm dT = T \end{equation}であるから、
\begin{equation} \mathrm dT = -\rho g \mathrm dx \end{equation}積分して、
\begin{equation} T= -\rho g x + C \end{equation}となる。糸の端で$T=mg$となるから、
\begin{equation} mg = -\rho g \ell+C \end{equation}となって、
\begin{equation} T= \rho g (\ell-x)+ mg \end{equation}とすれば任意の場所での張力が計算できる(実はこれは次の章からやる微分方程式の、もっとも簡単な例である)。
この結果は積分なんて使わなくても、図のように糸を場所$x$で(頭の中だけで)切断して、切断した場所より下にある部分の質量が$m+\rho(\ell-g)$であることを考えればわかる。

そこで次に積分が必要な状況を考えよう。簡単のため重力のない無重力空間を考えて、物体をある点を中心にくるくる回したとする(その回転の角速度を$\omega$としよう)。物体とともに運動している系で考えると、中心から$x$の場所の微小部分には、遠心力$\rho x\omega^2 \mathrm dx$が働いているから、この場合のつりあいの式は
\begin{equation} \rho {x}\omega^2 \mathrm dx + T+\mathrm dT = T \end{equation}であり、これを積分していくと、
\begin{equation} T= -{\rho\omega^2\over 2} x^2+C \end{equation} となる。この場合は$x=\ell$のところで$T=m\ell\omega^2$となることを使って積分定数を定め、 \begin{equation} T= m\ell\omega^2 + {\rho\omega^2\over 2}(\ell^2-x^2) \end{equation} が答えとなる。もっとも単純な微分方程式は
\begin{equation} {\mathrm d \over \mathrm dx} f({x})=0\label{DEzero} \end{equation}である。これは計算するまでもなく「微分して0になるのは定数」と判断して、
\begin{equation} f({x})=C\label{DEzerosol} \end{equation}が解となる。これは二つ上の式を積分した結果が上の式だと考えても同じことである。
この、もっとも簡単な微分方程式も、微分方程式の解は、微分方程式だけでは決まらないという一般的性質を持っている。「決まらない」理由は積分定数という任意の定数が入ってくるからであると考えておけばよい。あるいは、微分が決まるということは「その点での傾き」が決まるだけであるから、「どの点で始めるか」を決めないことには線が引けない(関数が決まらない)と考えてもよい。
次に、もう何度も出てきている例を考えよう。
\begin{equation} {\mathrm d \over \mathrm dx} f({x})=f({x})\label{dfdxf} \end{equation}も微分方程式である(関数$f({x})$とその導関数${\mathrm d \over \mathrm dx}f({x})$とで作られた方程式である)。
この解(の、少なくとも一つ)を、我々はとっくに知っていて、
\begin{equation} f({x})=\mathrm e^{{x}}\label{solex} \end{equation}がその答えである。ただし、これは「一つの解」ではあるが「全ての解」ではない(上に書いたように微分方程式の解は、微分方程式だけでは決まらないのである)。
実際、この微分方程式をよく見ると、$\mathrm e^{{x}}$に定数$A$を掛けた$A\mathrm e^{{x}}$もまた、微分方程式を満たすことがわかる。それは、両辺が$f({x})$の1次式であることからもわかる。一般に、微分方程式が求めるべき関数$f({x})$に関して同次(1次なら1次ばかり、2次なら2次ばかりを含んでいる)ならば、定数倍しても解である。
ということは、
\begin{equation} f({x})=A\mathrm e^{{x}} \end{equation}と書くことができる。この解は「一般解」である。
一般解はたくさん($A$の数だけだから実際無限個)ある。つまり微分方程式だけでは、解を一つに定めることはできない。解を一つに定める時には、なんらかの付加的な条件を置く。たとえば「$f(0)=1$とする」のように(この場合$A=1$となる)。
このような条件は状況に応じて「境界条件(boundary condition)」あるいは「初期条件(initial condition)」などと呼ばれる条件を定める場所が時間的な「最初」である時は「初期条件」という言葉がよく選ばれる。。
このような方程式に従う自然現象の例としては、放射性物質の崩壊がある。放射性物質は、「半減期」と呼ばれる一定期間(以下$T$とする)を経過すると元の量のうち半分が崩壊注意すべきは「半減期の2倍」の時間が経過すると全部なくなるのではなく、元の量の${1\over 4}$になる、ということ。し、別の物質に変化する。よって、時刻$t$における放射性物質の量$N(t)$は
\begin{equation} N(t)=N(0)\left({1\over 2}\right)^{t\over T} =N(0)\mathrm e^{-{t\log 2\over T}}\label{hangenki} \end{equation}という式で表すことができる。なぜこのような式になるのかというと、上の式が微分方程式の解であることとわかるように、
\begin{equation} {\mathrm d \over \mathrm dt}N(t)=-{\log2\over T} N(t) ~~または~~ \mathrm dN=-{\log2\over T}N \mathrm dt \end{equation}という式が成立しているからである。この式の意味は、微小時間$\mathrm dt$の間に放射性物質の量が$-{\log 2\over T}\mathrm dt$だけ減るということである。$N,\mathrm dt$以外の量は定数なので、「今ある量に比例して減る」という法則を示している。これは放射性物質はまわりの状況や物質の状態とは無関係に一定確率で崩壊するということを示している。これが生物の死であれば「年老いた個体は死にやすい」「密集した環境では食料が確保できず死にやすい」などの理由で確率が変わる。放射性物質には「年齢」のような個性がないということがわかる。
微分方程式を解くテクニックは解くべき微分方程式の形により様々なので、後のために微分方程式の形を分類しておこう。
微分方程式は、独立変数${x}$、従属変数${y}$と、その微分${\mathrm d \over \mathrm dx}{y},{\mathrm d ^2\over \mathrm dx^2}{y},\cdots$の間にある
\begin{equation} \Phi({x},{y},{\mathrm d \over \mathrm dx}{y},{\mathrm d ^2\over \mathrm dx^2}{y},\cdots)=0 \end{equation}のような形で書ける関係式であり、この式を満たす${y}$と${x}$という関係を求める、というのがその目的である。
微分方程式を分類する方法の一つが「何階微分を含むか」という点での分類である。$n$階以下の導関数を含む微分方程式を「$n$階微分方程式」と呼ぶ。
\begin{equation} \Phi({x},{y},{\mathrm dy\over \mathrm dx})=0 \end{equation}となるのが一階微分方程式である。$n$階の微分方程式を解くということは不定積分を$n$回やるから、不定積分のたびに積分定数が出て来て、$n$個の「未定のパラメータ」を含む。つまり$n$階微分方程式の解は$n$個の(微分方程式だけでは決まらない)パラメータを含むと考えてよい(ただし、微分が不連続性を持つ関数では、積分定数が領域によって違うということもあるので、その場合パラメータの数は増える)。
一階微分方程式を適当に変形することで、
\begin{equation} {\mathrm d\over\mathrm dx}{y}=F({x},{y}) \end{equation}の形にできた時、この式は正規形である、と言う。右辺が定まらない場合は非正規形である。一例を挙げると
\begin{equation} \left({\mathrm d\over\mathrm dx}{y}\right)^2+{y}^2 = 1 \end{equation}で、これを変形しても、
\begin{equation} {\mathrm d\over\mathrm dx}{y}=\pm\sqrt{1-{y}^2} \end{equation}となってしまって${\mathrm d\over\mathrm dx}{y}$が一つに決まらない。
微分方程式を使って求めたい関数を${y}$とした時、微分方程式が${y}$に対して線型(つまり定数と${y}$の1次式しか含んでいない場合)を「線型微分方程式」と呼ぶ。線型の微分方程式は
\begin{equation} A{\mathrm d ^2 \over \mathrm dx^2}{y}+B {\mathrm d \over \mathrm dx}{y} +C {y}+D=0\label{senkeiy} \end{equation}のような形をしている(${y}$の微分についても線型であることに注意)。この式は${y}$の線型二階微分方程式ということになる(一階もしくは三階以上の微分方程式も同様に考えられる)。
この式は$D$という「定数項」を含んでいるが、これを含まない場合(つまり$D=0$の場合)は(次数がそろっているという意味で)「斉次線型微分方程式」と呼ぶ($D\neq0$の時は「非斉次線型微分方程式」である)。
そしてもう一つ、重要な分類が次の節で行う「変数分離」が可能かどうかである。
以下では、微分方程式の中でも比較的簡単(でも応用範囲は広い)な「変数分離できる微分方程式」について考えていこう。
タイトルにある「変数分離できる」とは、「微分方程式を変形することで、
\begin{equation} f({y})\mathrm dy = g({x})\mathrm dx\label{hensuubunri} \end{equation}の形にすることができる」ということである。変数分離される前は、$ {\mathrm dy\over \mathrm dx}({x})={g({x})\over f({y})} $という形である。つまりは${x}$と${y}$という二つの変数が左辺と右辺に分離できる場合を考える。
\節{DEexp}で例として上げた$ {\mathrm d \over \mathrm dx} f({x})=f({x})$は変数分離できる微分方程式の例でもある。
\begin{equation} \begin{array}{rl} {\mathrm dy \over \mathrm dx}=&{y} \\ {\mathrm dy \over {y}}=&\mathrm dx\\ \log|{y}|=&{x}+C \end{array} \end{equation}のように、「変数分離した後で積分」という方法で解くことができる。
FAQ:左辺には積分定数はいらないのですか?
左辺に積分定数をつけても、結果は同じなのである。もし左辺に積分定数をつけたとすれば、左辺の積分定数と右辺の積分定数は別の定数なのでそれをそれぞれ$A,B$として時々、積分定数をどっちも$C$にして$ {{y}^2\over 2}+C={{x}^2\over 2}+C$として両辺で打ち消してしまう、という計算をする人がいる(←ここは驚くか笑うかするところ)が、積分定数は左辺と右辺それぞれにおいて「任意の数」だから、両辺で一致する理由はない。、
\begin{equation} \begin{array}{rl} {{y}^2\over 2}+A=&-{{x}^2\over 2}+B\\[3mm] {{y}^2\over 2}=&-{{x}^2\over 2}+B-A \end{array} \end{equation}となるが、$A$も$B$もまだ決まっていない数であり、しかも結果には$B-A$という組み合わせでしか出てこない。つまり、答えを出すためには$A,B$それぞれを求める必要はなく、$B-A$だけを求めればよいから、$C=B-A$とおいて1つの積分定数と思えばよい。
簡単な例を示そう。
\begin{equation} {\mathrm dy\over \mathrm dx}=-{{x}\over {y}} \end{equation}という式(前に図で考えた微分方程式で、答は円であった)は書き直すと
\begin{equation} {y}\mathrm dy = -{x} \mathrm dx \end{equation}と変数分離できる。これを積分すると、
\begin{equation} \begin{array}{rl} \int {y}\mathrm dy =& -\int{x} \mathrm dx\\[3mm] {{y}^2\over 2}=&-{{x}^2\over 2}+C \end{array} \end{equation}となる。$C$は積分定数である。
結果を整理すると、
\begin{equation} {x}^2 +{y}^2 = 2C \end{equation}という円の式が出てくる(半径は$\sqrt{2C}$である)。
次に${\mathrm dy\over \mathrm dx}={{y}\over {x}}$を同様に解いてみよう(\reftext{chokusendiff}{図で考えた時}、この解は「原点を通る直線」であった)。
\begin{equation} \begin{array}{rll} {\mathrm dy\over \mathrm dx}=&{{y}\over {x}}&変数分離\\ {\mathrm dy\over {y}}=&{\mathrm dx\over {x}}&積分\\ \log {y} =& \log {x} +C&{両辺を\mathrm e の肩へ}\\ {y}=& {x}\mathrm e^C \end{array} \end{equation}となり、確かにこれは(傾き$\mathrm e^C$の)直線である(図を描いて考える方が直線という答がすっとわかる)。
燃料を噴射して飛ぶロケットの噴射した燃料の量と到達速度の関係は微分方程式から求めることができる。もし、我々が微分方程式というものを知らないとすると、以下のような「大間違い」をやらかすことになる。
大間違い
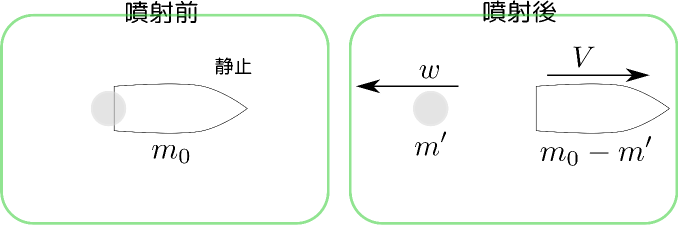
静止していた質量$m_0$のロケットが質量$m'$の推進剤(燃料を燃焼させた結果であるガスなど)を速さ$w$で後方に噴射した。噴射後、ロケットが速さ$V$になったとする。運動量の保存から、
\begin{equation} 0=(m_0-m')V +m'\times (-w) \end{equation}が成り立つ。
結果として、$V={m'\over m_0-m'}w$である。
上の「大間違い」は何が間違いなのかというと、ロケットの質量も速度も連続的に少しずつ変化していく量なのに、まるで一気に変わったかのように考えてしまったことである。連続的に少しずつ変化していく量は微分や積分を使って表現しなくてはいけない。そこで、微小変化について絵を描くと以下のようになる。

左の図はすでにある程度噴射した途中の状態で、すでに速度$V$を持っている。この時の質量は最初の$m_0$に比べて少ない$m$になっている。その微小時間後に、ロケットは質量$m+\mathrm d m$で速度$V+\mathrm dV$になっている。噴射された推進剤は「大間違い」の図のように$w$の速度で後方へ進むのではなく、$V-w$という速度で前方へ進む($w>V$ならば$w-V$の速さで後方へ進む)。既に速度$V$を持っているロケットから、$w$の速さで後方に噴射されたのだから、$w$ではなく速さ$w-V$になる、と考えればよい。
ここで、$\mathrm d m$は「質量の変化量」であるから、今質量が減っていくという状況においては負の量であることに注意しよう---だからといって気を利かせたつもりで、噴射後の質量を$m-\mathrm d m$とかやってはいけない(よくある間違いである)。$\mathrm d m$など$\mathrm d $のついた量はあくまで「変化量」であり、減る時は$\mathrm d m<0$であると考えていかないと、積分結果がおかしなことなってしまう。よって、噴射された推進剤は質量が$-\mathrm d m>0$なのである。
運動量保存則を考えると、
\begin{equation} m V = (m+\mathrm d m)(V+\mathrm dV) -\mathrm d m (V-w) \end{equation}となる。この式を整理すると、
\begin{equation} \begin{array}{rl} \underbrace{mV}_{相殺→}=&\underbrace{mV}_{←相殺} + \underbrace{\mathrm d m V}_{相殺→}+ m\mathrm dV +\underbrace{\mathrm d m \mathrm dV}_{高次の微小量} \underbrace{-\mathrm d m V}_{←相殺}+ \mathrm d m w \\ -m\mathrm dV=& \mathrm d m w \\ \mathrm dV=& -w {\mathrm d m \over m} \end{array} \end{equation}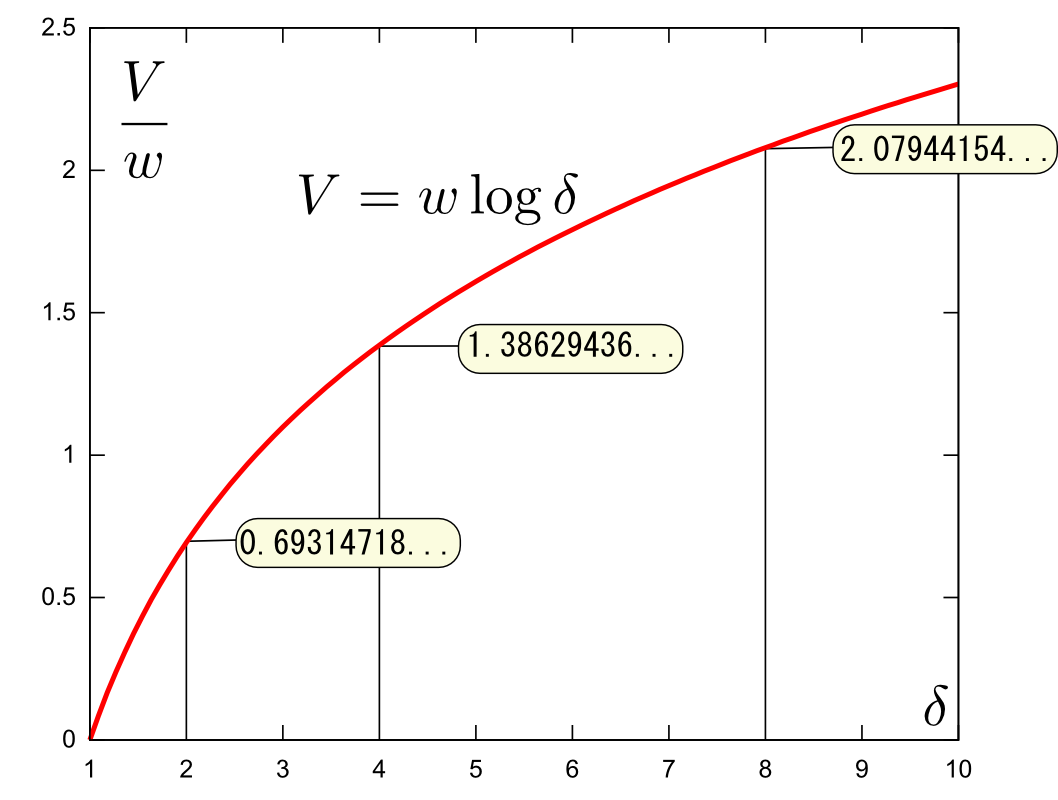
となる。この積分結果は$V=-w\log m +C$である。$m=m_0$(初期値)の時に$V=0$という初期条件を使うと、$C=w\log m_0$となるので、
\begin{equation} V=-w\log m+w\log m_0= w\log\left({m_0\over m}\right) \end{equation}が成立する式となる。$\delta=\left({m_0\over m}\right)$という量は「質量比」と呼ばれる(文字通り、噴射前と噴射後の質量の比である)。グラフで分かるように、$\delta$を大きくしても$V$はどんどん増えるというわけにはいかない($\log x$という関数は傾き${1\over x}$だから、傾きがどんどん緩くなっていく)。ロケットの性能を上げるには$w$を大きくすることが大事であることがわかる。