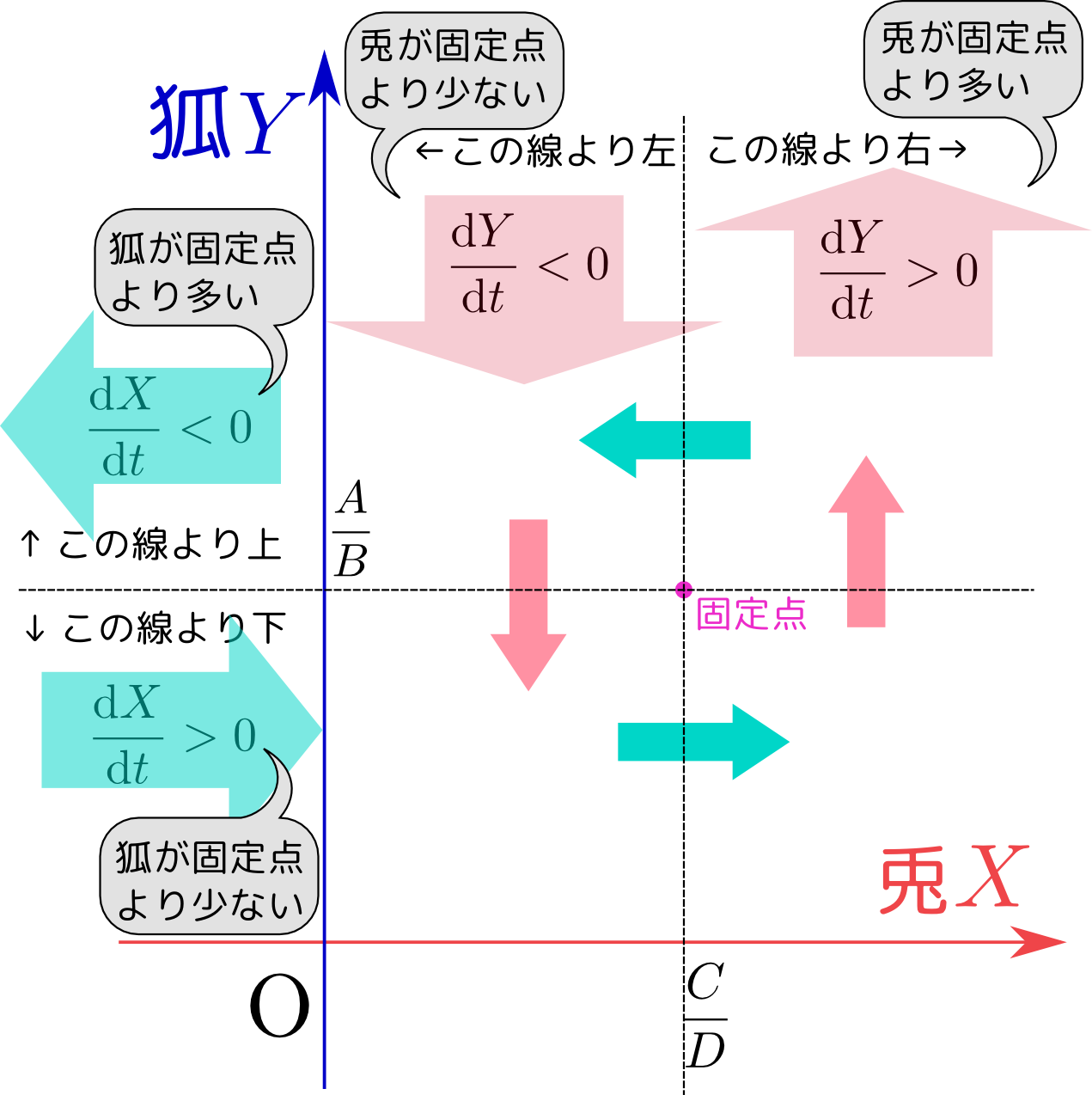
懸垂線
紐を2点を固定してつりさげた時の形を考えてみる。


一番下の部分を原点として、下の図のように座標系を張る。
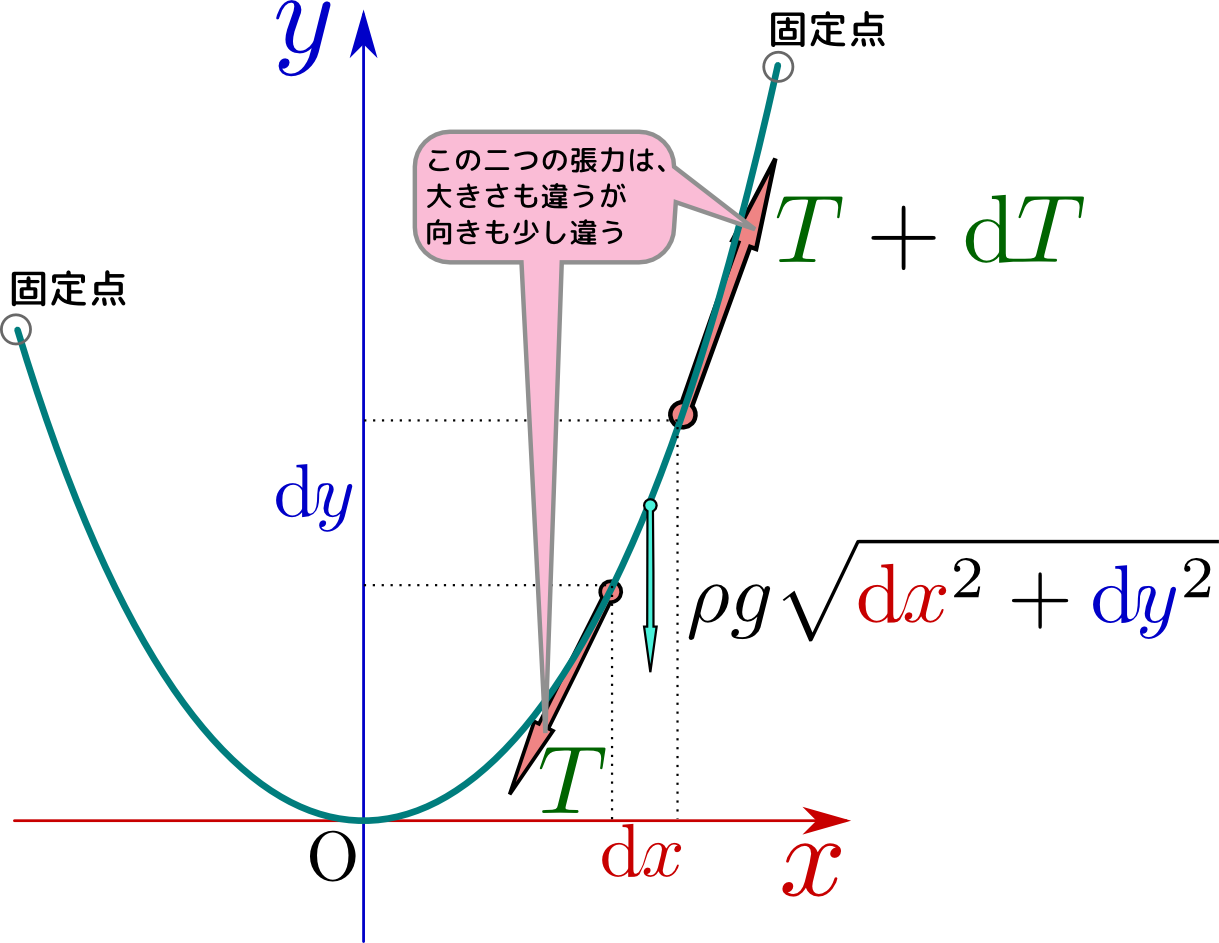
紐にか\かる張力は(垂直に垂らした時と同様に、上の方ほど大きくなるはずだから、図のように微小部分を考えた時、下端には${T}$、上端には${T}+\mathrm dt$の力が働く。紐は直線状ではないからこの張力の向きも(微小に)違う。働く力はこの他に重力がある。微小部分の紐の長さは$\sqrt{\mathrm dx^2+\mathrm dy^2}$だから、これに単位長さあたりの質量$\rho$と重力加速度$g$を掛けた分の重力が下向きに働く。
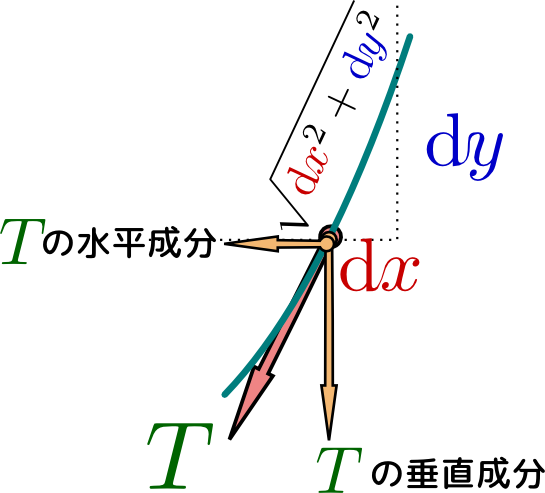
この微小部分に働く張力の水平成分は等しいはずである。よって、
\begin{equation} {T}{\mathrm dx\over \sqrt{\mathrm dx^2+\mathrm dy^2}}=T_0~~~(T_0は定数)\label{suiheiteisuu} \end{equation}が成り立つ。ここで$T_0$は、$\mathrm dy=0$の時の張力だと思えばよい(図を見ると、それは最下点すなわち原点である)。
次に垂直成分を考えると、${T}$の垂直成分の増加がちょうど重力によって打ち消されればつりあいが保たれるから、「${T}$の垂直成分の微分」が、その微小部分にかかる重力に等しくなる。式で表現すれば、
\begin{equation} \mathrm d \left( {T}{\mathrm dy\over \sqrt{\mathrm dx^2+\mathrm dy^2}} \right)=\rho g \sqrt{\mathrm dx^2+\mathrm dy^2} \end{equation}が成り立つということである。
上の式から、${T}=T_0{\sqrt{\mathrm dx^2+\mathrm dy^2}\over \mathrm dx}$として代入して、
\begin{equation} \mathrm d \left( T_0{\mathrm dy\over \mathrm dx} \right)=\rho g \sqrt{\mathrm dx^2+\mathrm dy^2} \end{equation}となる。$T_0$は定数だから微分の外に出して、右辺は$\mathrm dx$をルートの外に出し、
\begin{equation} T_0\mathrm d \left({\mathrm dy\over \mathrm dx}\right)=\rho g\sqrt{1+\left({\mathrm dy\over \mathrm dx}\right)^2}\mathrm dx \end{equation}とした上で、${\mathrm dy\over \mathrm dx}=V$と考えれば
\begin{equation} \mathrm dV= {\rho g\over T_0}\sqrt{1+V^2}\mathrm dx \end{equation}という変数分離可能な微分方程式になる。$\sqrt{1+V^2}$という形が出てきたので、$V=\sinh {t}$という置換積分($\mathrm dV=\cosh {t} \mathrm dt$となる)を使って計算して、
\begin{equation} \begin{array}{rll} {\mathrm dV\over \sqrt{1+V^2}}=&{\rho g\over T_0}\mathrm dx &{V=\sinh {t}として} \\ {\cosh {t} \mathrm dt\over \cosh {t}}=&{\rho g\over T_0}\mathrm dx &{積分して} \\ {t}=&{\rho g\over T_0}x+C~~~&(Cは積分定数) \end{array} \end{equation}であるから、
\begin{equation} V={\mathrm dy\over \mathrm dx}= \sinh \left({\rho g\over T_0}x+C\right) \end{equation}となる。これをさらに積分して、
\begin{equation} y= {T_0\over \rho g}\cosh \left({\rho g\over T_0}x+C\right)+D~~~(Dは積分定数) \end{equation}が解となる。最初に図で設定したように$x=0$で$y=0,{\mathrm dy\over \mathrm dx}=0$とすれば、$C=0,D={-{T_0\over \rho g}}$となり、最終的な答えは
\begin{equation} y= {T_0\over \rho g}\left( \cosh \left({\rho g\over T_0}x\right)-1\right)\label{kensui} \end{equation}となる。このような曲線($\cosh$で表される)を「懸垂線」と呼ぶ。最初「放物線?」と思った人がいたが、計算結果は$\cosh$である。しかし
\begin{equation} \cosh x =1+{1\over 2}x^2 + {1\over 24}x^4+\cdots \end{equation}という展開であることを考えると、$x$が小さい範囲ではこの式は$y=ax^2$とほぼ同じである。